Probability Activity with Cuboctahedrons

My statistics class recently did a data collection activity related to probability with cuboctahedrons.

Due to the Thanksgiving holiday, we only had two days of school this week.  Needless to say, my students were not very excited about having to come to school on Monday and Tuesday.  Several of the schools around us took the entire week off, so that made the week seem even more torturous to my students.

My statistics students were especially restless.  We’re in the middle of our unit on probability.  Monday, we looked at some probability word problems.  On Tuesday, I wanted to do something fun and interesting but still related to probability.  I did a quick google search of probability activities, and I ran across a net of a cuboctahedron.  Isn’t that just a fun word?  Cuboctahedron.  Cuboctahedron.  Cuboctahedron.  It just makes me smile.

The activity from the MEP Demonstration Project instructed students to assemble their own cuboctahedron.  (The net is on page 4 of the linked PDF document.) Then, they were to toss the cuboctahedron 100 times and count how many times it landed on a square face and how many times it landed on a triangular face.

I let my students each pick a sheet of card stock from the cabinet, and I quickly ran off nets for them to cut out and assemble.  The cutting and gluing process was more time intensive than I realized.  This activity took the entire 50-minute period.  Since it was the day before Thanksgiving break, this was perfectly fine.  Most of my students ended up opting for tape because the net was so hard to put together.  I used glue, and it works fine if you have enough patience to let the glue dry a little between steps.

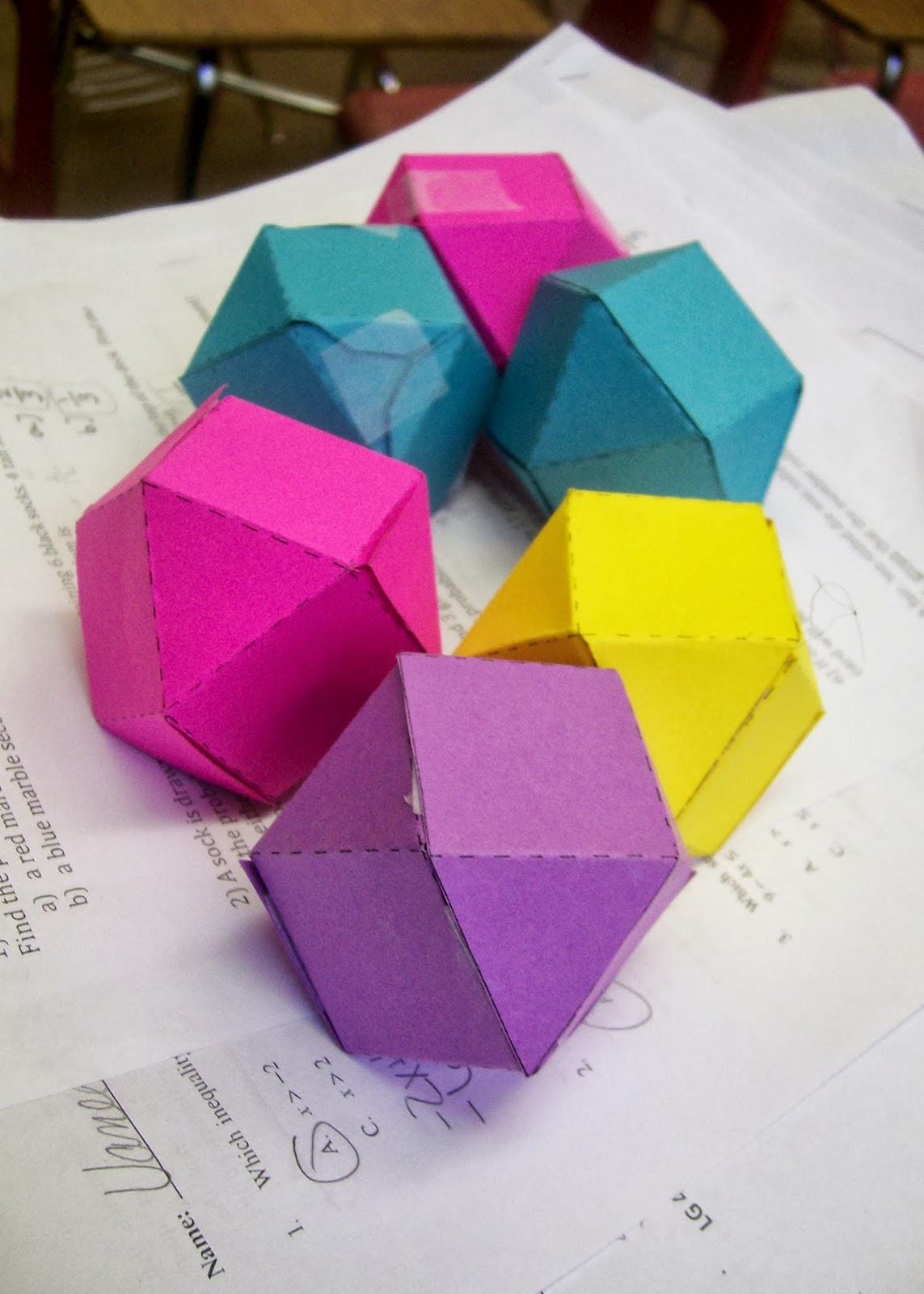
The cuboctahedron consists of 6 square faces and 8 triangular faces.  Students were asked to predict the probability that the cuboctahedron would land on each type of face BEFORE tossing it 100 times.

As a class, they decided that 6/14 of the faces were squares.  Therefore, the probability of landing on a square face was approximately 0.43.  8/14 of the faces were triangles.  Thus, the probability of landing on a triangular face was approximately 0.57.  ‘

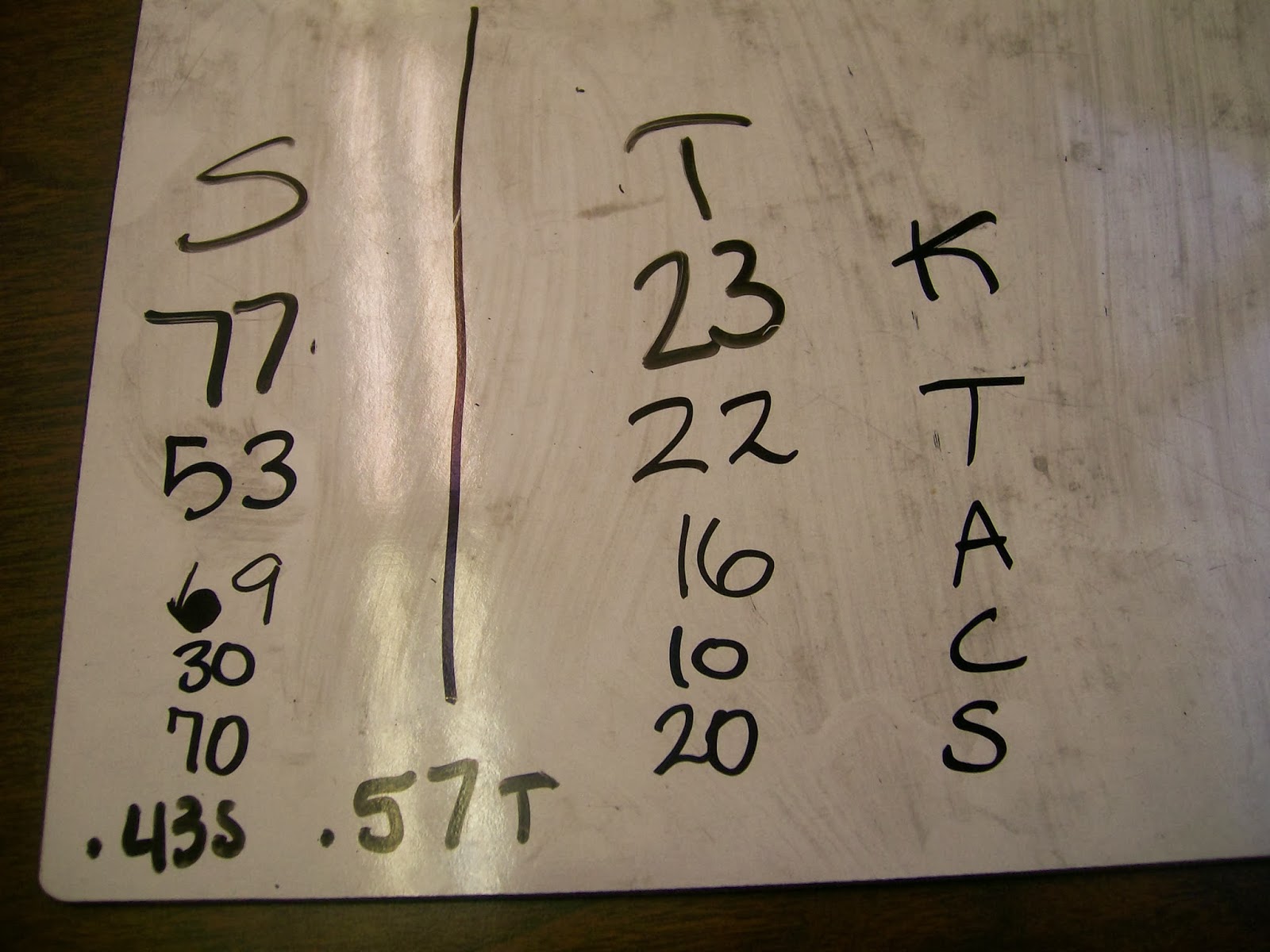
In 299 trials, the cuboctahedron landed on a square face.  In 91 trials, the cuboctahedron landed on a triangular face.  So, the experimental probability of landing on a square face was approximately 0.77, and the experimental probability of landing on a triangular face was approximately 0.23.

My students were intrigued by this data.  I’m not sure what the authors’ motivation was in writing this activity.  Were we supposed to get these surprising results?  We had a discussion of the difference between theoretical and experimental probability.  What is the reason behind this discrepancy?  Is it related to the differing areas of the faces?  Or, is it as one student suggested related to the way that the cuboctahedron lands?  It often hits on a corner, and when this happens it almost always favors the square faces for landing.

I liked this activity because it got my students thinking and talking about math on a day when they didn’t feel like doing any math.  It’s a rare thing when I give my students a problem I don’t already know the answer to.  I need to do this more often!  Does anyone know more about this perplexing polyhedron probability problem?