Level the Towers Activity for Introducing Mean

Recently, I’ve been trying to find a way to organize many of the amazing resources I’ve found online so I can use them more easily in the future.  Don Steward’s blog is an absolute treasure trove of activities and interesting problems for any mathematics classroom.  

A few weeks ago, I went through every single one of his blog posts and took note of all of the activities that aligned with my Algebra 1 standards.  There were A LOT of them!

One of the activities that caught my eye was called “Equal Sharing.”  Students are given a set of towers and asked to make all of the towers have the same height.  You must maintain the same number of towers.  The only thing you can change is the arrangement of the blocks.

I took Don’s activity sheet that featured 10 problems, stuck it in a publisher file, enlarged it to fit on 11″ x 17″ paper, and added a title with a cute font.  I printed the puzzle on some 11 x 17 cardstock that is amazing for creating activities that can easily be worked on by multiple students at the same time.  It also makes pretty awesome posters!

Then, I stuck each activity into one of my new 11 x 17 dry erase pockets to make the activity reusable.

If you are looking to save a bit of money, you can also pick up a package of 11 x 17 sheet protectors for a much cheaper price! They won’t be quite as durable, but students can still write and erase with their dry erase markers.

I allowed students to work on this activity in groups of 2 or 3.  A few of my students chose to work alone.  The majority of students were in pairs.

I didn’t give them many details before I let them loose.  I instructed them that their challenge was to rearrange the blocks so that each tower was the same height.  They had to end with the same number of towers that they started with.

Even though I told students before we started that they had to end up with the same number of towers that they started with, I still found myself answering that question over and over and over.

It was interesting to watch students try to convince their partners that they had a superior strategy as I circulated.

A few minutes into the activity, I saw students changing up their strategy.  At the beginning of the problems, the students were marking out boxes and moving them one at a time.  This worked, but students soon found it tedious.  Instead, the students started counting all of the boxes in all of the towers.

I stopped by a group just after they reached the conclusion that there were 28 blocks in the towers.  With a perplexed look on my face, I asked them why that information was useful.  The group informed me that because they knew how many towers they needed to end up with that they could take the number of blocks and just divide by the number of towers.

I do have to admit that not all of my groups made this realization.  Some were plenty happy to keep using the same method that worked over and over and over.

When my students got to question 6, they began to become confused.  Really confused.

My students who were rearranging the blocks one at a time found themselves left with 4 extra blocks and 8 towers.  How does that work?

Some groups decided to cut the four blocks in half and distribute one half block to each tower.  The groups that were adding up the blocks and dividing by the towers seemed to have less trouble with this problem.  Many groups, however, got frustrated and gave up when the problem didn’t work out evenly.

After the groups had time to attempt MOST of the problems, I began a class discussion.  I asked the groups to share their strategies.  One student in each class would bring up the fact that they had found a shortcut.  They then proceeded to describe how they had added up all the blocks and divided by the number of towers.

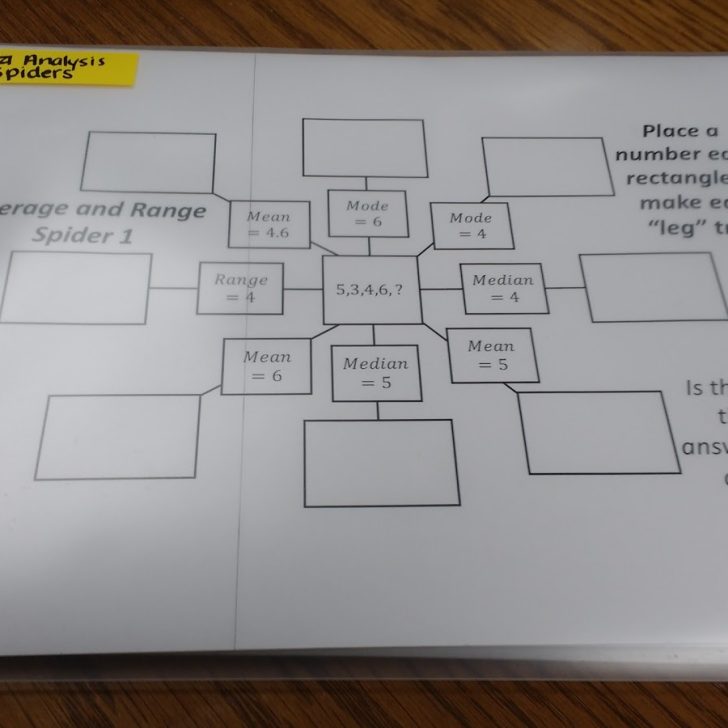
After they finished explaining, I asked them what mathematical concept matched up with what they had just done.  It was so exciting to see their eyes light up as they realized they had just found the mean!

I hope that my students walked away from this lesson with a better understanding of what the mean is instead of just knowing the steps to arrive at the mean.

Thanks Don Steward for this awesome activity!