2024 Challenge: Yearly Number Challenge
This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.
Want to check out my favorite Amazon items for the classroom? Check out my Amazon favorites page!
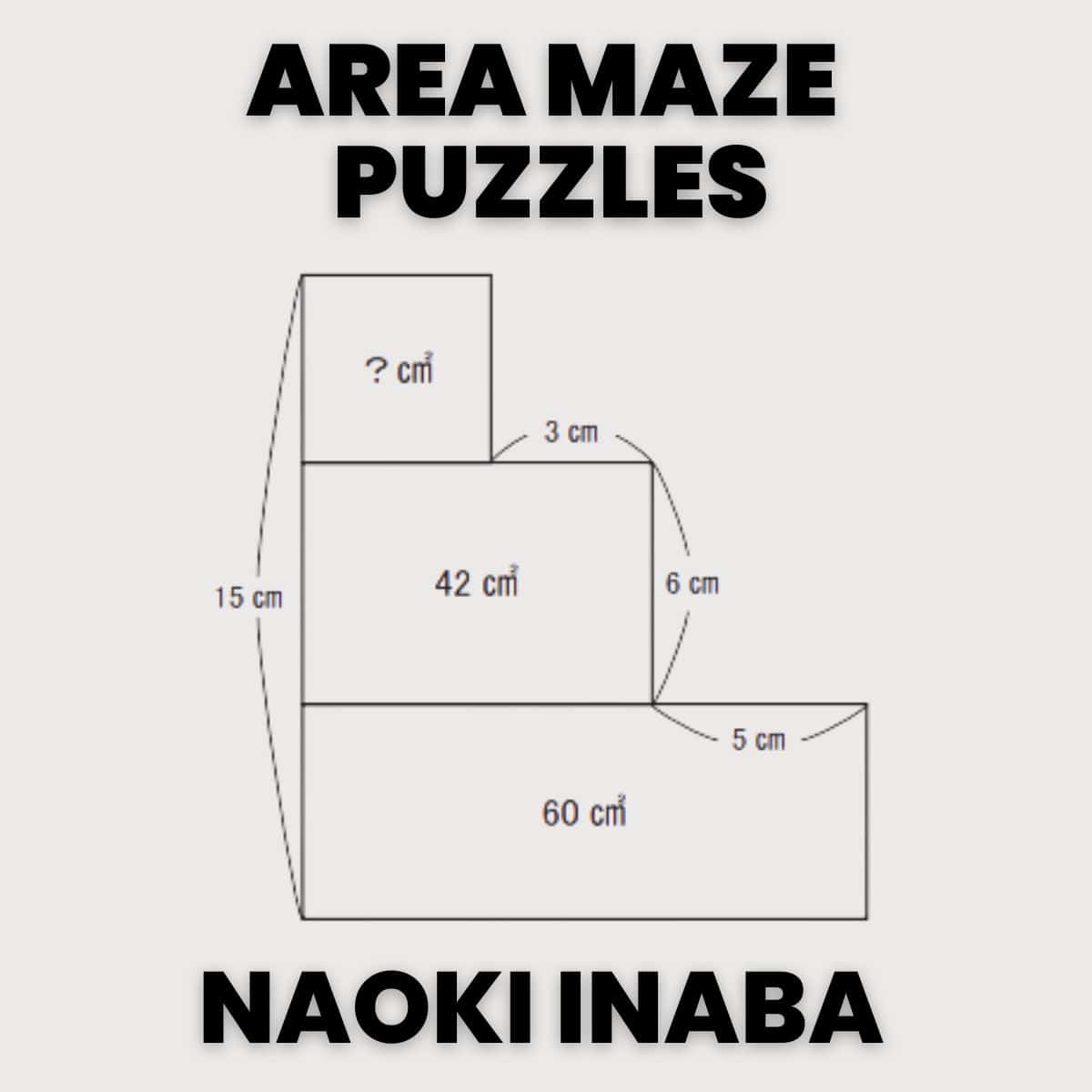
The 2024 math challenge is a simple to explain puzzle that will keep you captivated for hours. Using the digits in the current year exactly one time each, can you write a mathematical expression for each digit between 1 and 100? You may use any mathematical symbol or operation of your choosing.

What is the Yearly Number Challenge?
The 2024 yearly number challenge goes by a variety of different names. You might know it as the 2024 Number Challenge, 2024 Year Game, 2024 Math Challenge, or just the 2024 Challenge.
Whatever you choose to call it, the goal of this math challenge is to use the digits in the current year (2024) exactly one time each along with any mathematical symbol or operation of your choosing to create expressions equivalent to the numbers 1-100.
What Mathematical Symbols or Operations Are Allowed?
Concatenation
- You are allowed to join digits together to form larger numbers. For example, 2 and 0 can be concatenated to form 20. 2 and 4 can be concatenated to form 24 or 42.
Decimal Points
- Decimal points may be placed between digits such as 2.0 or 2.2.
Basic Arithmetic Operations
- Addition
- Subtraction
- Multiplication
- Division
Grouping Symbols
- Parentheses
- Brackets
- Braces
Exponents/Radicals
- If you choose to use an exponent, it must be one of the digits in the year. Additionally, it counts as your use of that digit. For example, in the 2024 challenge, you could use 4^2 + 20 for 36.
- Square roots are allowed. This does not count as the use of the digit 2.
Other Math Symbols
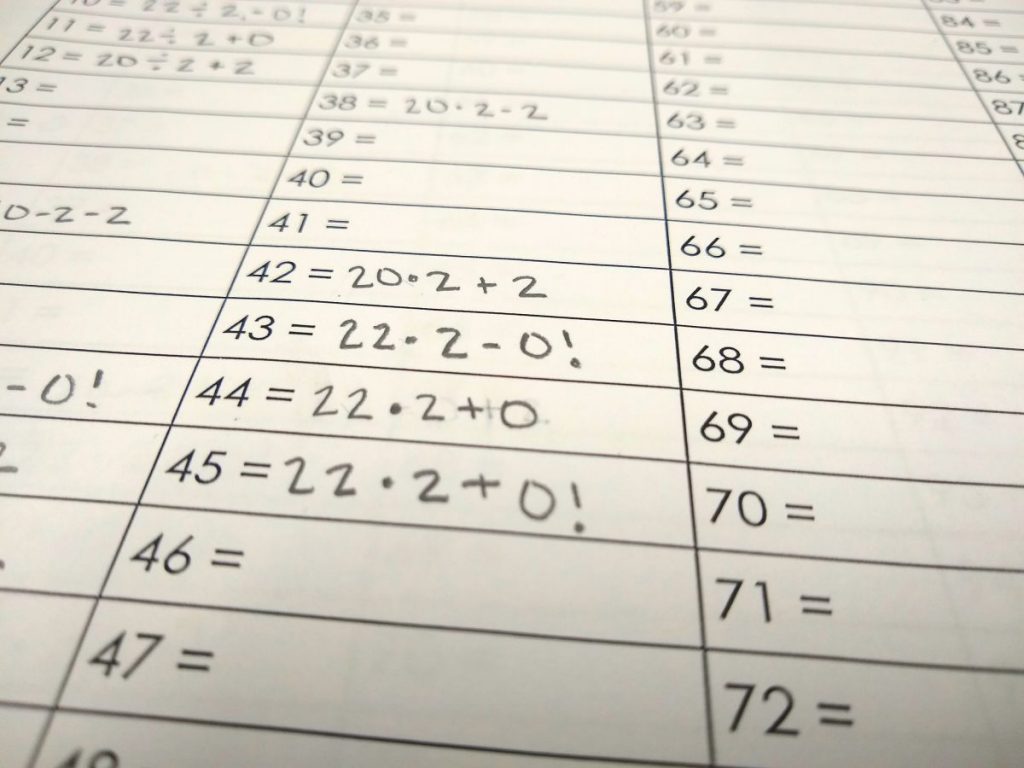
- Factorials – I like to use this activity as a way to introduce my students to the concept of factorials. The factorial of a number is the product of all positive integers less than or to the number.
- 0! = 1 [THIS FACT COMES IN VERY HANDY WITH THIS CHALLENGE!]
- 1! = 1
- 2! = 2 * 1 = 2
- 3! = 3 * 2 * 1 = 6
- 4! = 4 * 3 * 2 * 1 = 24
- 5! = 5 * 4 * 3 * 2 * 1 = 120
- Double Factorials – Double factorials are related to factorials, but they involve multiplying by only the numbers that have the same parity (even or odd) as the original number. [NOTE: Desmos does not evaluate double factorials. It simply applies the factorial function twice.]
- 4!! = 4 * 2 = 8
- 5!! = 5 * 3 * 1 = 15
- 6!! = 6 * 4 * 2 = 48
- In need of a review of how factorials work? I created a free printable factorials table that both reviews the concepts of factorial and double factorial and provides a handy chart of factorial values to reference.
- I also created a free printable factorials poster that you can print and hang in your classroom for students to reference.
- I have seen some people use the floor and ceiling functions in this challenge, but I have never allowed my students or myself to do this. It has always seemed too much like “cheating” to me.

Ultimately, remember that this challenge can be whatever you need it to be. Feel free to change the rules to meet your students’ needs!
Extra Challenge
Want even more of a challenge? How many numbers can you find if you keep the digits in order each time?
NCTM calls this the “Year Game” and encourages students to keep the digits in the original order whenever possible. I often find the challenge is difficult enough without encouraging this restriction.
How Can I Use this Challenge in my Classroom?
I have been using the yearly number challenge in my classroom in various forms since 2016. I originally learned about this task from Jeremy Denton who learned of the challenge from Mr. Collins. I did take a few years off from the activity in 2020 and 2021 due to COVID restrictions and not being able to come up with as many solutions due to the numbers in the year being so small!
Over the years, the challenge has taken various forms. In 2019, I turned the yearly number challenge into a group competition.
For several years (2016-2018), I formatted the yearly number challenge as a free printable bulletin board. Most recently, I have been making a printable challenge sheet with spaces for students to write in each solution as it is found.
WARNING
Some year’s challenges are easier to solve than others. Make sure students realize that they may not be able to find all of the solutions!
2024 Challenge
When I use the yearly number challenge with my high school math students, I challenge them to find mathematical expressions for as many of the numbers between 1 and 100 as possible. I have created a free printable sheet for them to fill out as they find solutions for various numbers.
Some years it is possible to find more numbers in the challenge than other years.

Depending on the age and math ability of your students as well as the amount of class time you would like to dedicate to this activity, you may wish to only have your students find a subset of the numbers.

For the past couple of years, I have ended up creating 6 different versions of the yearly number challenge that you can print and use with your students. Challenge your students to find the numbers 1-10, 1-20, 1-30, 1-40, 1-50, or 1-100 using the digits in 2024.

I would suggest printing off the challenge sheet with all 100 numbers on it and then try to find as many solutions as possible using the type of mathematical operations that you expect your students to use while solving. Once you see how many you are able to solve on your own, you can then decide which level of challenge will be appropriate to your students.
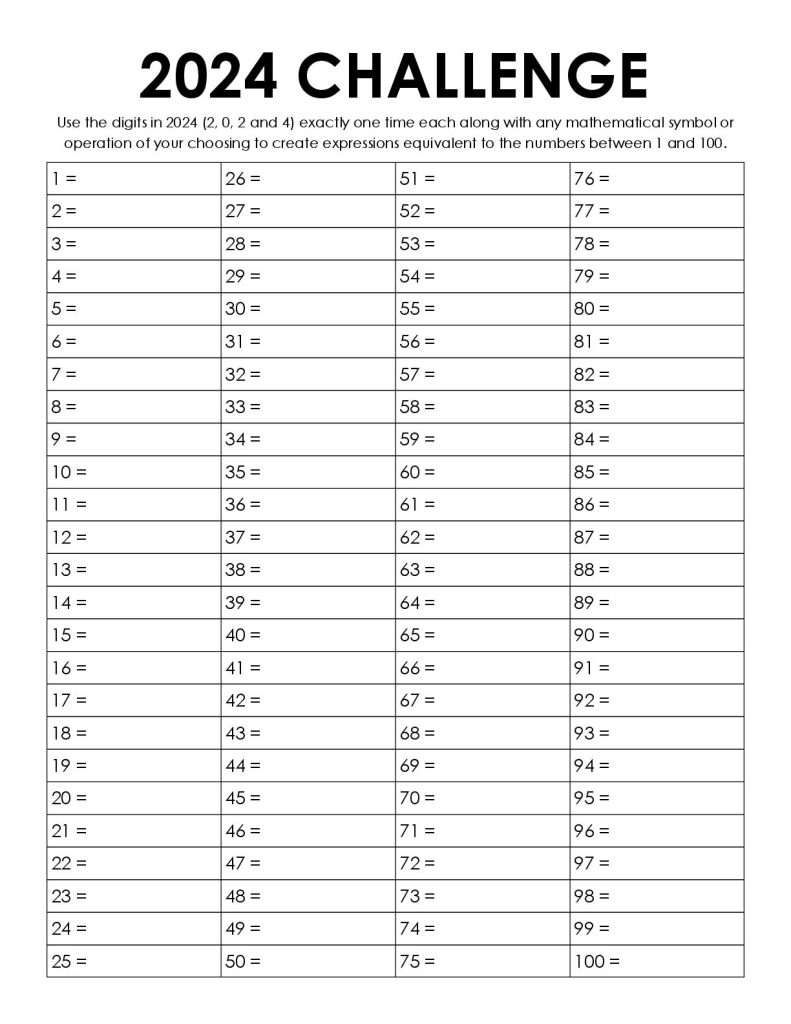





Free Download of 2024 Math Challenge
The 2024 version of the yearly number challenge is available to download as a PDF file and an editable Publisher file. In order to edit the Publisher file, you will need to ensure you have Microsoft Publisher installed on your computer.
2024 Yearly Number Challenge (PDF) (4779 downloads )
2024 Yearly Number Challenge (Editable Publisher File ZIP) (1300 downloads )
I also highly recommend checking out my free printable 2024 puzzle that involves reassembling the digits in 2024 using horizontal and vertical strips of paper. It’s trickier than it looks at first! Over 5000 teachers used the 2023 version of the puzzle in their classrooms, so I can’t want to see what everyone does with the 2024 puzzle.

2024 Math Challenge Answer Key
I am currently crowdsourcing an answer key for the 2024 Number Challenge. If you are a teacher looking for the 2024 Challenge answers or would like to add the answers your class has found to the answer key, send me an email at sarah@mathequalslove.net. I look forward to hearing from you!
Be sure to include information on what/where you teach so I can be sure that you are a teacher and not a student searching for answers!
Puzzle Solutions
I intentionally do not make answers to the printable math puzzles I share on my blog available online because I strive to provide learning experiences for my students that are non-google-able. I would like other teachers to be able to use these puzzles in their classrooms as well without the solutions being easily found on the Internet.
However, I do recognize that us teachers are busy people and sometimes need to quickly reference an answer key to see if a student has solved a puzzle correctly or to see if they have interpreted the instructions properly.
If you are a teacher who is using these puzzles in your classroom, please send me an email at sarah@mathequalslove.net with information about what you teach and where you teach. I will be happy to forward an answer key to you.
Additional Resources and Ideas
Introducing Students to Factorials
I published some information on how I introduce students to the concept of factorials in 2022 when I blogged about the 2022 Challenge.
I actually kicked off class with an ACT question featuring factorials. The majority of my students have never encountered factorials before, and I knew that we would have much more success with the challenge if we were able to capitalize on the fact that 0! = 1.
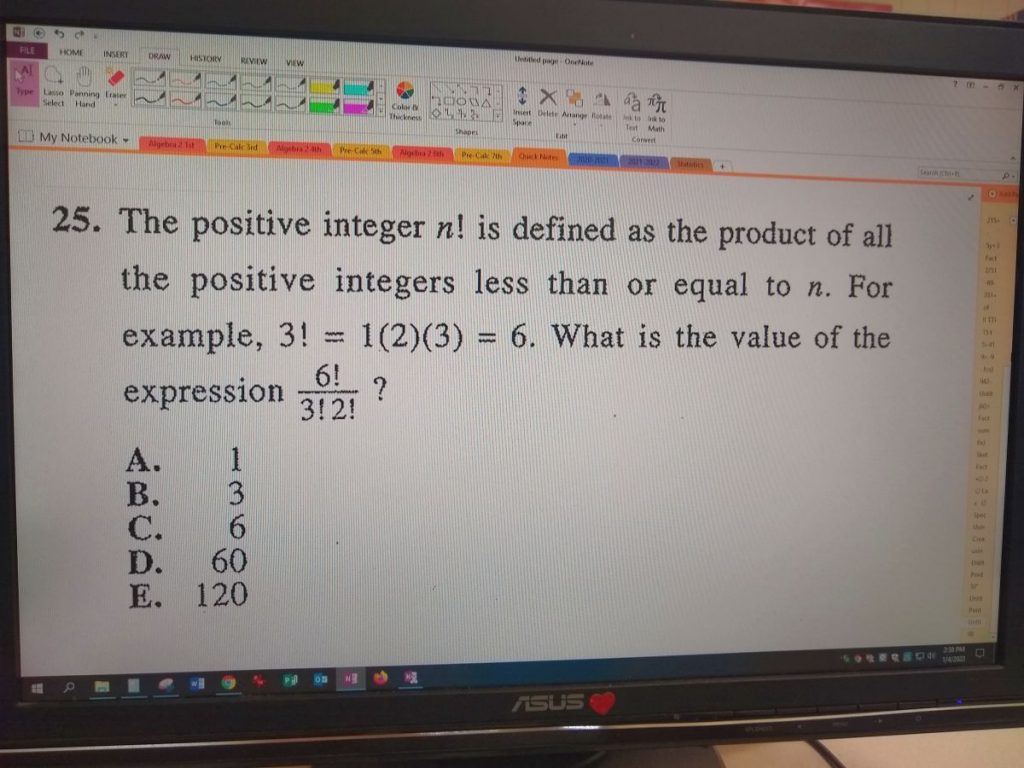
We worked through the ACT problem, I taught them the word “factorial,” and then I challenged them to use their new understanding of factorials to determine the value of 0!.
After revealing that 0! is 1, I told them that this fact might come in handy today and handed out the 2022 Challenge worksheet.
In 2019, I took a slightly different approach to introducing the concept of factorials. We started by trying to complete this chart.

We started by trying to complete this chart as a class on the dry erase board. It was interesting to hear students’ theories evolve as each new answer was revealed.

Ideas for Motivating Students to Complete the Challenge
Bulletin Board Puzzle for Early Finishers
The first few years I ran this yearly challenge (2016-2018), I posted it as a bulletin board in my classroom for early finishers to work on throughout the month of January. Or to be honest – until I got around to changing the bulletin board!
It always brought great joy to me to see groups of students clustered around the bulletin board (or dry erase board) while discussing that year’s number challenge.

I designed the bulletin board version of this puzzle to be printed on 11 x 17 cardstock.

The 11 x 17 poster templates have spaces to write a solution and the name of the person that came up with the solution next to each number. Even though I haven’t updated the bulletin board versions in several years, you can easily download an older year’s template and update the instructions to use the current year’s digits. Everything else can stay the same.
I decided to add visual reminders of which operations are allowed to spice up my bulletin board a bit.

I made space on one of the posters to include the instructions to the puzzle. This meant that students could get started solving the puzzle without any guidance from yours truly.
Though, I usually make it a rule that ALL solutions must be verified by me before being added to the posters!

You and your students will love watching the bulletin board fill up with solutions. I found that as the bulletin board started to fill up, more and more students became invested in the puzzle and wanted to join in and help.
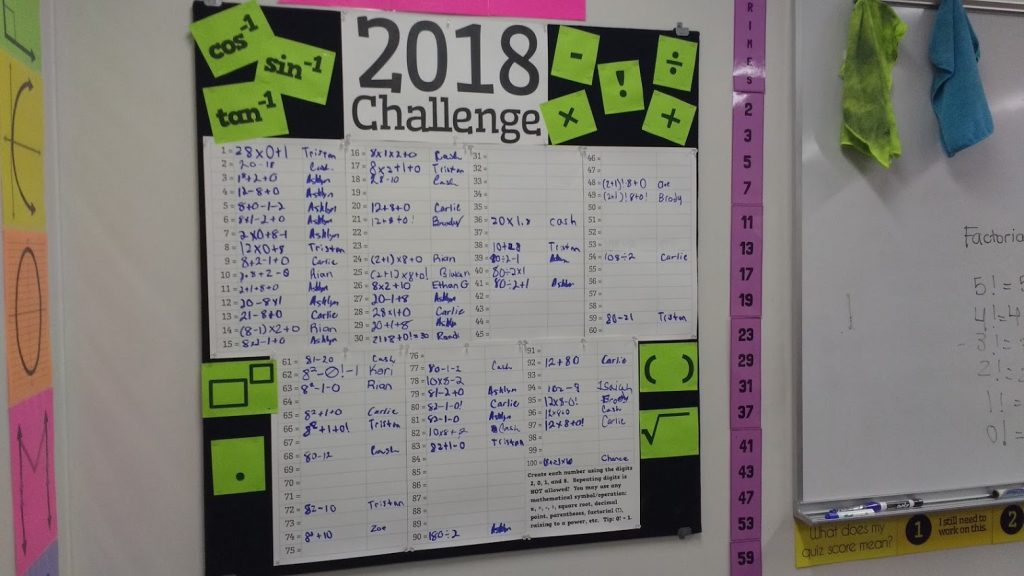
The bulletin board files I have made over the years are available to download at the bottom of this blog post. You will need to update the year to match the current calendar year.
Class Period Competition
One year, to give my students a bit of extra motivation to engage with the activity on the first day back from break, I decided to pit my classes against one another in a contest. I told them whichever class period found the most solutions to the challenge would win cookies.
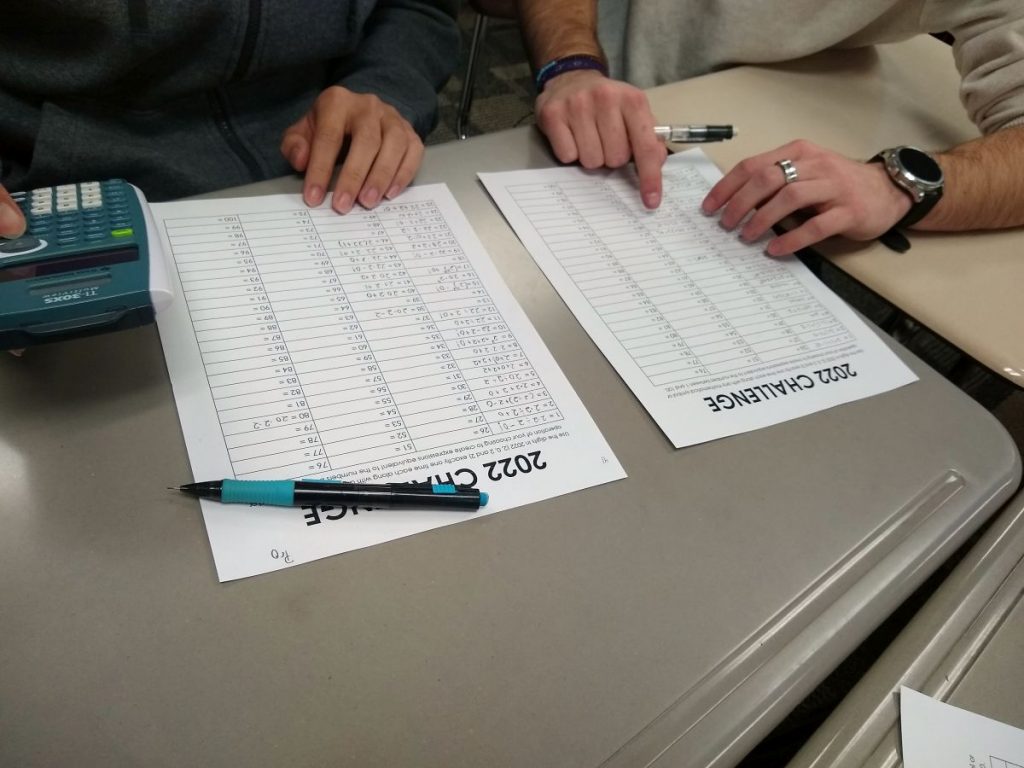
Apparently, teenagers love food because I found that my students were engaged and quite competitive. My afternoon class even went as far as to compile all of their results on the dry erase board to make sure that students weren’t working on numbers that had already been solved by another group.
They also argued that their class was at a disadvantage since they had half as many students as some of my other classes. They wanted me to change the rules to make it ratio based, instead.
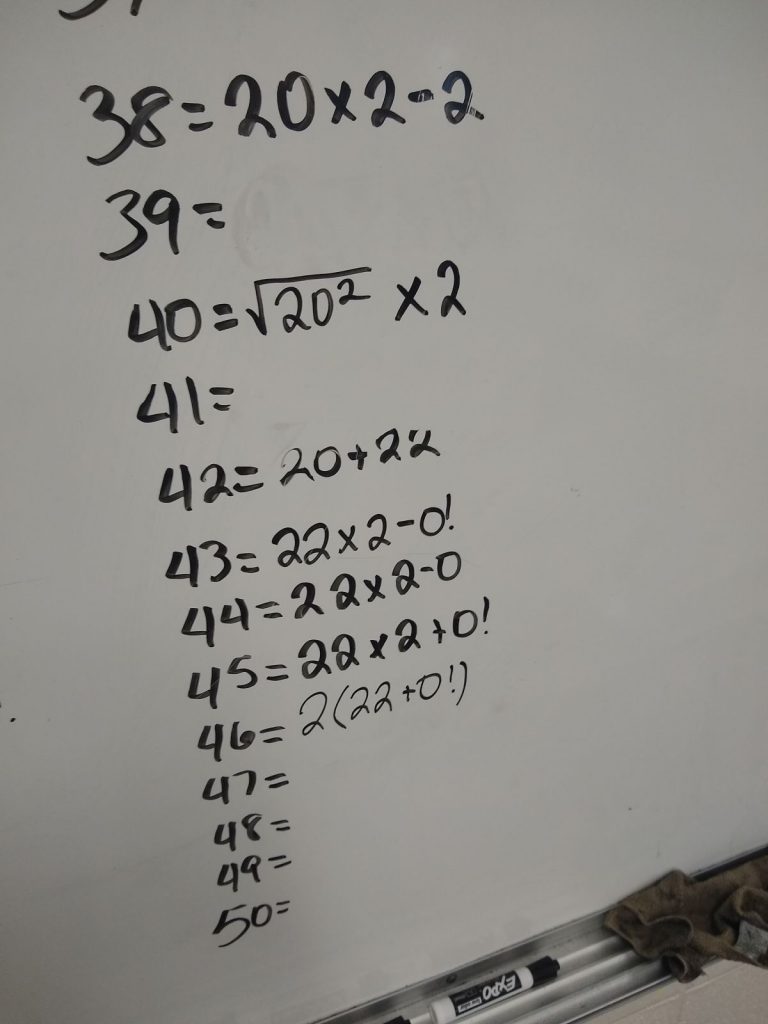
Group Competition
Back in 2019, I decided to take the yearly number challenge which I had previously just used with early finishers and turn it into an entire class activity where different groups of students were competing against one another.

I walked the entire class through a slide presentation to introduce the activity.
I gave them a list of some of the possible mathematical operators to get their brains moving.

In the past, I would post the challenge, introduce it to my students, and let them fill out as many solutions as possible. As the first day would progress, the challenge would get more and more difficult as the easier numbers that could be achieved by simple addition and subtraction with maybe a little multiplication thrown in were already claimed.
I needed to keep six entire classes of students engaged, so I decided to have each class start the challenge from the beginning. That’s when I got the idea to pull out my 100 number chart that I purchased last year from Amazon.

Then, I spent some quality time with the paper chopper and some cardstock to cut out a different colored set of squares for each of the six groups that my desks are arranged in. I sized these squares to be the same size as the 1-100 cards that fit in my 100 number chart.

Groups would work together to find as many expressions as possible to equal numbers between 1 and 100. When a group found an expression for an unclaimed number, they would bring their solution up to get it verified.
If it was correct, they would place one of their squares of cardstock on top of the number to “claim” it for their team.

By the end of the 50 minute period, the board would look something like this:

In some ways, this activity structure was better than my bulletin boards of the past. And, it also left some attributes to be desired. Let me try to reflect.
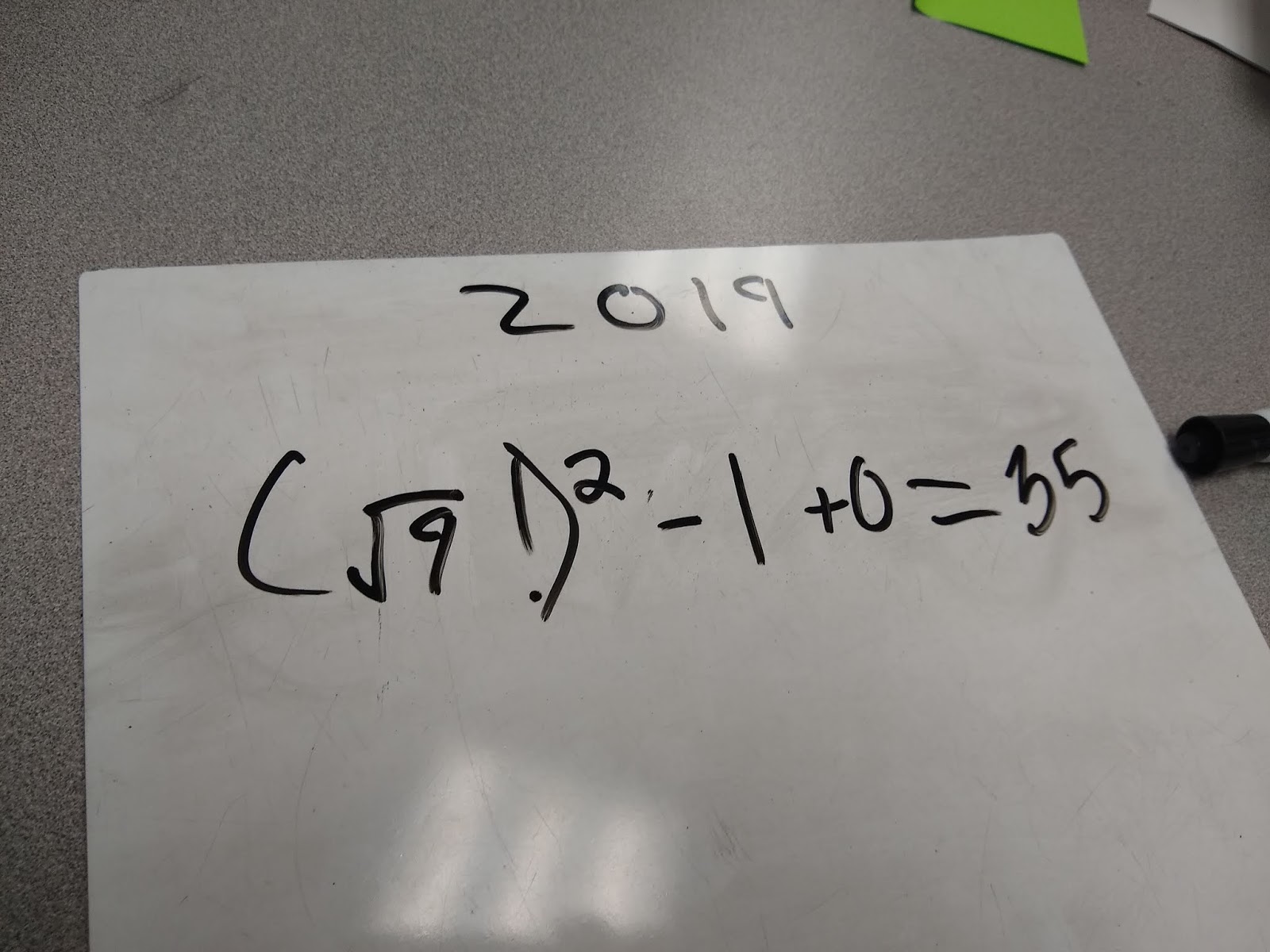
Adjusting this to a group-based competition did have some unintended consequences.
Some groups were WAY more hyper-competitive than I expected.
One group had one of their team members permanently stand next to the 100 number chart so that as soon as they figured out a number and got their solution checked they could mark it with the color for their team. This meant that this student was not doing any math at all which was not my intention.
I attempted to combat this by requiring in another class period that only one person from each group was allowed out of their seat. This solved the prior issue but created another.
One student from the group would tend to spend the entire time running answers up to my desk and getting them checked before marking off their numbers on the chart. This meant that there was still a student who was primarily doing no math at all.
Still yet another downside to the competitive team nature of this activity was that some groups tended to give up entirely as they realized JUST how far they were behind the other teams.
Some students started trying to play games on their phones instead of participating in the activity because they knew that their group was NOT going to win.
To combat this in the future, I might have students remove the cards from the chart after solving them and have them place them in a small box or basket for each team.
This way, everyone can still see what numbers remain unsolved, but they can’t easily see how far ahead or behind they are from the other teams.
I really appreciated the fact that making this into a group activity ended up engaging a vastly larger percentage of my students than my previous use of the activity with early finishers.
However, a trade-off was that my students weren’t necessarily learning from one another as much as they have in the past. This was because previously, students would write their solutions to each number on the bulletin board.
Often, students would take a solution for one number and end up tweaking it slightly to create a different number. Usually, this would involve adding a factorial symbol to a 0 to produce a 1 or something similar to that.
Frequently, students would see a solution written on the board and ask a question about it, thinking it was incorrect. This made a great teaching moment.
If I do this again, I might write 1-100 on the dry erase board and have students write their solutions next to each number as a step in the process. This keeps the competitive aspect while still encouraging students to learn from one another. It’s also easily erasable between classes.
Previous Year’s Challenges
Looking for printable versions of previous year’s challenges? I have kept the previous versions available below.
2023 Challenge Worksheet
The 2023 Challenge was also available as a digital challenge via Desmos Activity builder thanks to Craig Winske.
2017 Challenge Bulletin Board

2017 Challenge (PDF) (1548 downloads )
2017 Challenge (Editable Publisher File ZIP) (1535 downloads )
For the Publisher file, you’ll need this free font: Wellfleet
2016 Challenge Bulletin Board

2016 Challenge (PDF) (1645 downloads )
2016 Challenge (Editable Publisher File ZIP) (1509 downloads )
For the Publisher file, you’ll need this free font: HVD Comic Serif Pro.