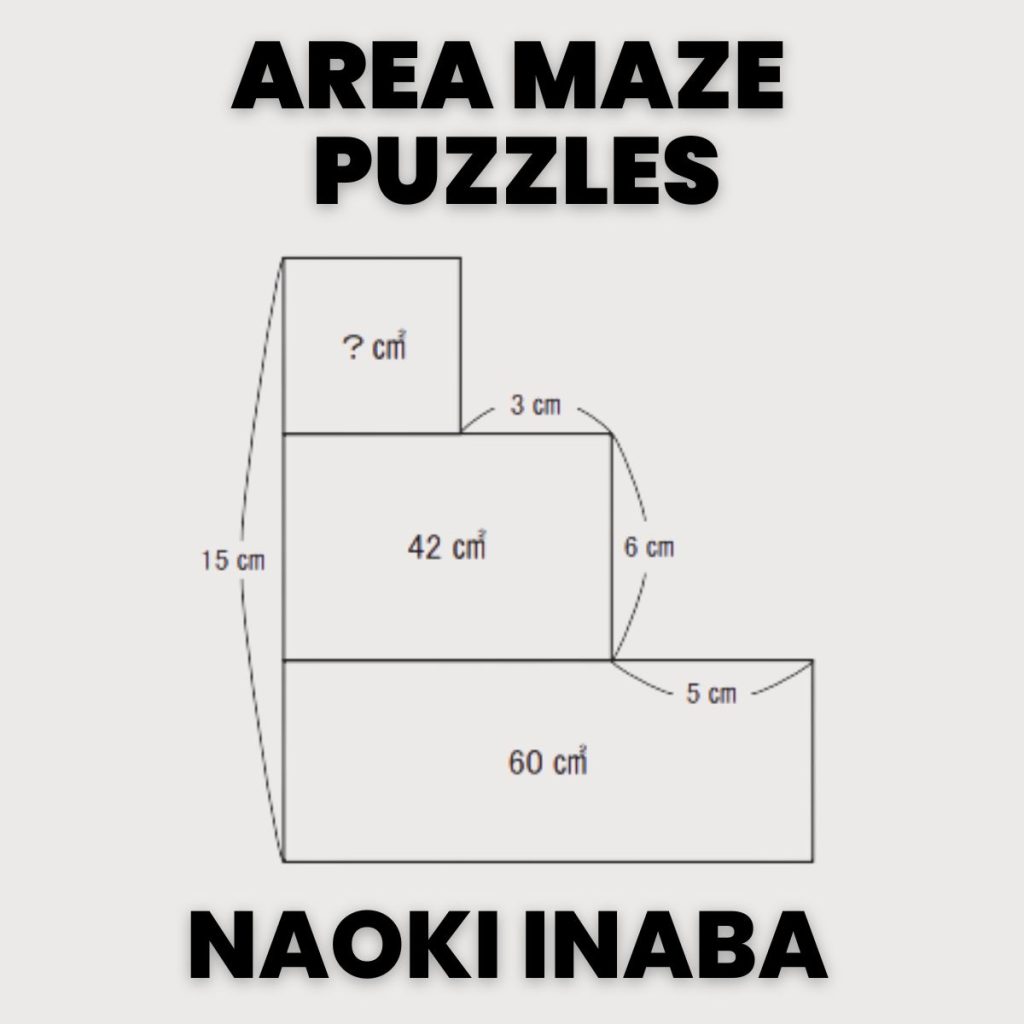
Area Maze Puzzles
This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.
Area Maze Puzzles from prolific Japanese puzzle creator Naoki Inaba have become quite popular in the United States. This hasn’t always been the case.
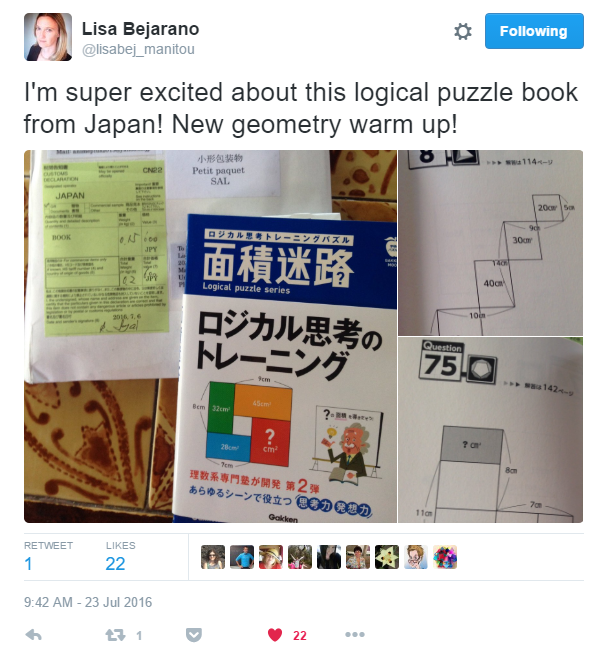
I first learned about these puzzles from a tweet from Lisa Bejarano. At the time of her tweet, you could only really get your hands on a large number of area maze puzzles by ordering them from Japan.
Area Maze puzzles, also known as menseki meiro puzzles, are an original creation of Naoki Inaba. Inaba is a Japanese puzzle author who has created over 400 different types of puzzles.
If you’re a die-hard logic puzzle lover, I highly recommend purchasing a copy of Inaba’s book: The Original Area Mazes.

He has since followed this up with both a second volume of area maze puzzles and a volume geared toward kids.
So, what is an area maze puzzle?
I really like the example puzzles provided in this article from The Guardian by Alex Bellos. In fact, Alex Bellos actually wrote the introduction to Inaba’s The Original Area Mazes book.
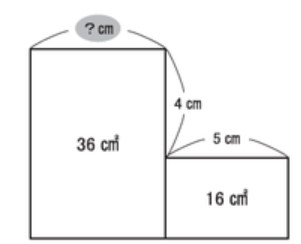
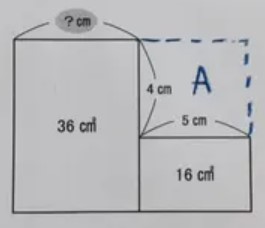
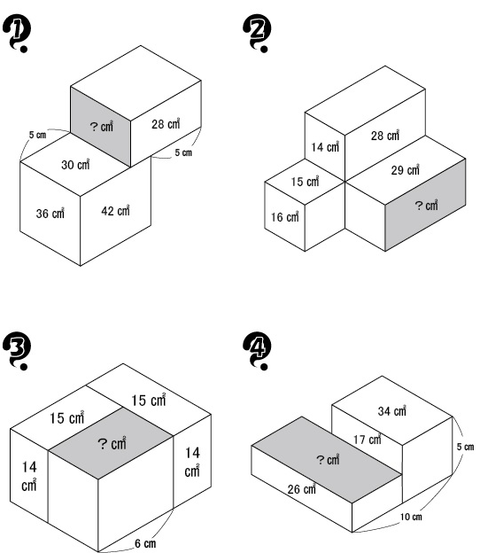
The goal of the puzzle is quite simple: figure out the value of the question mark. One caveat: you are NOT allowed to use fractions in your solution. All of these puzzles can be solved using ONLY whole numbers.
To solve the puzzle above, you’re going to need to think outside of the boxes provided. Alex Bellos offers up this hint in his Guardian article. If we form another rectangle as shown below, we can easily find its area. After all, we know its length and width. We can also realize that the rectangle on the left and the two rectangles on the right both have the same area. If they have the same area and the same height, they must also have the same width. Isn’t that an incredibly satisfying feeling?
Want more puzzles to solve? I know I do! Here are some sources of free area maze puzzles to keep you busy while you wait on a copy of Inaba’s full book of puzzles to arrive at your doorstep.
Sources of Free Area Maze Puzzles (Menseki Meiro Puzzles)
The article in The Guardian by Alex Bellos that I referenced above has a total of 5 puzzles embedded in the article.
There is also a blog post from the New York Times that features the puzzle. This blog post links to two pdfs of puzzles that you can download here and here. And, for the record, these puzzles get quite large and complex. Don’t believe me? Just click on that last link! The bottom of the New York Times Post also includes a 3D Version!
Naoki Inaba, the creator of the Area Maze puzzles, has also posted four free puzzles as a PDF on his website. The text is in Japanese, but this won’t keep you from working the puzzles.
The Waterloo Region District School Board has a page of puzzles and riddles for elementary students to tackle. They feature several area maze puzzles as well as questions and prompts to use with students as they are tackling these puzzles.
Five Thirty Eight features two of Inaba’s area maze puzzles on their website for you to try your hand at.
If you have a free account on TES, there is a free printable of area maze puzzles to use with your students.
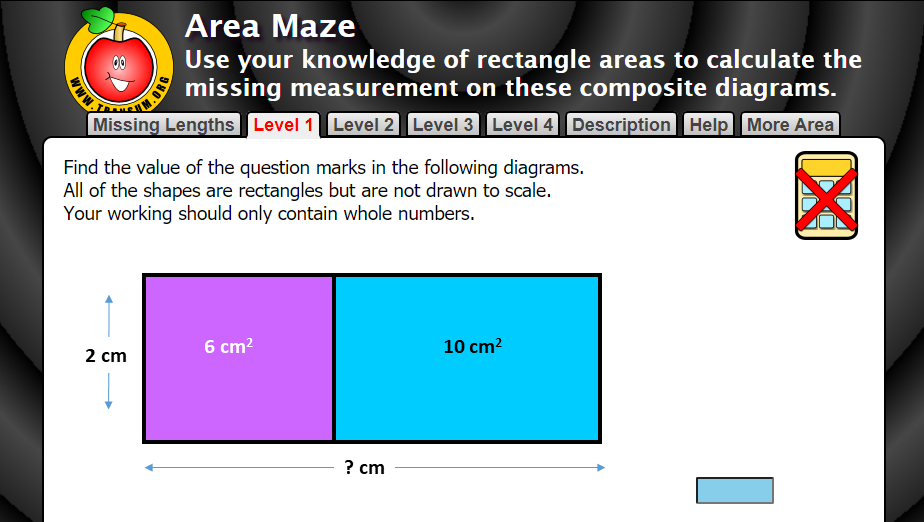
Transum (an all around lovely site for math teachers with tons of free resources) has four levels of area maze puzzles for students to work through. They are even self-checking!
Rose Lorenz has put some of the area maze puzzles into Desmos Activity Builder to make them easier to use with students.
I think these would make good warm-up puzzles in the classroom. They’d also be great to stick in a unit on area or volume! Or, you could use them as a sort of brain break. Stick one of these in your slides to give your students a quick challenge and break from whatever topic you are working on.
Looking for more amazing logic puzzles from Naoki Inaba to use in your classroom or to solve yourself? Check out these other puzzle posts:
Interested in just more puzzles in general? I’ve got a whole page on my blog dedicated to all things puzzles.
Puzzle Solutions
Puzzle solutions are available on a password-protected solution page. I do not openly post the puzzle answer keys because one of my goals as a resource creator is to craft learning experiences for students that are non-google-able. I want teachers to be able to use these puzzles in their classrooms without the solutions being found easily on the Internet.
Please email me at sarah@mathequalslove.net for the password to the answer key database featuring all of my printable puzzles and math worksheets. I frequently have students emailing me for the answer key, so please specify in your email what school you teach at and what subjects you teach. If you do not provide these details, I will not be able to send you the password.
Not a teacher? Go ahead and send me an email as well. Just let me know what you are using the puzzles for. I am continually in awe of how many people are using these puzzles with scouting groups, with senior adults battling dementia, or as fun activities in their workplace. Just give me enough details so I know you are not a student looking for answers to the puzzle that was assigned as their homework!






I was also excited and did a little bit of research after seeing Lisa's post. I have tried out the Android app and it's a little clunky, but there are lots of available puzzles. I am planning to use them as warm-ups. (Maze Monday?)
I like it!
I just spent an hour on the iPhone app solving these puzzles. I am completely hooked. The puzzles focus on logic, proportional relationships and most of all number sense. I definitely see them having a place in my classroom.
I downloaded the app and spent some significant time on it, too!
I think I'm going to use this as a first day of school activity for Geometry. I think I'll also bring them back as we start to do 2-column proofs to remind them about perseverance, and how we might have to alter our thinking to reach the end goal of proving something.
Please blog about how it goes!
I'm totally going to start using these at the beginning of the PD I deliver to my math teachers! It'll be a great warm up and something for them to do while we're waiting for the stragglers.
Great idea!
I bought the book after seeing Lisa's post-and I loved reading your posts on it! Thanks for the links to the previews-it's so cool that the language doesn't matter in math. I also love Sarah Millard Lanahan's idea for PD!! I teach adults at night and can't wait to use these with them as well as my middle schoolers. Keep blogging-I love what you're doing!!! @debboden
Thanks Debbie!
Using these today! So excited – keep forgetting about them and then keep resdicovering them through endless reading of your blog – which is one of my favourite things! Thanks for these 🙂
"Thanks debbie"