Zukei puzzles are the brilliant creation of Naoki Inaba. Inaba has posted these puzzles for free on his website, but it can be a bit hard to navigate since everything is written in Japanese.
You may have heard of Inaba from his popular area maze puzzles.
Instructions for Solving Zukei Puzzles
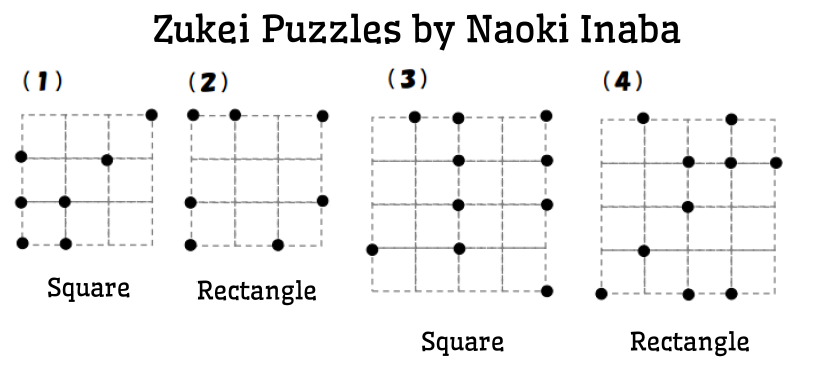
The instructions for the puzzles on Inaba’s website are probably crystal clear if you can read Japanese. Inaba’s original file features 42 puzzles. I used google translate to translate the clues for each puzzle. I made this google doc as a key to allow the puzzles to be used in an English speaking classroom.
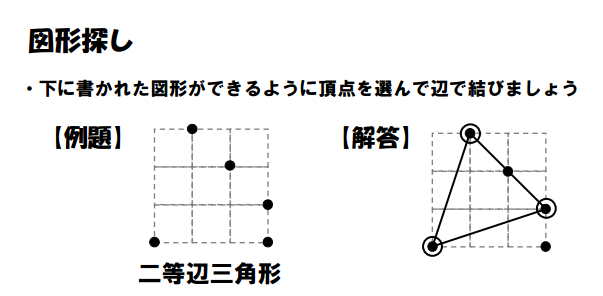
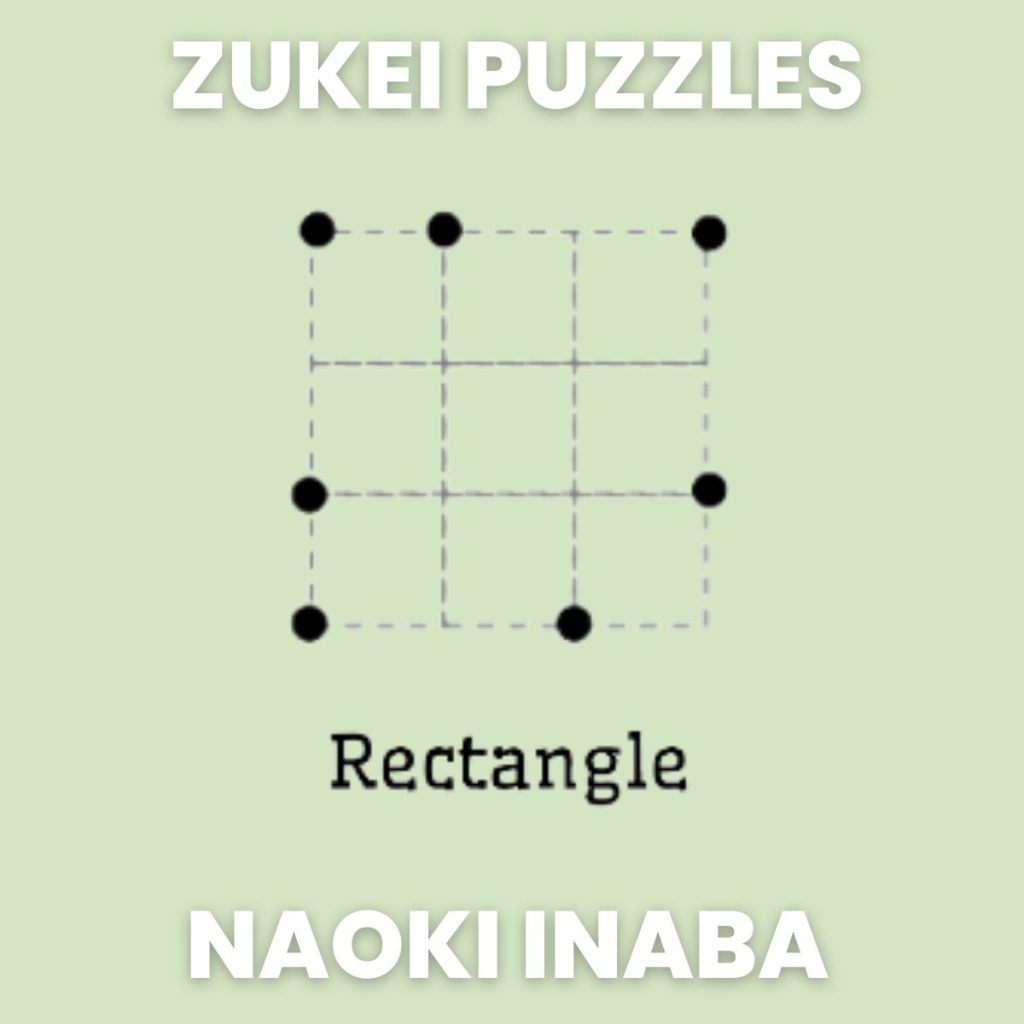
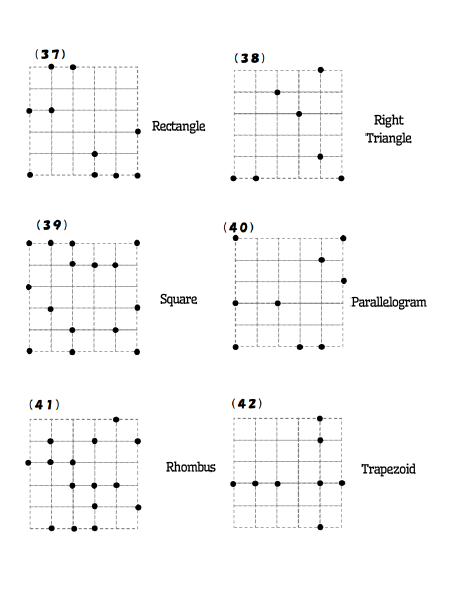
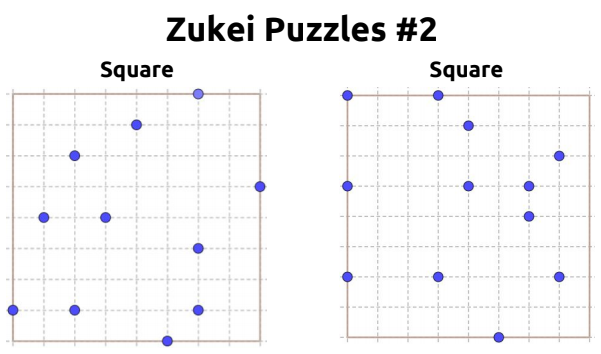
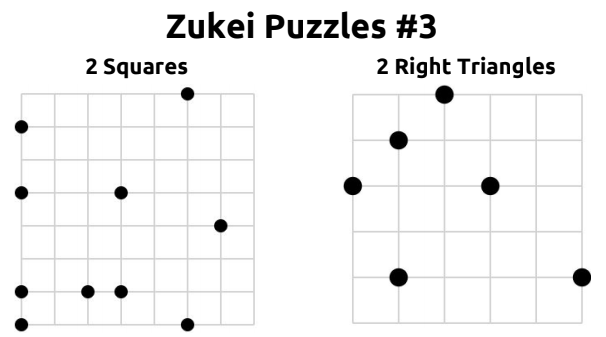
Each zukei puzzle provides you with a grid featuring several dots and the name of a shape. The task is to connect some of the provided dots to form the specified shape. The dots must lie on the shape’s vertices.
This puzzle is perfect for practicing geometric vocabulary. These puzzles focus on 8 different shapes:
- Square
- Rectangle
- Isosceles Triangle
- Isosceles Right Triangle
- Right Triangle
- Rhombus
- Trapezoid
- Parallelogram
I have used these puzzles with high school students. They are generally familiar with all of these shapes, but they often need a reminder of the meaning of the word isosceles. They also tend to confuse trapezoids and parallelograms.
If you want to use these puzzles with younger grades, it would be easy to use the snipping tool to only select the puzzles that match with the vocabulary you are wanting to practice or your students are familiar with.
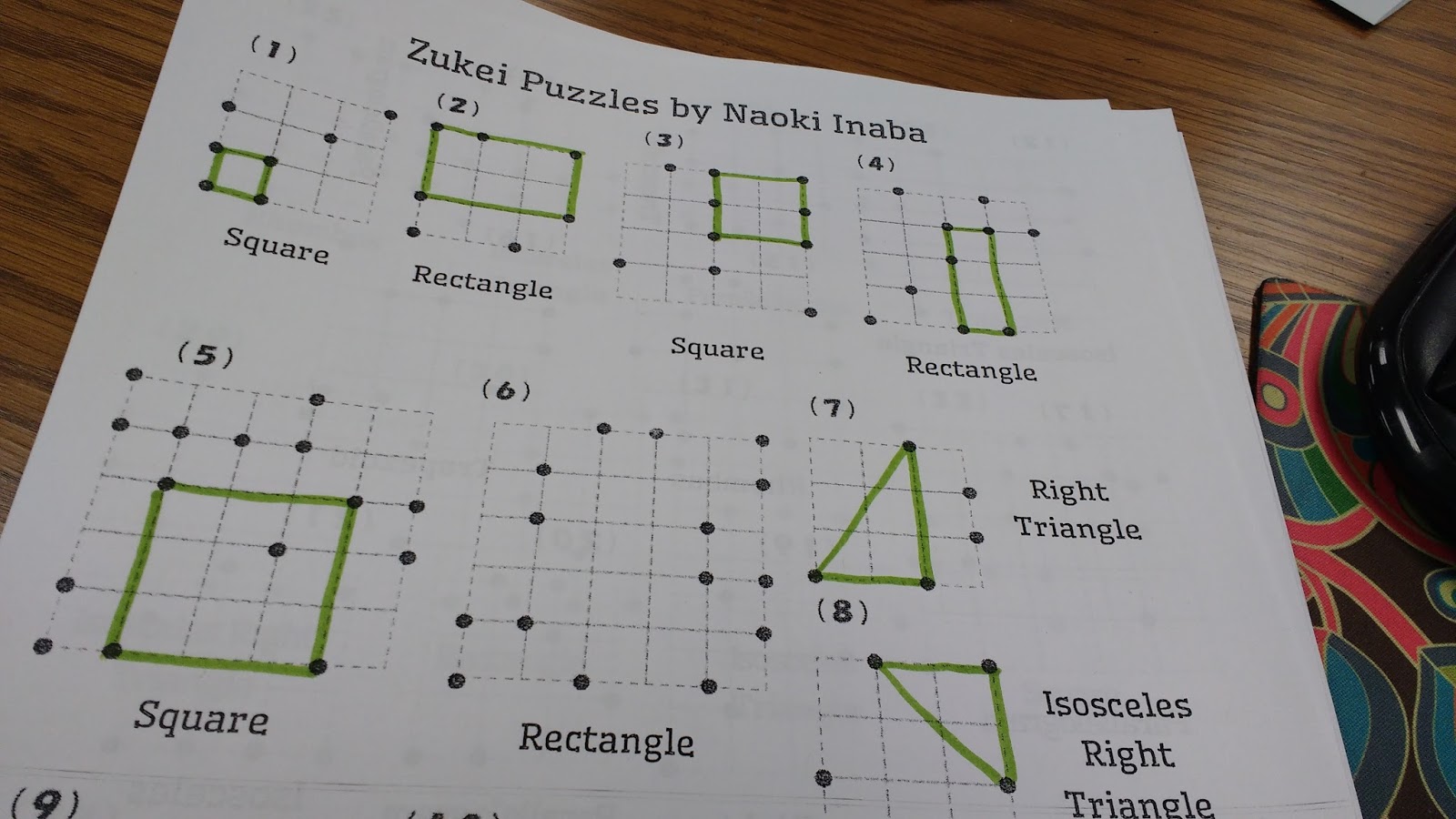
These puzzles are fun. And, they are frustrating! We won’t talk about how long I was stuck trying to figure out puzzle number 6! In fact, I only figured it out because a student spoiled it for me!
Free Download of Zukei Puzzles
Zukei Puzzles by Naoki Inaba (PDF) (5526 downloads )
Zukei Puzzles by Naoki Inaba (Editable Publisher File ZIP) (2195 downloads )
I feel like I need to remind you once again that I did not create these puzzles. I simply re-formatted them to make them usable in English speaking classrooms. All of the puzzles were created by Naoki Inaba.
Puzzle Solutions
I intentionally do not make answers to the printable math puzzles I share on my blog available online because I strive to provide learning experiences for my students that are non-google-able. I would like other teachers to be able to use these puzzles in their classrooms as well without the solutions being easily found on the Internet.
However, I do recognize that us teachers are busy people and sometimes need to quickly reference an answer key to see if a student has solved a puzzle correctly or to see if they have interpreted the instructions properly.
If you are a teacher who is using these puzzles in your classroom, please send me an email at sarah@mathequalslove.net with information about what you teach and where you teach. I will be happy to forward an answer key to you.
Other Sources of Zukei Puzzles and Zukei Resources
More Original Zukei Puzzles from Mark Chubb
Want even more zukei puzzles? Mark Chubb has created three sets of additional zukei puzzles in PDF form. I especially like that the third set has students find multiple shapes on one grid! Each set has twelve additional puzzles.
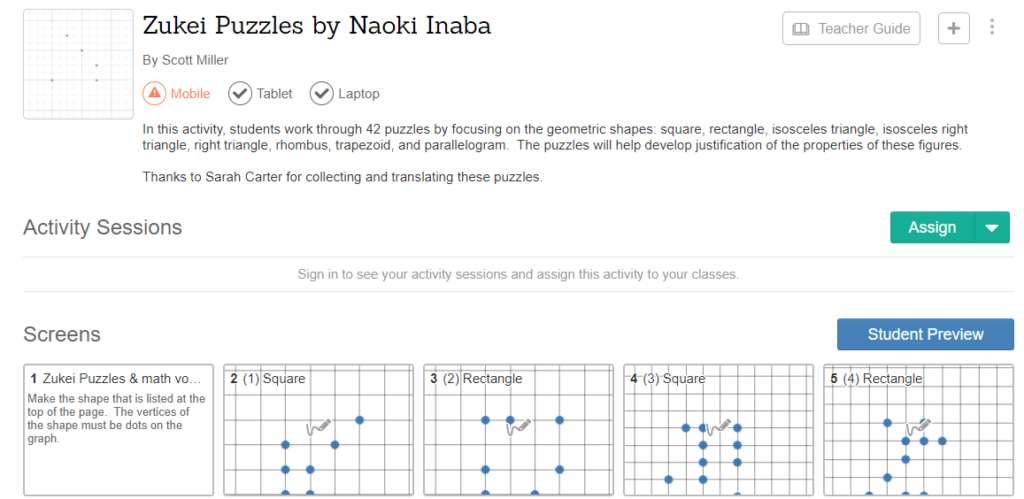
Desmos Activity Builder Version of Zukei Puzzles
Scott Miller has recreated Inaba’s original 42 puzzles in Desmos Activity Builder.
Zukei Puzzle Solver/Puzzle Creator
Shaun Carter has coded a zukei puzzle solver. Build a grid of dots and specify the shape. Your solution will be found instantly.
This would be a great tool if you wanted to create your own puzzles and be sure there was exactly one solution.
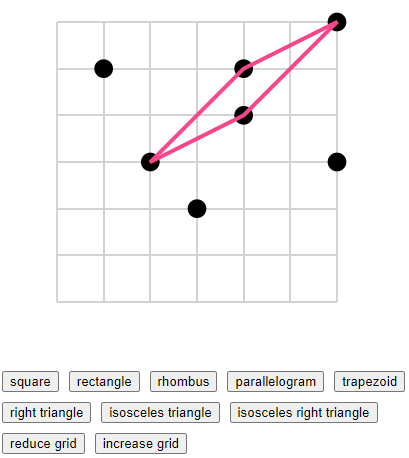
How to Solve Zukei Puzzles Video by Jennifer Chou
Jennifer Chou has filmed a short video about how to solve zukei puzzles. This would be especially great if you are trying to use these puzzles in a distance learning setting.
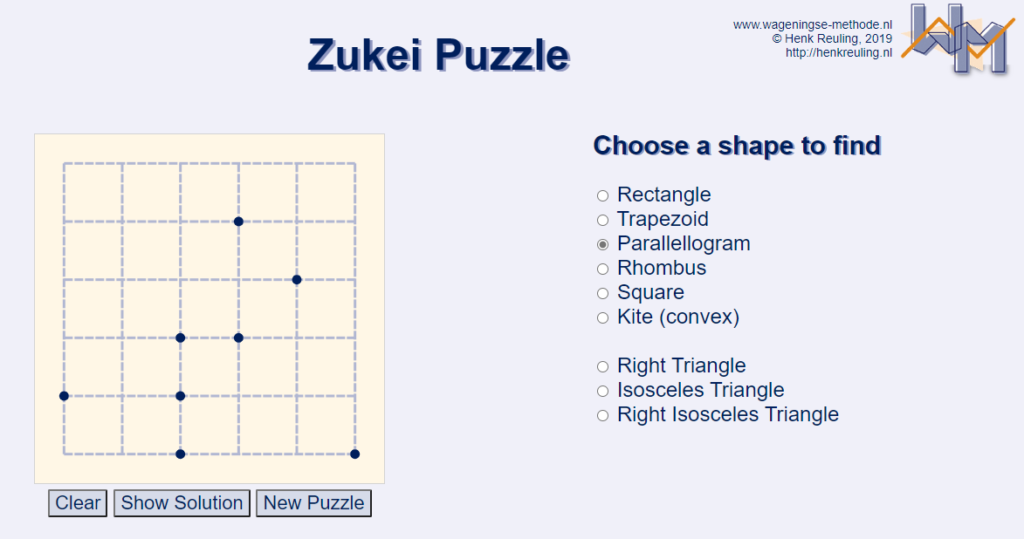
Online Zukei Puzzle Applet from Henk Reuling
Want to play these puzzles online? Henk Reuling, a maths teacher in the Netherlands, has coded a lovely applet for solving an infinite number of puzzles. You even get to choose the type of shape you want to look for!
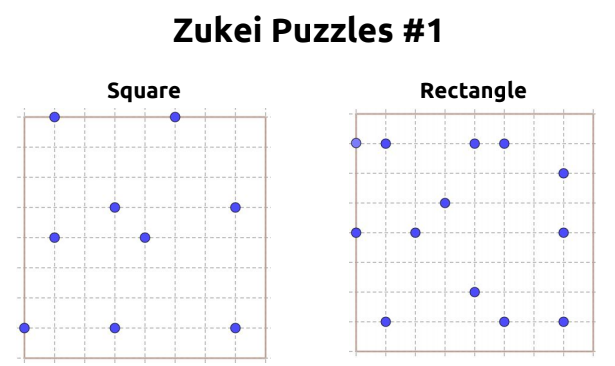
48 Additional Zukei Puzzles from Don Steward
The late Don Steward created 48 additional zukei puzzles which he published under the name “Find the Shape Puzzles.”
Looking for more puzzles? Check out this entire page dedicated to the creative puzzles of Naoki Inaba.
More Printable Paper and Pencil Logic Puzzles
- Sixes Number Challenge
- 3-1-4 Pi Day Number Challenge
- Sankaku Puzzles
- Strimko Puzzles in the Classroom
- Square Sudokus
- Make It Pythagorean Puzzles
- Number Ball Puzzles by Naoki Inaba
- Hidato Puzzles
- Step Puzzles by Naoki Inaba – A Logic Puzzle for Introducing Arithmetic Sequences
- Kazu Sagashi Puzzles from Naoki Inaba
- Factor Tree Puzzles Inspired by Dr. Harold Reiter
- Strimko Logic Puzzles Review
- Tents and Trees Puzzles
- Slants Puzzles
- Angle Mazes by Naoki Inaba
- Zukei Puzzles
- Japanese Logic Puzzles for the Secondary Math Classroom
- Area Maze Puzzles from Naoki Inaba
- Masyu Puzzles
- KenKen In The Classroom
- Futoshiki Puzzles
- Hashi Puzzles
- Shikaku Puzzles
- Nonogram Puzzles
- Digit Cells Puzzle
Anonymous
Tuesday 10th of January 2017
Would you be willing to share the answers?
Sarah Carter (@mathequalslove)
Wednesday 19th of April 2017
Answers are posted on Inaba's website here: http://inabapuzzle.com/study/zukei_a.pdf
Anonymous
Tuesday 10th of January 2017
Google Zukei or Naoki Inaba. You will find the puzzles and solutions.
Unknown
Sunday 8th of January 2017
Please excuse me if this question makes me sound a bit thick, but I'm not totally sure of what the instructions are. Is the user to construct the given polygon using some combination of the dots as vertices? I notice some other folks had the same confusion.
Thanks in advance...
Anonymous
Tuesday 10th of January 2017
Yes, find the given shapes using the dots as vertices.
Anonymous
Thursday 5th of January 2017
Sarah- thanks SOOOO much for the translating and formatting!!!! These are awesome. A word of warning- if your students have instant access to the internet (iPads for all at my school), they will be very tempted to google Naoki Inaba and find all the puzzles and their solutions. Doesn't leave much to the imagination... Even though I am only giving my kids one page at a time, next year I will block out the name of the puzzles and the author before I hand out the first one. That way, they can't google it and spoil the fun. I will put Zukei and Naoki Inaba on the LAST page instead- especially since the last page is the hardest. I want to give him credit, but not give the students the cheaty path to the answers. (My kids are so darn competitive!) -snapdragon
KD
Thursday 5th of January 2017
So much fun for my grade 8 students! Thanks for taking the time to translate and post these. It's much appreciated!
Jenn Hartley
Wednesday 21st of December 2016
#6 also has another solution. If you consider the bottom left corner to be the origin, the rectangle has vertices at (2,0),(1,1),(5,2),(4,3). :-)
Anonymous
Thursday 5th of January 2017
Actually, that's a parallelogram, not a rectangle. Check to see the slopes of the sides- they aren't opposite reciprocals.