Futoshiki Puzzle Collection
Can you place the specified numbers these futoshiki puzzles so that numbers are not repeated in any row and column and all inequality statements are true?
What are Futoshiki Puzzles?
Futoshiki puzzles are a grid-based number puzzle that are a variant of a latin square puzzle. In a latin square puzzle, you must place numbers so that each number appears once in each and every row and column. Futoshiki puzzles build upon this structure by requiring all of the inequality symbols placed between the grid cells to be obeyed.
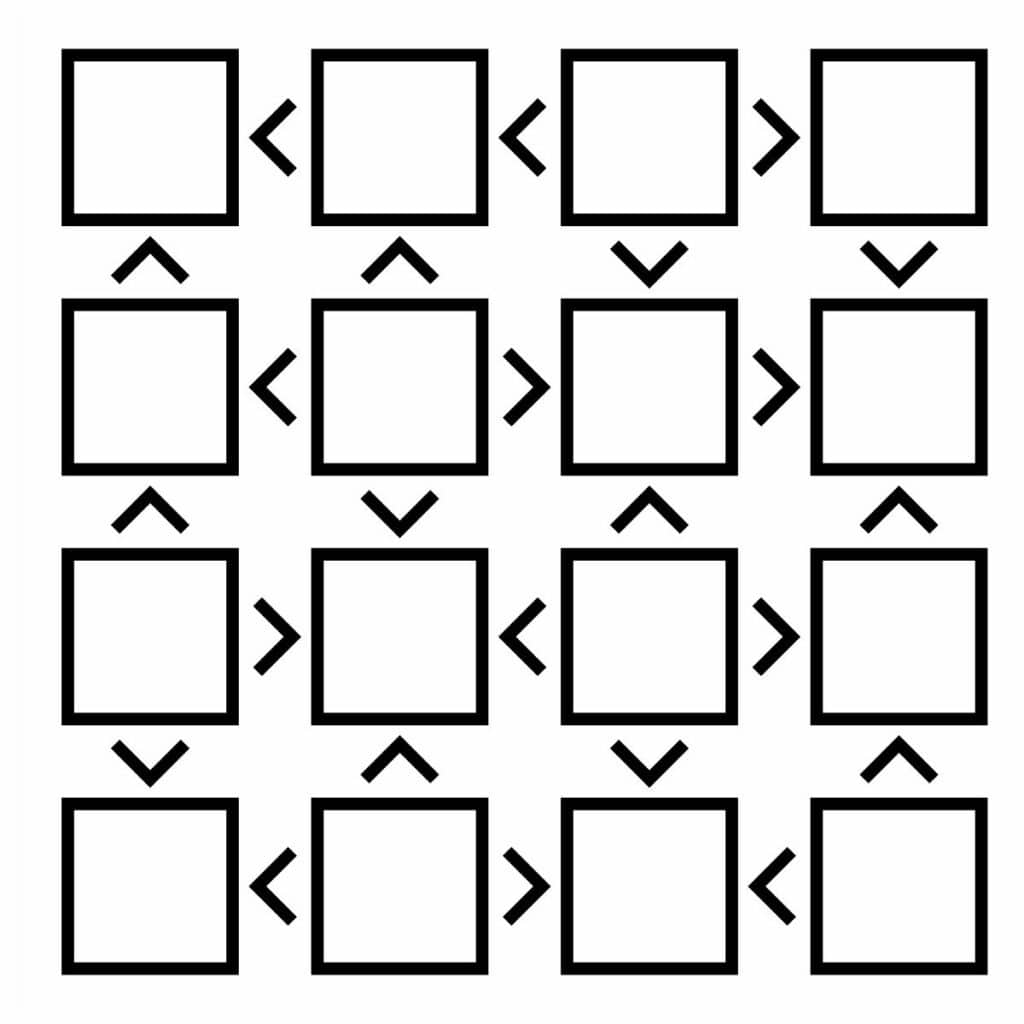
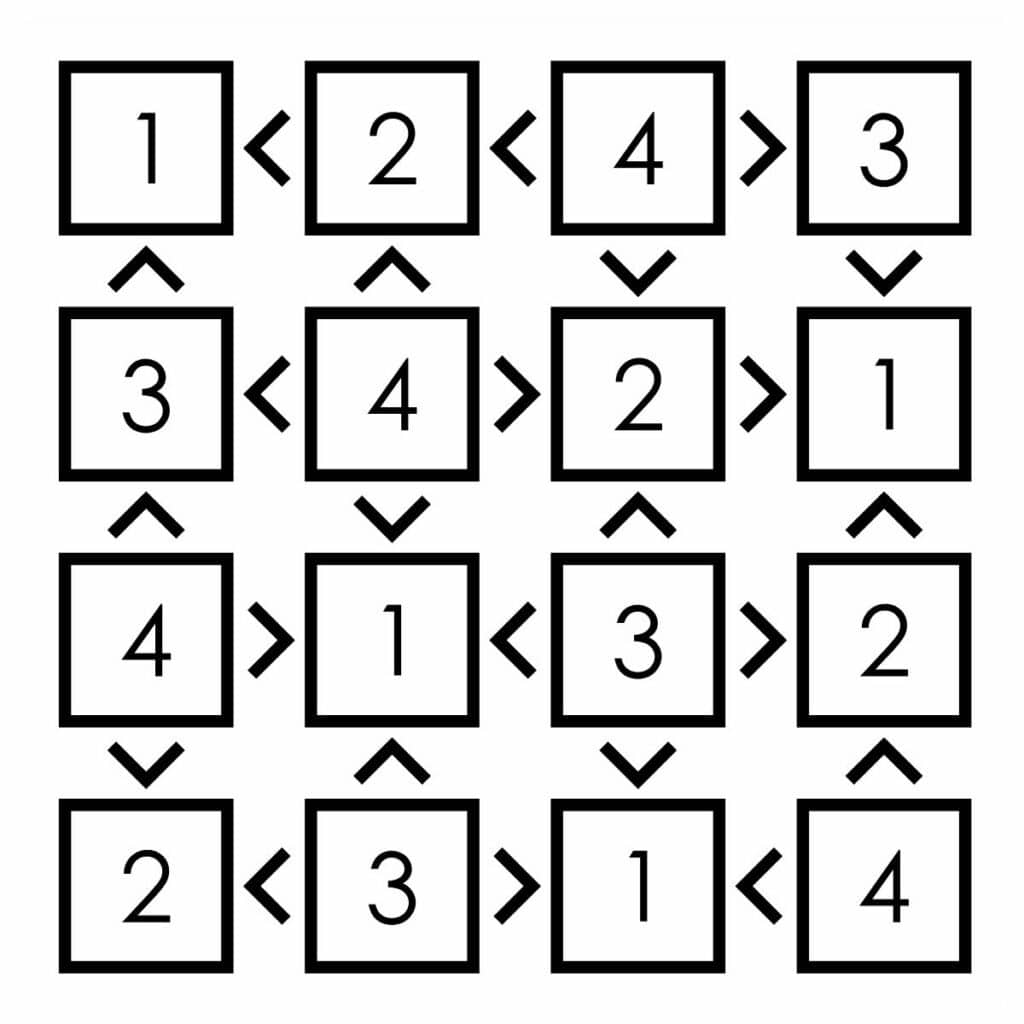
Using Futoshiki Puzzles in the Classroom
I was first introduced to futoshiki puzzles in 2015 when Christine Mishra left a comment on an old blog post asking if I was familiar with these logic puzzles which involve inequality symbols. I was intrigued, and I immediately printed out a set of these puzzles to use in my classroom as a “Figure it Out Friday” activity.
These puzzles would make a great extension task while studying inequality symbols. Or put one up as a class opener to see how familiar your students are with inequality symbols at the beginning of your unit on inequalities.
Different Sizes of Futoshiki Puzzles to Print
I am working on creating a selection of free printable futoshiki puzzles for teachers to use in their classrooms in a wide variety of sizes and difficulty levels. These are available as a free pdf file.
Puzzle Solutions
Puzzle solutions are available on a password-protected solution page. I do not openly post the puzzle answer keys because one of my goals as a resource creator is to craft learning experiences for students that are non-google-able. I want teachers to be able to use these puzzles in their classrooms without the solutions being found easily on the Internet.
Please email me at sarah@mathequalslove.net for the password to the answer key database featuring all of my printable puzzles and math worksheets. I frequently have students emailing me for the answer key, so please specify in your email what school you teach at and what subjects you teach. If you do not provide these details, I will not be able to send you the password.
Not a teacher? Go ahead and send me an email as well. Just let me know what you are using the puzzles for. I am continually in awe of how many people are using these puzzles with scouting groups, with senior adults battling dementia, or as fun activities in their workplace. Just give me enough details so I know you are not a student looking for answers to the puzzle that was assigned as their homework!
Wow! These are great — thanks for making me discover them. You should do a post on Magic Squares, too (the greater-than equal signs were akin to the arrows used for direction in an odd magic square). Check this out: https://mathworld.wolfram.com/MagicSquare.html