Shikaku Puzzles
What are Shikaku Puzzles?
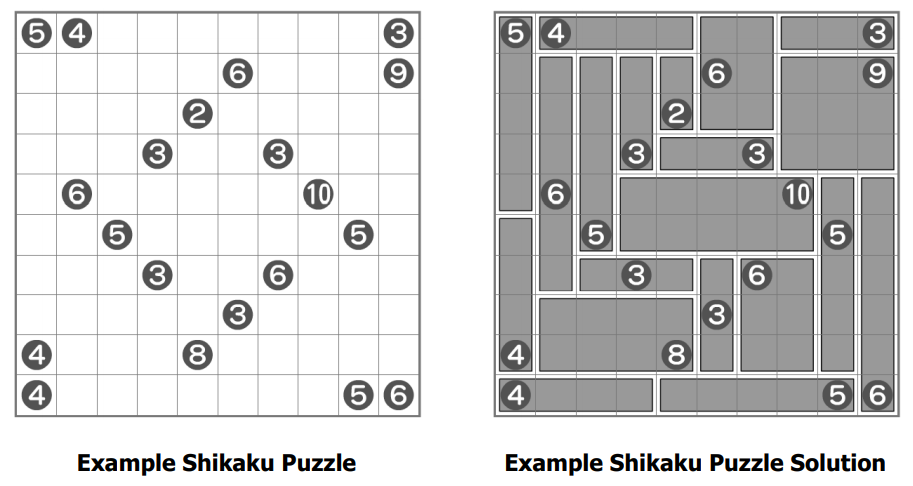
Shikaku Puzzles are a geometric-based logic puzzle from Japan. I was first introduced to them from a tweet from Bowen Kerins.
The goal of a shikaku puzzle is to subdivide the grid into rectangles (and squares) so that the number in each rectangle refers to the area of that rectangle. Only one number may appear in each rectangle. Additionally, no rectangles may overlap.
These puzzles can be tied to the mathematics curriculum in multiple ways. They are a natural fit for a unit on area. They also make a great tie-in to prime vs composite numbers.
I find that my students who enjoy Hidato Puzzles also really enjoy these shikaku puzzles.
My initial research of shikaku puzzles led me to an article by Dr. Jeffrey J. Wanko in NCTM’s Mathematics Teaching in the Middle School May 2010 issue. If you don’t have an NCTM membership to view this article, I found a copy uploaded online here.
Introducing Shikaku Puzzles to Students
Dr. Wanko wrote about a process of introducing students to logic puzzles by first showing them a completed puzzle and having them determine the rules of the puzzle.
I tried this out the first time I introduced these puzzles to students, and I found it to be a very successful method.
I placed the unsolved shikaku puzzle from the article on the SMARTBoard. I asked students to speculate as to what the rules of the puzzle were.
After a few suggestions, I asked students if it would help to see a completed puzzle. They were eager to see this.
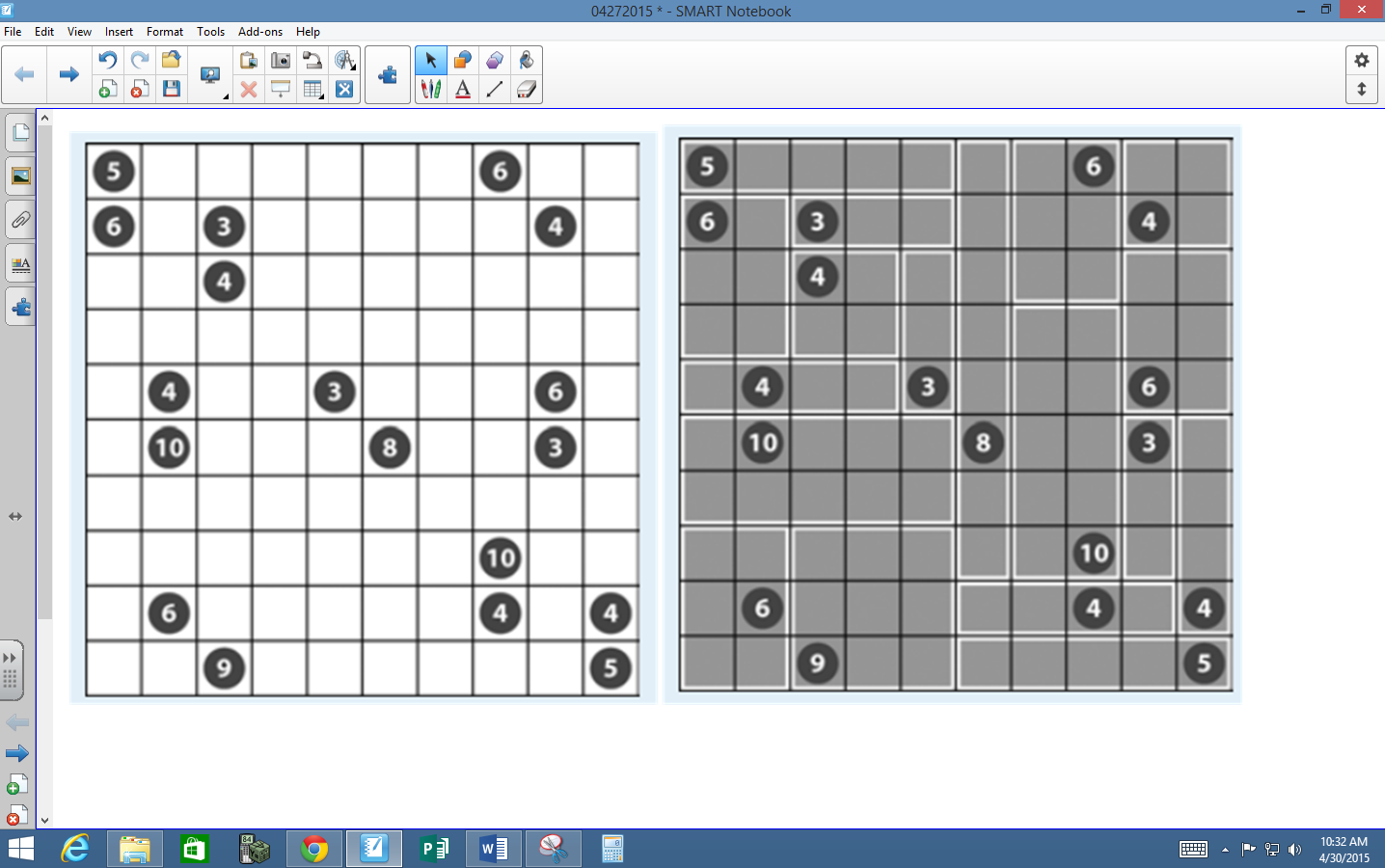
At first several students proclaimed that this was too hard or impossible. And, of course, I followed this up with “This will take some time and effort.” In some class periods, a student said this second line instead of me.
Yay for growth mindset! It was really cool to see the light bulbs going off as students studied the screen. Soon, they decided that the circles told how many boxes were in each section.
Though, the room quickly erupted when one student claimed that each section must be a rectangle. Other students argued that squares were also allowed.
Some students claimed that every square was a rectangle. Several classmates were less than convinced.
We also discussed the fact that the rectangles could not overlap, and the circle could be placed anywhere in the rectangle. With these rules, students were antsy to start a puzzle.
I put up a puzzle on the board to do as a class from the same NCTM article. Students came up one at a time and drew a rectangle where they thought it went. Some students were not using logic to place their rectangles.
But, I didn’t say a word. I figured the class would figure this out eventually. And, they did. They worked together to fix the mistakes.
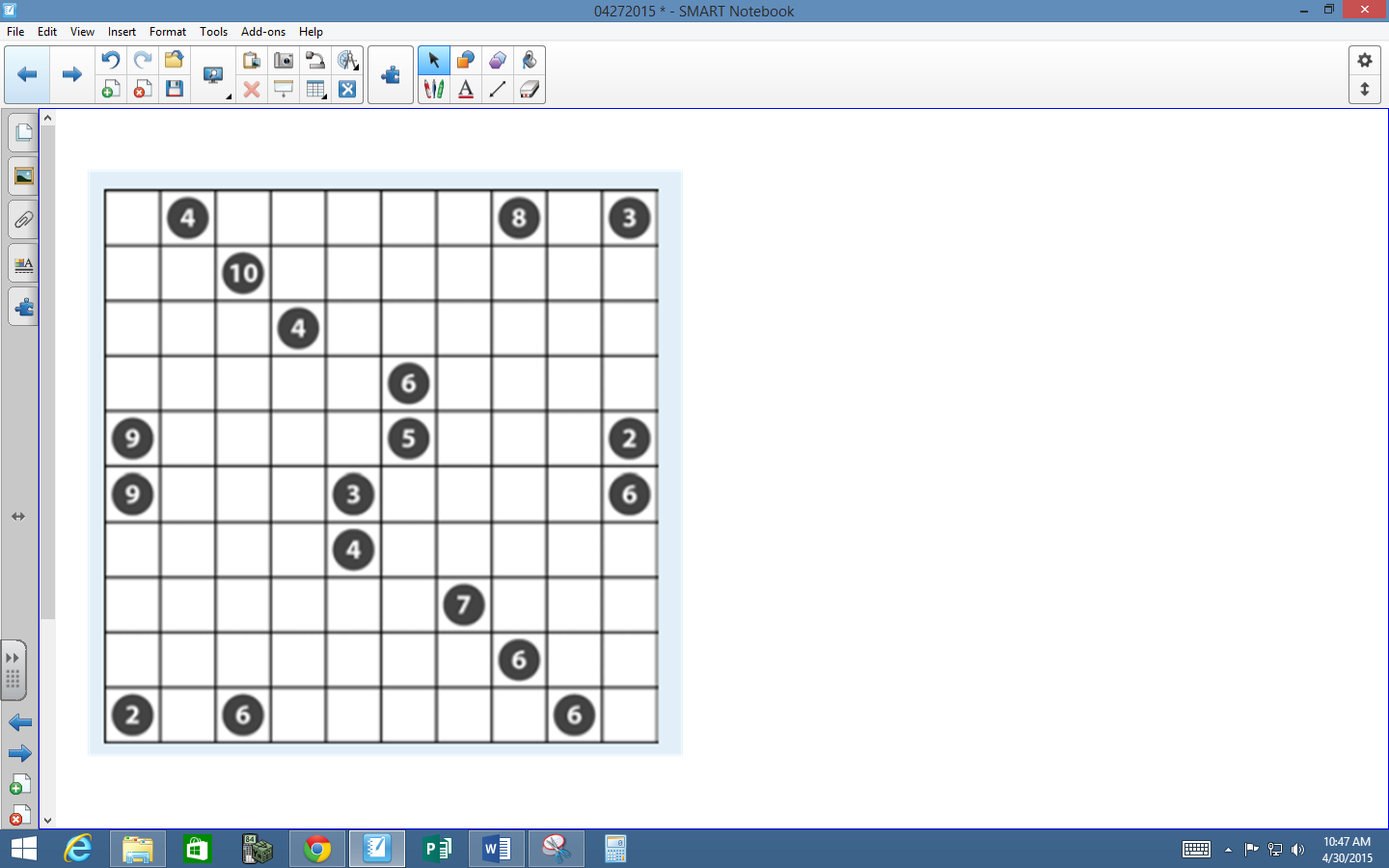
After doing one puzzle as a class, I gave students the activity sheet from the NCTM article with 4 more shikaku puzzles. To receive their points for the day, they had to successfully complete two of the puzzles.
Most of the students agreed that they liked these puzzles better than the griddler puzzles from the previous day.
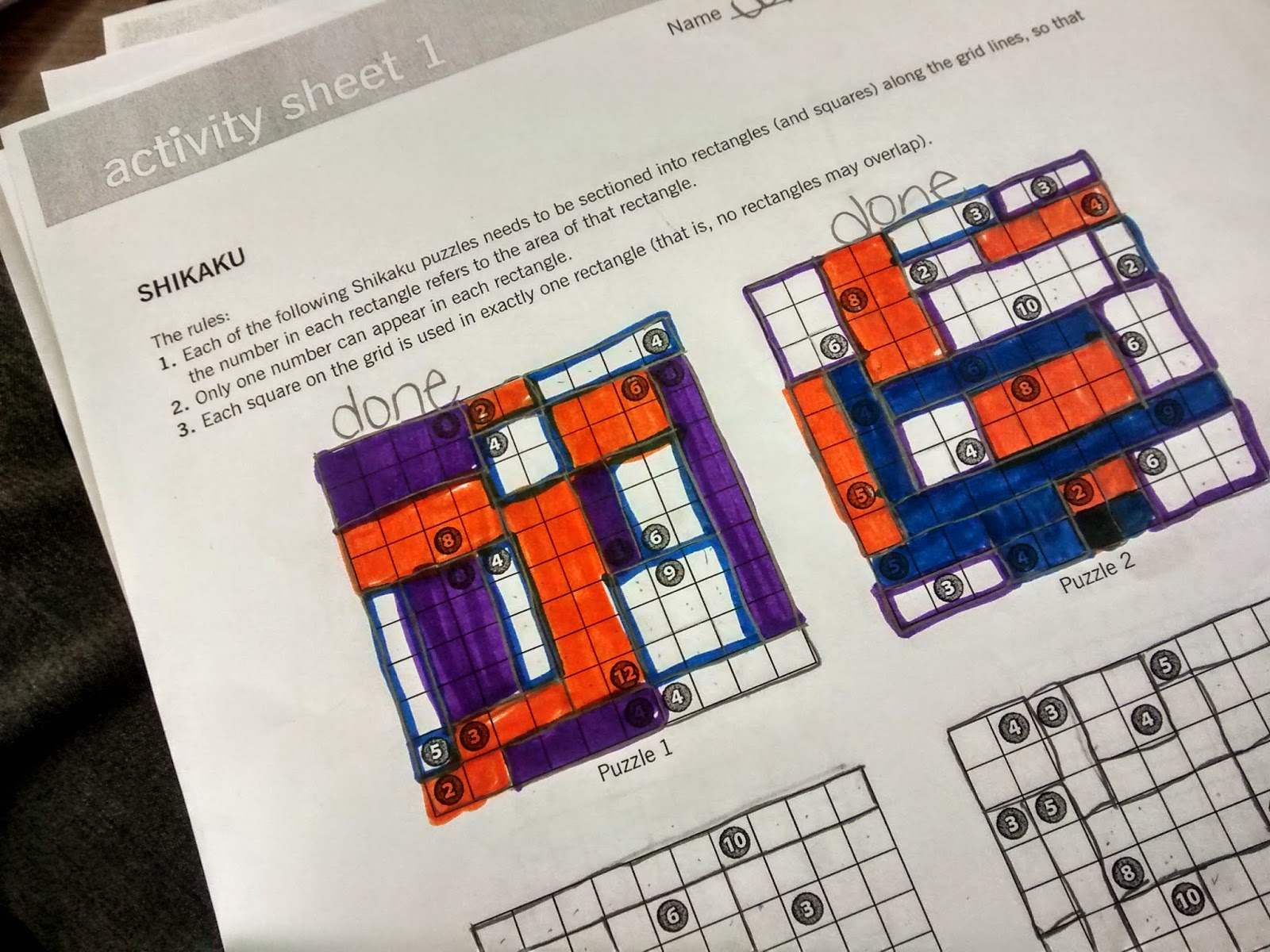
It was eye-opening to listen to students’ thinking as they worked these puzzles. One student claimed that if the circled number was odd, the boxes would always be in a straight line.
I hope they eventually realized that 9 broke this pattern. What they were actually noticing was the difference between prime and composite numbers!
These got my students thinking which is exactly what I want them to be doing during these last few weeks after testing and before the end of school. Several students came in the next day and asked for more of these puzzles to do.
I even have students who aren’t enrolled in my classes coming to me and asking for logic puzzles because they see their friends doing them. These puzzles are definitely a keeper!
Free Shikaku Puzzle Downloads
Shikaku Puzzles from Dr. Jeffrey Wanko
Want to do shikaku puzzles with your students? Dr. Jeffrey Wanko (the author of the NCTM article I mentioned above) has a free collection of shikaku puzzles (as well as several other Japanese logic puzzles) on his website.



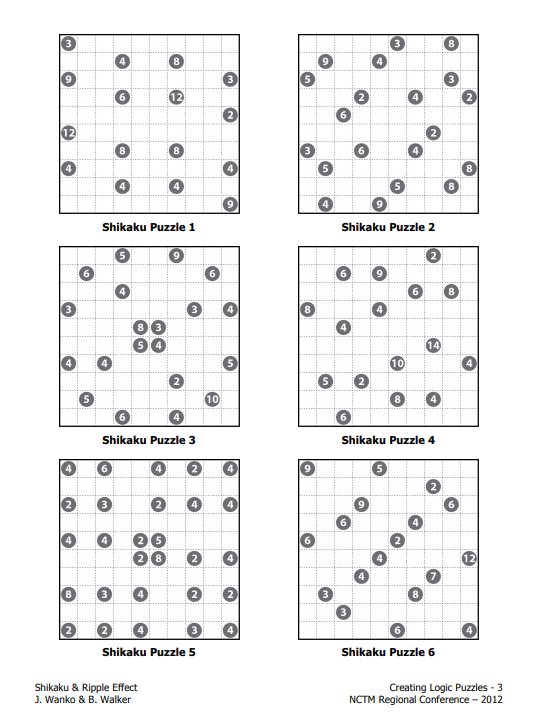
If you are looking for smaller shikaku puzzles, Dr. Jeffrey Wanko has you covered. He has another collection of shikaku puzzles from a 2012 NCTM Presentation.
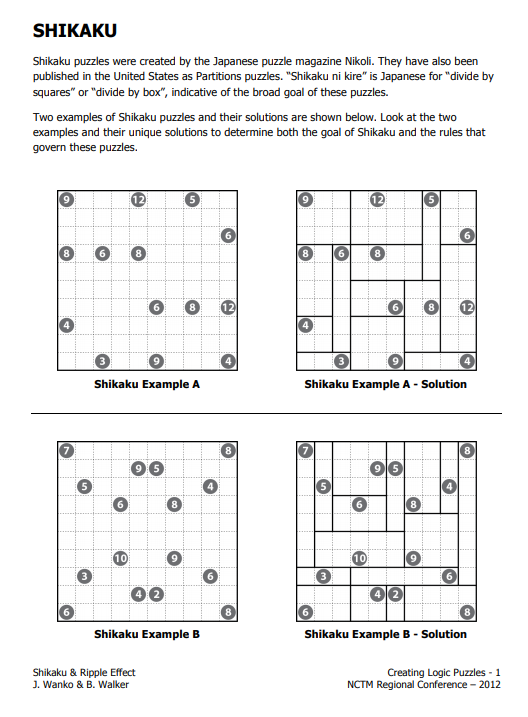

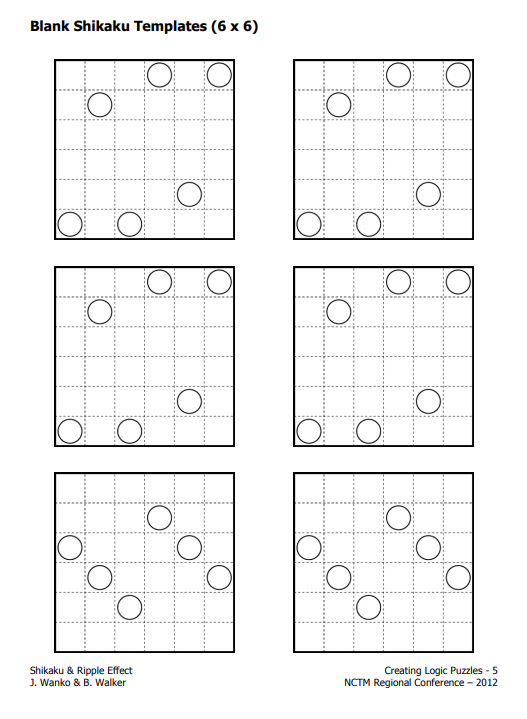
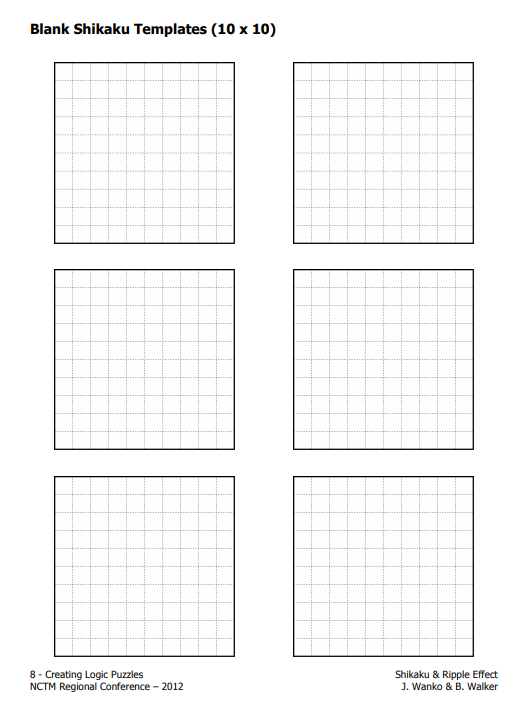
This file also includes several different 6 x 6 and 10 x 10 blank shikaku templates so you or your students can create your own shikaku puzzles.
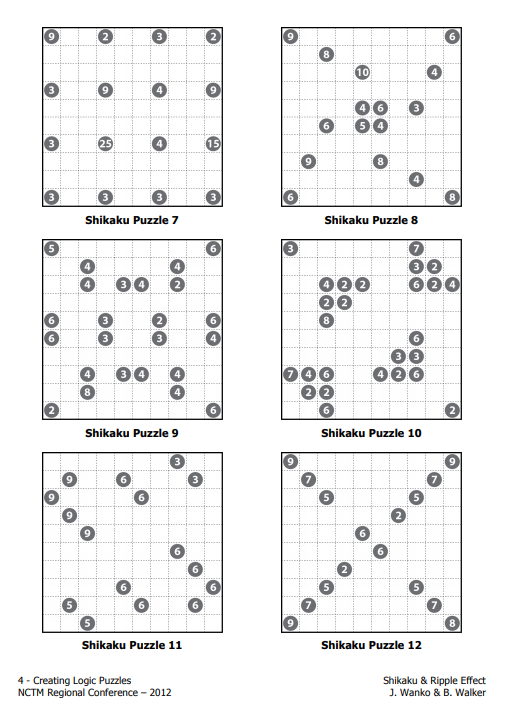
Looking for even more shikaku puzzles? I also found these two handouts with two weeks worth of shikaku puzzles for students to tackle.
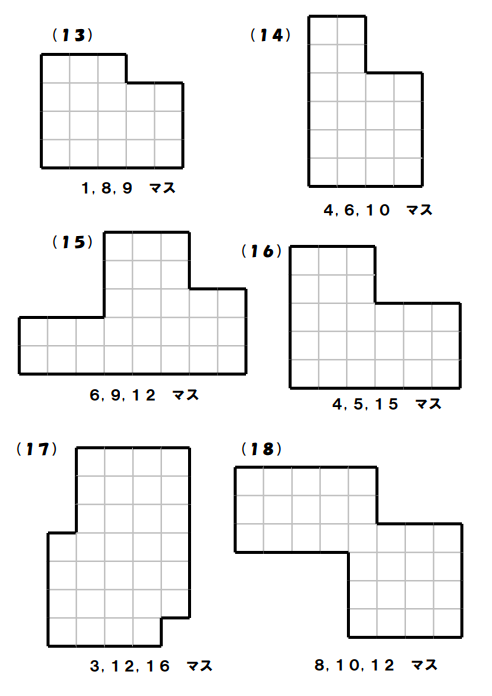
Shikaku Puzzle from Naoki Inaba
Naoki Inaba has created his own set of free shikaku puzzles. They are slightly different than the puzzles shared above since the puzzle grids are not all squares and rectangles.
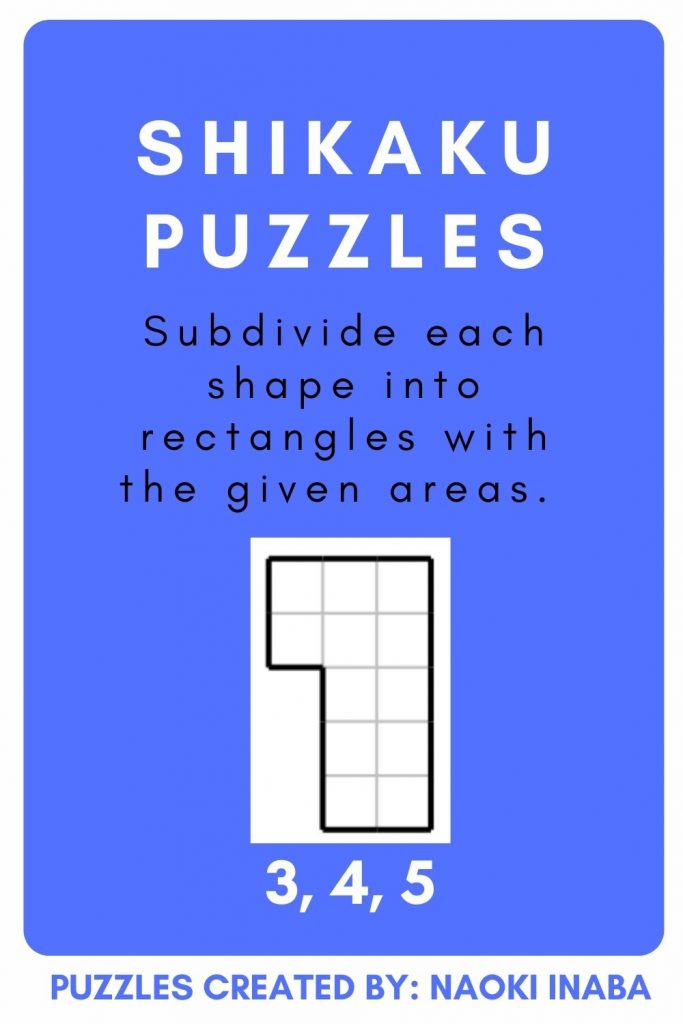
Instead of putting the numbers in the grid, the numbers are placed below the puzzle to tell you how to sub-divide the grid.
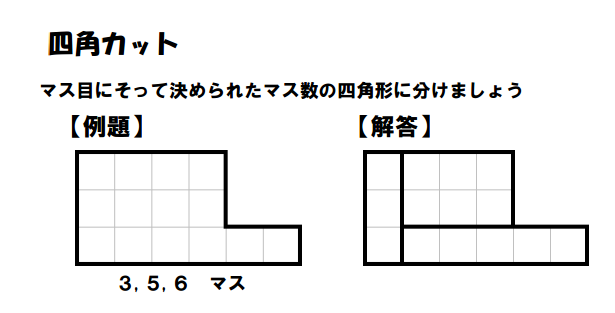
This PDF file from Naoki Inaba contains 42 of these shikaku puzzles which get progressively harder. Solutions are posted here.
Miscellaneous Printable Shikaku Puzzles
- Classics Collection
- TES – Free Download of Shikaku Workbook from Cubed Maths
- Science Mom Challenge
- Nikoli Hurdles
- Shikaku Puzzles from Puzzle Phil
- Play Shikaku Online from Maths Resources
- Puzzle Bomb
- Shikaku Puzzle for Turkish Puzzle Championship
- 2010 Shikaku Puzzle
Variations on Shikaku
Shape Shikaku
Walker Anderson shares a variation on shikaku called shape shikaku. In a traditional shikaku puzzle, the grid must be divided into rectangles. In shape shikaku, part of the grid is divided into rectangles.
The rest of the grid is divided into a specified number of a specified shape.

Pentomino Shikaku
Pentomino shikaku is like regular shikaku except the grid must be divided into rectangles AND pentominoes.
Shikaku with Gray Cells
In this version of shikaku, gray cells do not count! Here’s another set.
More Printable Paper and Pencil Logic Puzzles
- Blank Sudoku Grid Printable
- Sixes Number Challenge
- 3-1-4 Pi Day Number Challenge
- Sankaku Puzzles
- Strimko Puzzles in the Classroom
- Square Sudokus
- Make It Pythagorean Puzzles
- Number Ball Puzzles by Naoki Inaba
- Hidato Puzzles
- Step Puzzles by Naoki Inaba – A Logic Puzzle for Introducing Arithmetic Sequences
- Kazu Sagashi Puzzles from Naoki Inaba
- Factor Tree Puzzles Inspired by Dr. Harold Reiter
- Strimko Logic Puzzles Review
- Tents and Trees Puzzles
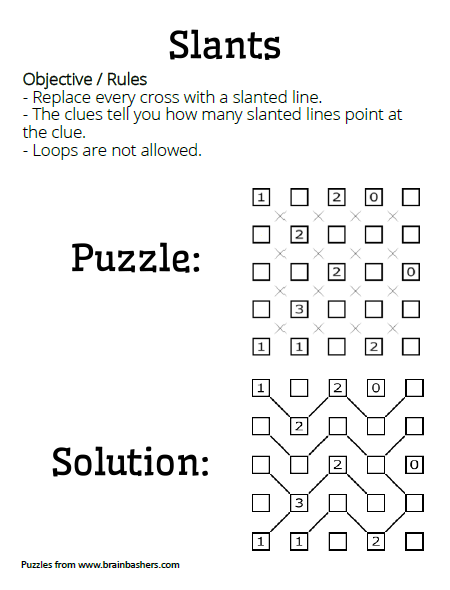
- Slants Puzzles
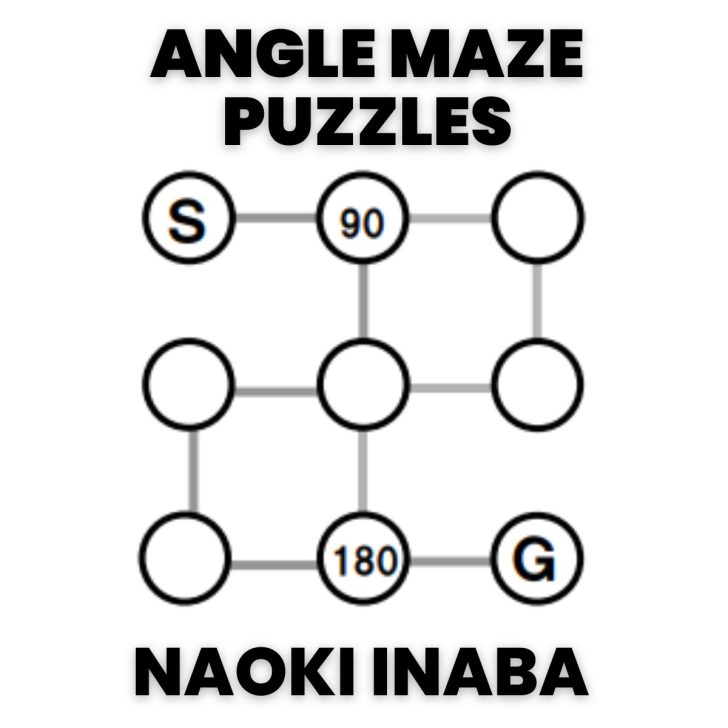
- Angle Mazes by Naoki Inaba
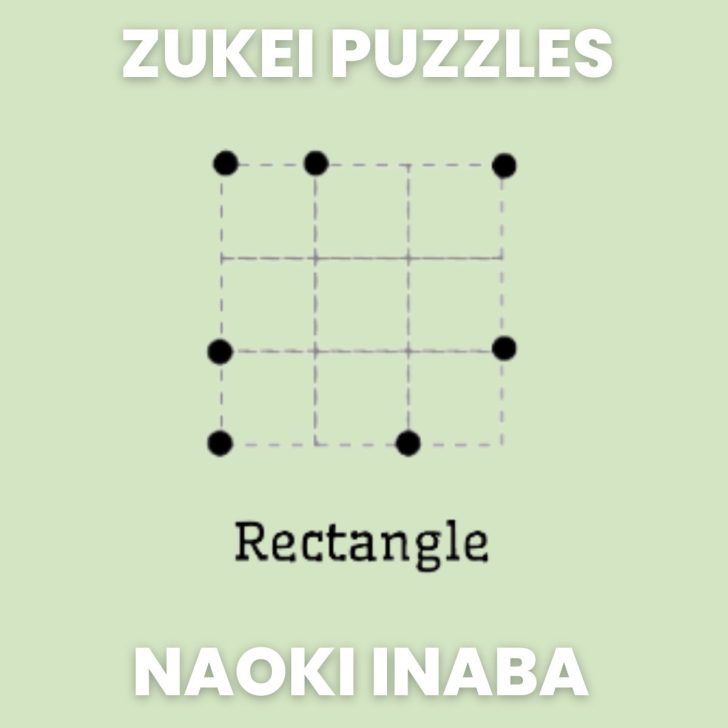
- Zukei Puzzles
- Japanese Logic Puzzles for the Secondary Math Classroom
- Area Maze Puzzles from Naoki Inaba
- Masyu Puzzles
- KenKen In The Classroom
- Futoshiki Puzzles
- Hashi Puzzles
- Shikaku Puzzles
- Nonogram Puzzles
- Digit Cells Puzzle























I have never seen these before! This is going to be part of my last week of school with the kids. Thanks again for everything you share:)
Hope your students love them as much as mine did!
My students had their End of Course Exam last Thursday and Friday, and like you, I think these last two weeks before the end of school are an excellent time to get my students convinced we are doing something "just for fun" while really introducing them to topics in mathematics that I don't usually get to teach. I have loved the logic puzzles you have posted (four fours was my fave!), but my students really took to the shikaku puzzles today! I handed out the same sheet of four puzzles, and had a handful of students ask me about 30 minutes through the class period if I had any others or more challenging versions because they had already finished the first four!
If you haven't heard about similar logic puzzle work from The Space Between the Numbers, I'd suggest looking around her blog! One starting point would be https://betweenthenumbers.wordpress.com/2010/10/17/puzzle-presentation/
Thanks for the link!