Number Ball Puzzles by Naoki Inaba
Today I want to share a new puzzle I’ve been playing with for the last few days: Naoki Inaba‘s Number Ball Puzzles.

The other day, I set out to try to bring some semblance of order to my puzzles folder on my laptop. This is the place on my computer where I keep PDFs of all the different types of logic puzzles I have come across over my years of browsing the internet. I started collecting these puzzles in college, and I still get excited when I run across a new type of puzzle that I have never seen before.
In this folder, I found a collection of puzzles that I had downloaded from Naoki Inaba’s amazing website (that happens to be written in Japanese). I had planned to run these puzzles through google translate, but I apparently got distracted and promptly forgot about my intended task. I had put a few of these puzzles in a folder named “To Try.” Since we’ve been stuck at home due the ice/snowpocalypse, I decided to print out a set of these puzzles and give them a try.
The first new type of Naoki Inaba puzzle I tried is called Number Ball (ナンバーボール). In this puzzle, you are presented with a square grid. Some of the squares contain numbers in circles. Other squares contain empty circles or x’s.
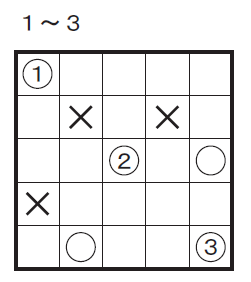
Here’s my translation of the original Japanese rules: Each row and column must contain balls with one of each of the numbers in the given range. Squares containing a circle must be used. Squares containing an x may not be used.
Inaba provides an example of a puzzle and its solution to help ensure that you understand the rules before beginning.
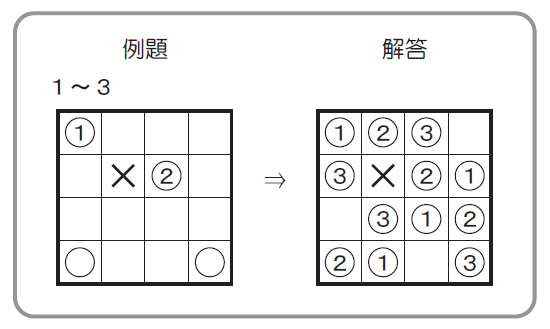
I was really hoping that I had discovered a new type of puzzle to use in my classroom with my math students. Then, I tried to solve the puzzles myself. I found them much harder than I expected. On my first day of puzzling, I managed to solve exactly ONE of the number ball puzzles. Of the five puzzles provided by Inaba, I could only work out a solution to the SMALLEST puzzle.
The next night after the toddler was put to bed, I pulled my clipboard of puzzles back out. This time, I was able to solve the next three puzzles. But, the last and largest puzzle proved to be a huge stumper. I tried several methods of solving it and ended up doing a lot of erasing and starting over in hopes that I would find some sort of clue that I had overlooked.
Tonight, I decided to have one more go at solving these number ball puzzles. I thought that maybe I had overlooked some strategy in solving the smaller puzzles that I needed to solve the largest puzzle.
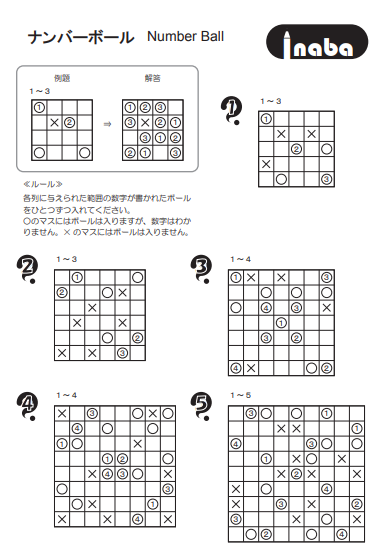
I printed off a fresh set of number ball puzzles. Then, I set about to resolve the puzzles I had previously solved the previous two nights. I did make one slight change. I started by solving the small example puzzle that Inaba had originally provided a worked solution for. I made my way through each of the previously solved puzzles. My experience made the puzzle solving much smoother, but I still found them to be quite tricky at times.
Then, I tackled the largest puzzle. Halfway through solving it, I had an epiphany that ended up helping me break through my puzzle solving roadblock.
I really enjoyed solving these puzzles, but I think there are many other puzzles by Naoki Inaba that are more suitable for use in the secondary classroom. Still, I am sharing my English translation of these puzzles here on my blog in case you want to try your hand at solving these yourselves. I found them a very satisfying puzzle to solve. I think you will, too.
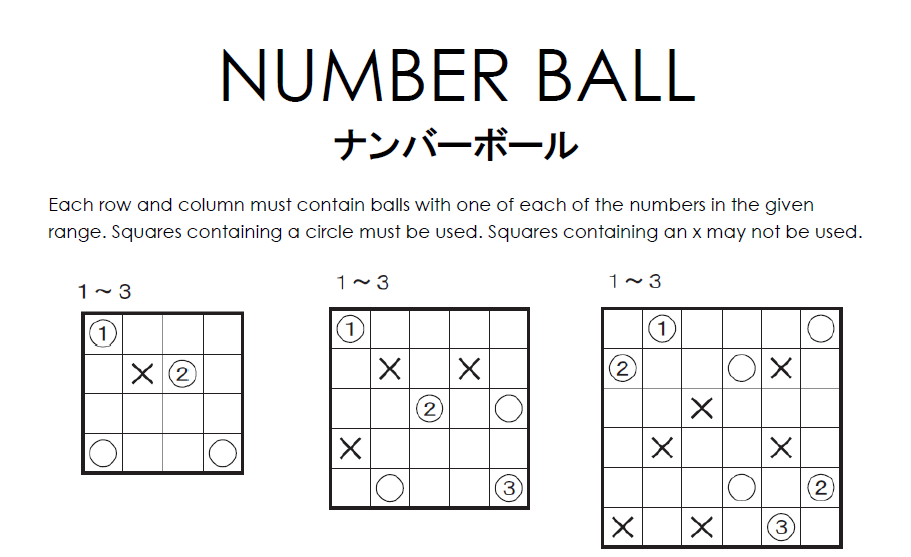
Instead of including a worked example like Inaba did in his PDF of the puzzles, I have placed the example puzzle as the first puzzle to be solved.
If you do want to try these with kids, I think the first two puzzles are quite accessible to students. The third and subsequent puzzles will likely give your students much frustration. Though, maybe they will discover a solving method that I somehow overlooked? I have a feeling my students will take their normal approach to solving such puzzles and bypass the logical thinking step to jump straight into writing random numbers into boxes…

I would like to emphasize that you should try these puzzles out yourself BEFORE using them with students! These puzzles are difficult, but they are not impossible. Productive struggle is a good thing. You need to know your students and how much struggle is productive and how much struggle is overwhelming/crippling.
Free Download of English Translation of Naoki Inaba’s Number Ball Puzzles
Number Ball Puzzles by Naoki Inaba (PDF) (1244 downloads )
Number Ball Puzzles by Naoki Inaba (Editable Publisher File ZIP) (770 downloads )
Want more puzzles like this? Check out this page where I have collected many of Naoki Inaba’s inspiring math puzzles.
More Printable Paper and Pencil Logic Puzzles
- Blank Sudoku Grid Printable
- Sixes Number Challenge
- 3-1-4 Pi Day Number Challenge
- Sankaku Puzzles
- Strimko Puzzles in the Classroom
- Square Sudokus
- Make It Pythagorean Puzzles
- Number Ball Puzzles by Naoki Inaba
- Hidato Puzzles
- Step Puzzles by Naoki Inaba – A Logic Puzzle for Introducing Arithmetic Sequences
- Kazu Sagashi Puzzles from Naoki Inaba
- Factor Tree Puzzles Inspired by Dr. Harold Reiter
- Strimko Logic Puzzles Review
- Tents and Trees Puzzles
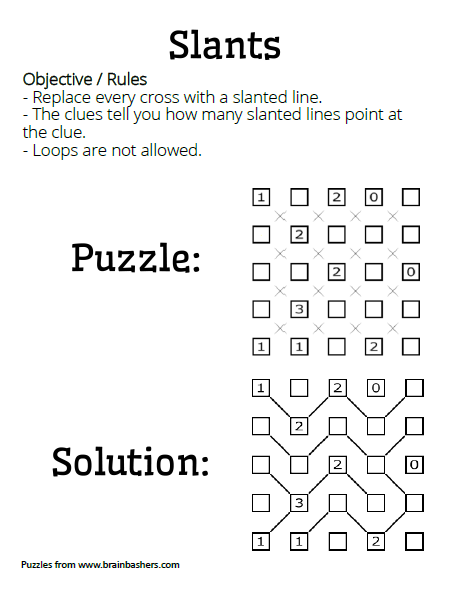
- Slants Puzzles
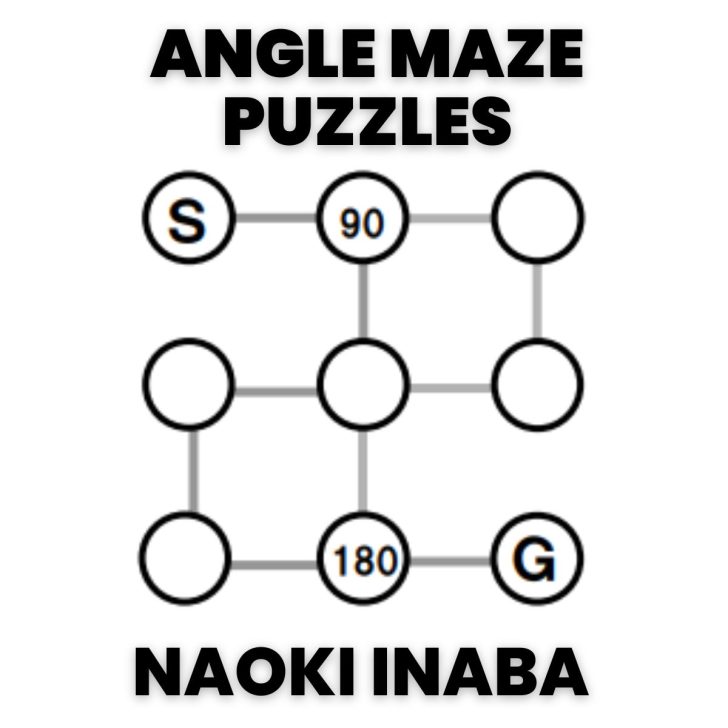
- Angle Mazes by Naoki Inaba
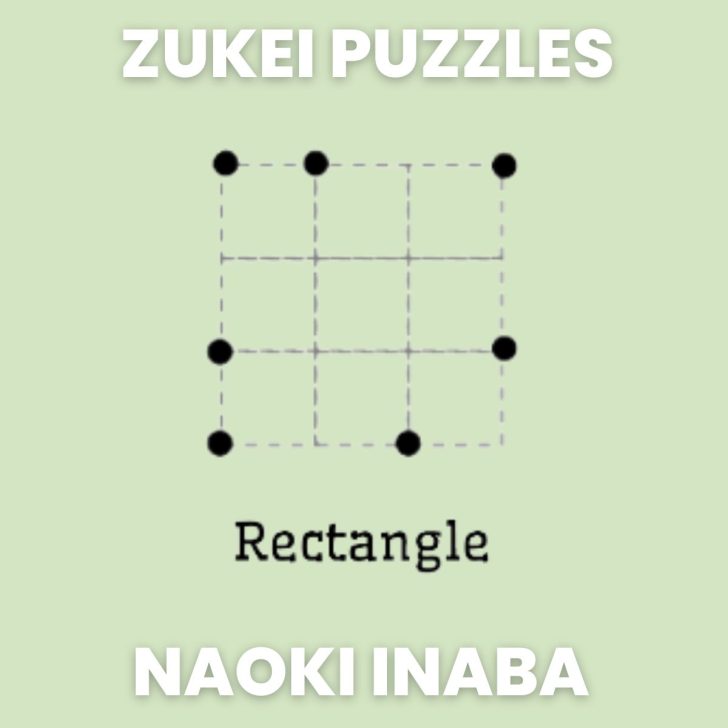
- Zukei Puzzles
- Japanese Logic Puzzles for the Secondary Math Classroom
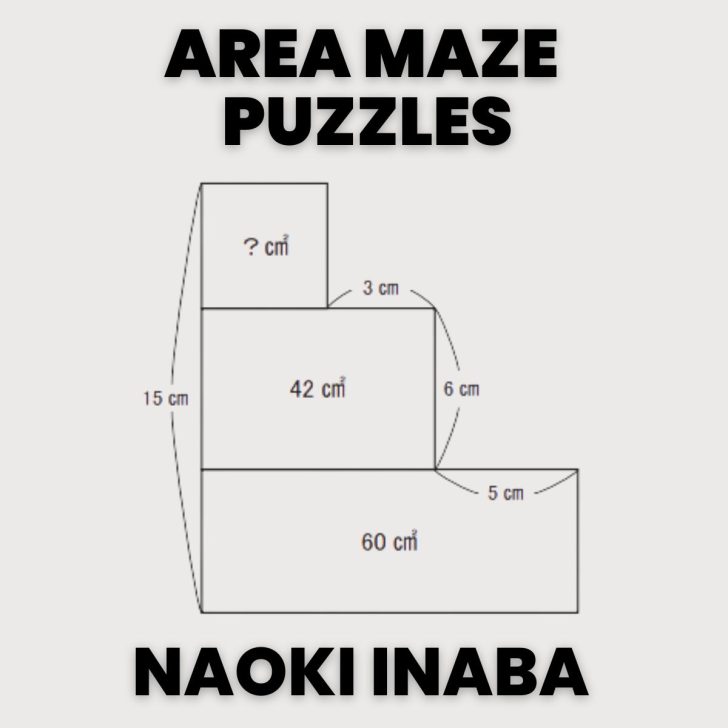
- Area Maze Puzzles from Naoki Inaba
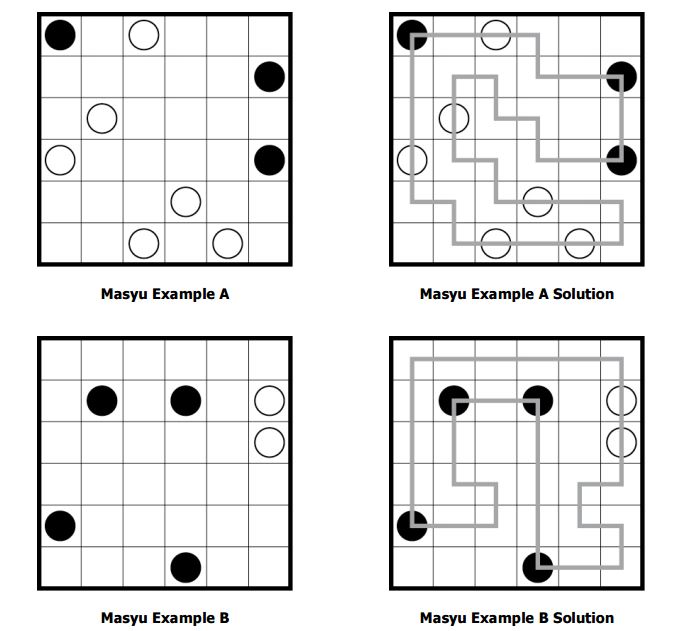
- Masyu Puzzles
- KenKen In The Classroom
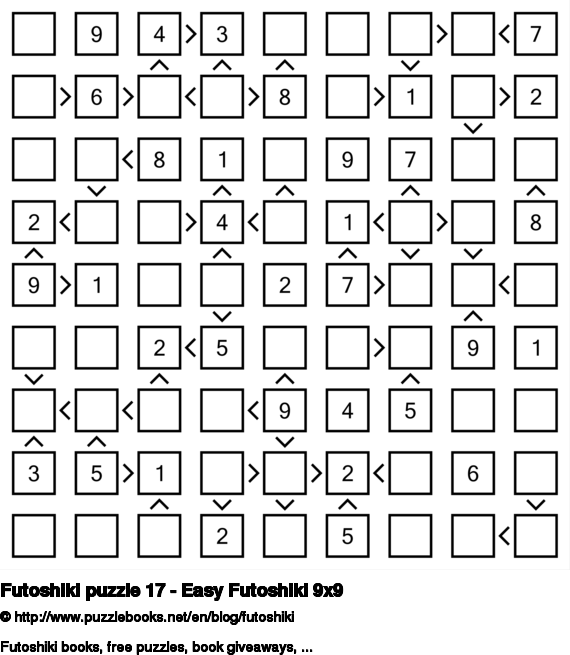
- Futoshiki Puzzles
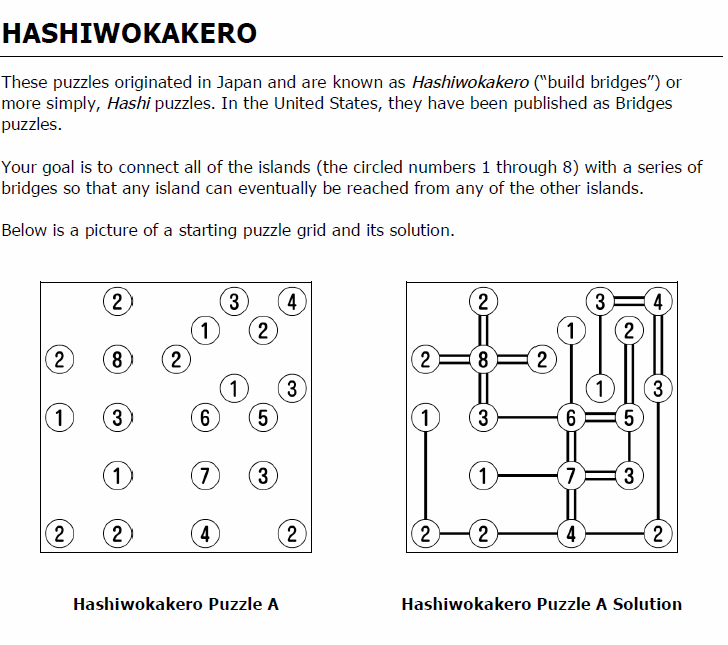
- Hashi Puzzles
- Shikaku Puzzles
- Nonogram Puzzles
- Digit Cells Puzzle










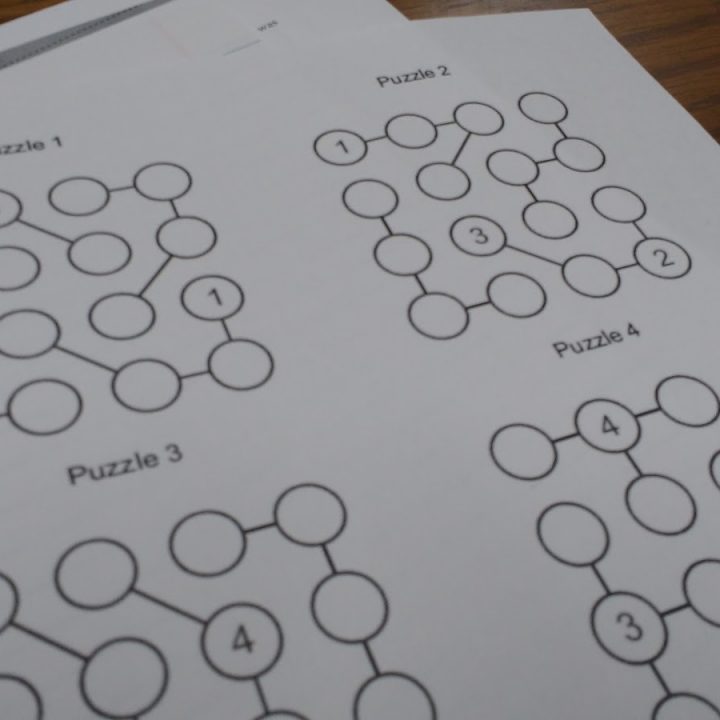











Unless I’m missing something obvious, these puzzles are similar to some I’ve been playing on Sporcle—except these are numbers instead of letters. I’ve been solving them by writing all the possible answers for each square. Eventually, I find one square that can only be one letter and the rest of the rows and columns fall into line.
https://www.sporcle.com/playlists/dvsdab/abcd-grids