Japanese Logic Puzzles for the Secondary Math Classroom
This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.
Recently, I posted about some awesome area and volume puzzles created by Naoki Inaba. You can read that post here. While researching those puzzles and looking for possible online sources for them, I found some on Mr. Inaba’s website. This led me to start wondering, “What kind of other puzzles has he created?”

So, ever-curious me, decided to visit the rest of the website. Of course, it’s all written in Japanese. But, with enough random-clicking, I was able to stumble across some more math-y logic puzzles that I can’t wait to incorporate in my math classroom. The instructions are in Japanese, but the math of the puzzle is universal.
So, let’s play a game. Here are the rules:
- I’ll post a picture of a puzzle and the solution. The instructions are in Japanese.
- Determine the goal of the puzzle.
- Figure out how you could use it in your math classroom.
- Scroll down and see if your thoughts match mine!
Sound fun? Let’s Begin!
These are all original puzzles created by Naoki Inaba and posted for free on his website.
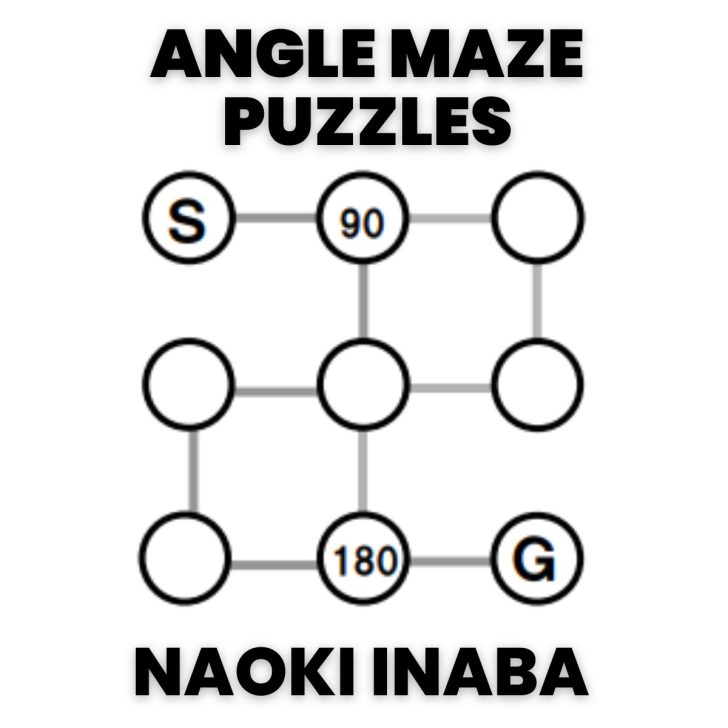
K-Maze Puzzles
Inaba calls these K-Maze Puzzles.
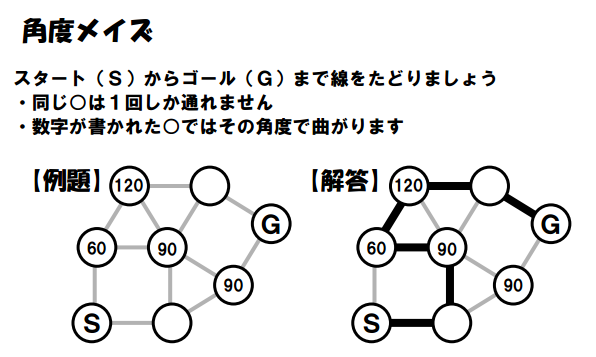
From my puzzle-studying, I’ve determined that these are angle puzzles. S stands for Start. G stands for Goal. Draw a path from S to G so that the path passes through each circle with the angle measure specified by the puzzle.
Google Translate translates this as “Angle Maze.” The PDF file of these puzzles contains an example of a wrong solution. So, I’m also assuming that you can only travel through each circle once.
This PDF contains 38 of these puzzles which get progressively harder. Here are the solutions.
If you like this sort of angle puzzle, Inaba also has a different version where you’re not told where to start or end. Instead, you’re just told exactly which points you MUST go through. You can find four of those puzzles here.
I think these would be a great warm-up for a geometry class!
UPDATE: I have now written an entire blog post about these angle maze puzzles!
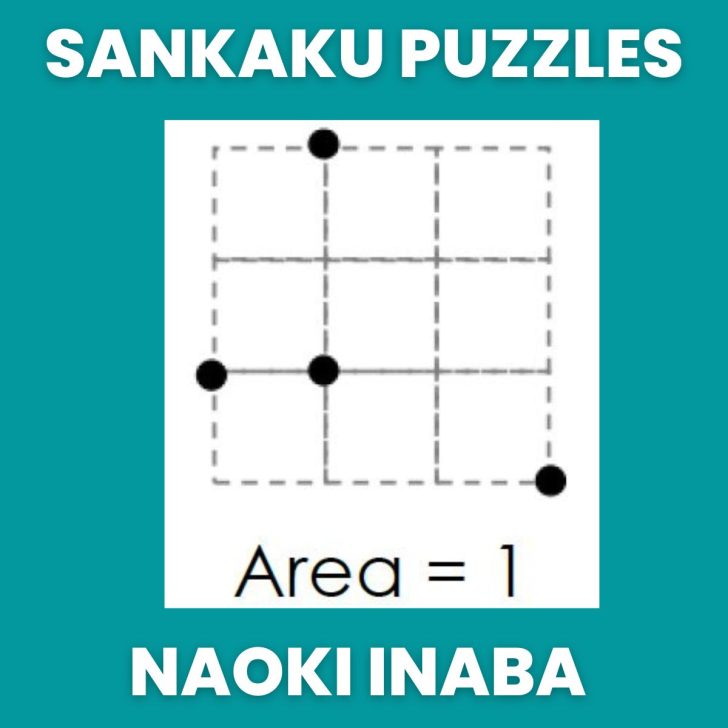
Sankaku Puzzles
Inaba calls these Sankaku Puzzles.
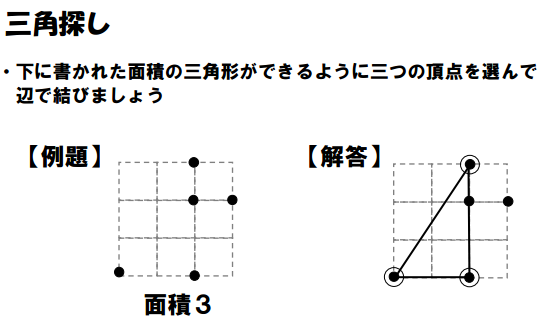
These are area puzzles. See that number 3 next to those characters? That tells you to make a triangle that goes through a subset of those points with an area of 3.
I think the associated instructional images in the PDF file for these puzzles are beautiful. I’m not going to insert them here because I really do want you to go and check them out!
Google Translate translates this puzzle title as “Looking Triangle.” Not quite sure what that’s about…
The PDF file provides you with 42 of these to keep you (or your students) busy. There are also solutions so you can check your work along the way. Since the directions are in a foreign language, I try to check my work with the solutions A LOT just to make sure I haven’t made any wrong assumptions about the rules of the puzzle.
These would be great for practicing/reviewing finding the area of a triangle.
Kazu Sagashi Puzzles
Inaba calls this puzzle “Kazu.”
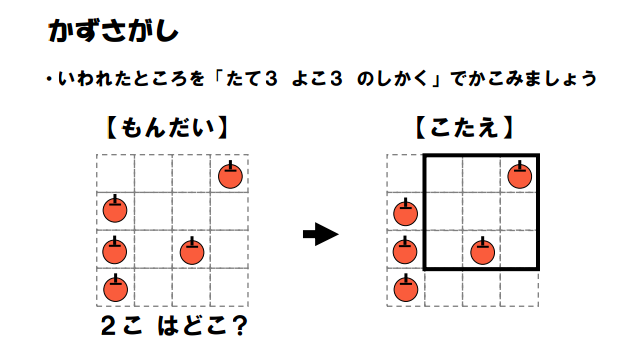
I have to admit, these puzzles are a bit trickier for me to decode. See that 2 below the puzzle? That tells you that you need to create a square that holds exactly 2 apples. I thought they were pumpkins at first, but Google Translate told me otherwise. As for the title of this puzzle, Google Translate says it’s “Looking for Kaz.”
You also need to know that your square must be 3 x 3. How are you supposed to know that? If you look closely at the text above the puzzles, you’ll see the number 3 appear twice.
The PDF file for this puzzle contains 42 different puzzles, but I’ve only figured out how to solve the first 24. Starting with puzzle 25, there are apples and oranges in the puzzles. And the numbers go away. If someone figures out how to do the later puzzles, please let us know in the comments below! If you want to check your assumptions, here are the solutions.
UPDATE: I have now written an entire blog post about these Kazu Sagashi Puzzles.
I think these puzzles would make a great warm-up. They would also be great to put inside a dry erase pocket and give to students who finish early and need something to keep their brains stimulated.
MATH = LOVE RECOMMENDS…

I cannot imagine teaching math without my dry erase pockets! They instantly make any activity more engaging and save me countless hours at the copy machine since I can use the same class sets of copies year after year.
Here are my current go-to recommendations:
If you don’t have a classroom set of dry erase pockets, you could also use heavy duty sheet protectors. But, I highly recommend investing in a classroom set of the pockets since they are so much more durable.
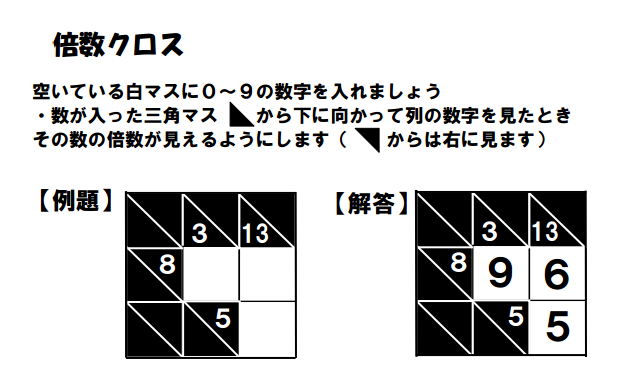
B-Cross Puzzles
Inaba calls this puzzle “B-Cross.” Google Translate translates the Japanese as “Multiple Cross.”
From what I can tell, this is a puzzle to practice factors and multiples. 8 is a factor of 96. 3 is a factor of 9. 13 is a factor of 65.
This PDF file contains 42 of these puzzles. The puzzles range from having 2-4 cells to fill in. Solutions are found here.
These would be great in any unit that deals with factors or multiples. You could also easily put up one of these as a do-now.
Blink Puzzles
Inaba calls these “Blink” puzzles. Google Translate changes the Japanese to “Multiple Link.”
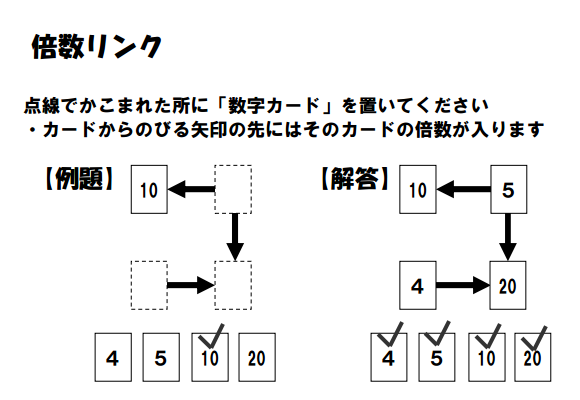
This is another puzzle that deals with factors and multiples. 5 points to both 10 and 20 in the solution, and 5 is a factor of both 10 and 20. 4 points to 20, and 4 is a factor of 20. The numbers you can choose from to put in each box are listed below. The number that has already been placed in the puzzle has a check mark above it.
This PDF file has 42 of these puzzles to solve. Here are solutions, too.
Like pretty much all of the puzzles on this page, this would make a great warm-up or brain break.
Mizu Puzzles
Inaba calls this puzzle “Mizu.” Google Translates changes the Japanese to “water so to water.” Yeah…
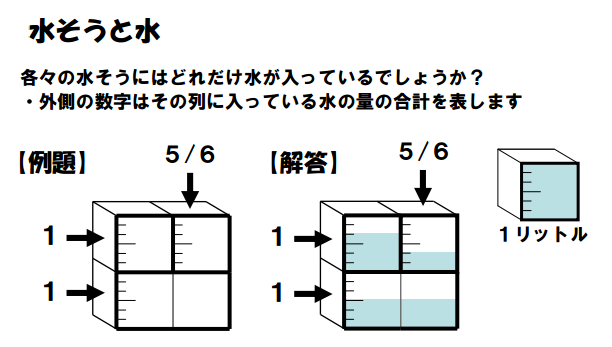
These are fraction puzzles, and I ADORE them! Seriously, I printed them off and work through all but the last page of them with a pink highlighter. Each small box counts as a single unit, 1. The arrows on the left tell you that the fractions in the top row and the bottom row should both add up to 1. The 5/6 on the top tells you that the fractions in the right column should add up to 5/6. Water is contained inside each set of thick black lines.
This PDF file contains 42 of these puzzles. And, here are solutions. Now that I’m looking at the solutions file, I realize that the last page of puzzles wasn’t as scary as I made it out to be. So, if you do the puzzles yourself, do yourself a favor and take a peek at how the solutions write up the last page before you drive yourself insane trying to do them the way you did all the previous pages.
These would make a perfect review of fractions. I found myself making a lot of equivalent fractions as I was solving these myself. I also had to do lots of fraction addition and subtraction in my head.
Shikaku Puzzles
Inaba calls these “Shikaku” puzzles. Google Translate changes the Japanese to “Square Cut.”
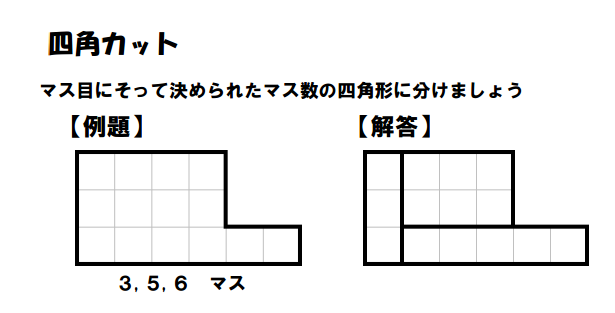
I’ve actually written about shikaku puzzles before, but they looked much different than these.
These are basic area puzzles. The numbers below each shape tell you to divide the shape up into rectangles with areas 3, 5, and 6. You might have to remind students that squares also count as rectangles. This always trips up at least a few kids.
This PDF file contains 42 of these puzzles which get progressively harder. Solutions are posted here.
These would make a fun warm-up activity. I think they’re especially applicable when learning about prime and composite numbers. In the above puzzle, there is only one way to make an area of 3. It must be 3 x 1. (Assuming 1 x 3 and 3 x 1 are the same, of course.) There is also only one way to make the 5. The 6, on the other hand, can be made as 6 x 1 or 2 x 3.
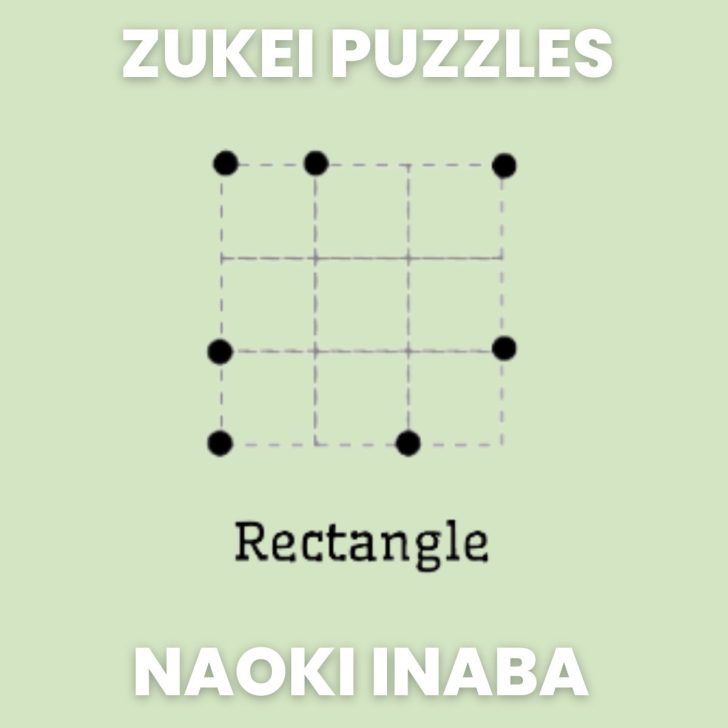
Zukei Puzzles
Inaba calls these a “Zukei” puzzle. Google Translate says the Japanese means “Looking for Graphic.”
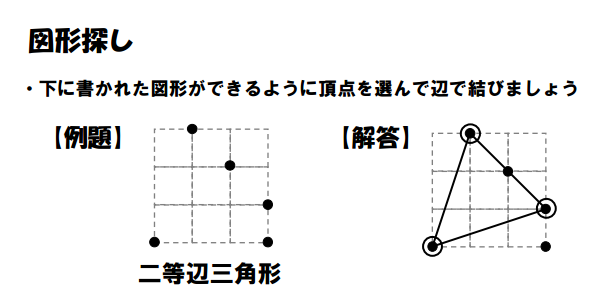
Unless you can read Japanese, this puzzle is probably much trickier than the previous puzzles to figure out. If you do Google Translate the text below the puzzle, you get “isosceles triangle.” Make sense now?
This is a PDF file of 42 puzzles for you to enjoy. Solutions are here. Because I’m nice and curious and hope to use this some day in the future if I ever teach geometry and I have a husband who is teaching geometry this year, I decided to go to the effort of translating each of the puzzle instructions.
These 42 puzzles cover the following geometry vocab words: square, rectangle, isosceles triangle, isosceles right triangle, right triangle, rhombus, trapezoid, and parallelogram. Here’s a Google Doc with the puzzle numbers and the corresponding shape that you are supposed to draw.
I think these puzzles are a must for any geometry class! It would even be fun to have kids make some puzzles with other vocabulary words as an extension!
Want to learn more about Zukei puzzles? I’ve written an entire post about them here.
Gemini Twin Puzzles
Inaba calls these “Gemini” puzzles. Google Translate Version: Gemini Formula. They are also known as “Twin Puzzles.”
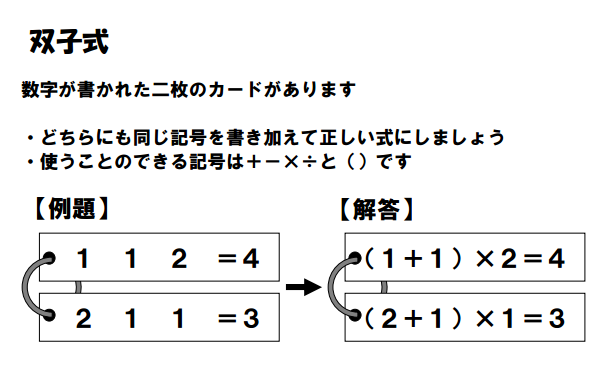
I was soooooooooo excited to run across these order of operation puzzles! You have to insert parentheses and operations so that both equations are true. And, to make things even trickier, you have to use the exact same parentheses and operations in BOTH equations!
Ready to do these with your students? You’ll find a PDF file of 42 of these puzzles here and solutions here. I’m definitely incorporating these into my review chapter for Algebra 1 this year!
UPDATE: Cathy Yenca has created a Desmos Activity Builder version of these Gemini Twin puzzles.
Dokoeq Puzzles
Inaba’s file name for these puzzles is “Dokoeq.” Google Translate changes the Japanese to “Where Kana Calculation.”
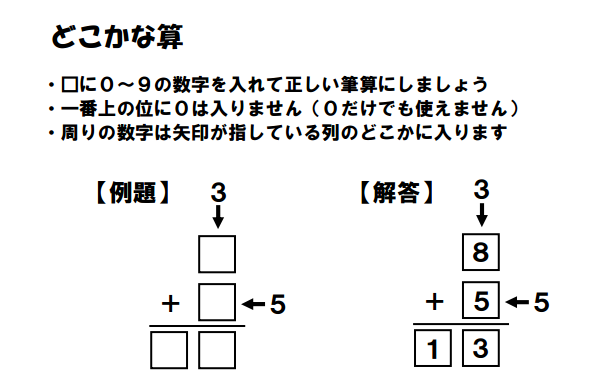
Image Source: http://inabapuzzle.com/study/dokoeq_q.pdf
These are much more elementary-looking puzzles, but I think they’d still make great warm-ups or brain-breaks in the secondary classroom.
The numbers and arrows tell you that there is a specific number in that row or column. In the case of the five, it’s clear what number MUST go in that box.
With the three, we know it can’t go in the top box because 3 + 5 does not equal a 2-digit number. Therefore, it must go in the bottom box.
There’s so much math and logic going on. I love it!
If you love them to, you’ll find 42 of these puzzles in this PDF file. Solutions are here.
Zero Puzzles
Inaba calls this puzzle “Zero.” Google Translate changes the Japanese to “Zero Zero Formula.”
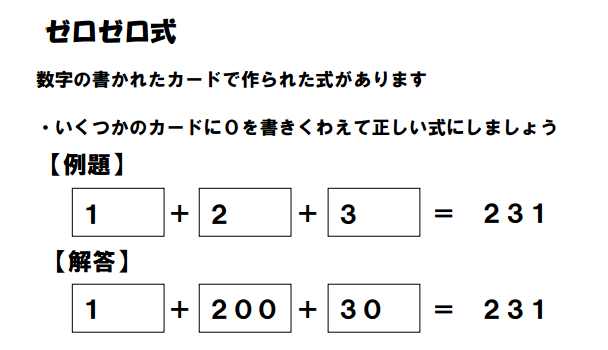
Do you see what I see? It’s a place value puzzle! You can only add zeros to each number in order to make them sum to the provided number.
This PDF file contains 49 of these puzzles and gets progressively harder. Solutions are here.
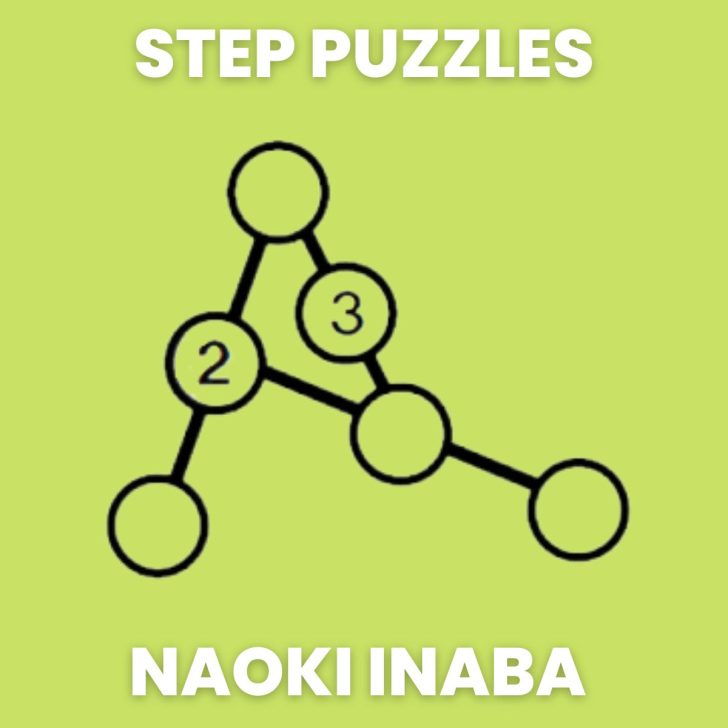
Step Puzzles
Inaba calls this a “Step” puzzle. Google Translate switches the Japanese to “Stairs of the Numbers.”
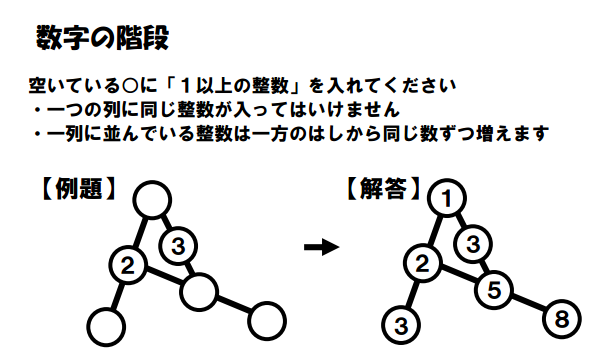
Each line represents a different arithmetic sequence. 1, 2, 3 is going up by 1. 1, 3, 5 is going up by 2.
And, 2, 5, 8 is going up by 3. The fact that they are overlapping just makes it even more fun. 🙂
This PDF file contains 42 of these puzzles with solutions posted here.
In Oklahoma, arithmetic sequences are now an Algebra 1 standard instead of an Algebra 2 standard. I’ll definitely use some of these puzzles as an intro into sequences.
UPDATE: I’ve written an entire blog post about Step Puzzles here.
More Printable Paper and Pencil Logic Puzzles
- Jobs that Use Mathematics Fill-In Puzzle
- Fall Fill-In Word Puzzle
- Product Square Puzzle
- Blank Sudoku Grid Printable
- Sixes Number Challenge
- 3-1-4 Pi Day Number Challenge
- Sankaku Puzzles
- Strimko Puzzles in the Classroom
- Square Sudokus
- Make It Pythagorean Puzzles
- Number Ball Puzzles by Naoki Inaba
- Hidato Puzzles
- Step Puzzles by Naoki Inaba – A Logic Puzzle for Introducing Arithmetic Sequences
- Kazu Sagashi Puzzles from Naoki Inaba
- Factor Tree Puzzles Inspired by Dr. Harold Reiter
- Strimko Logic Puzzles Review
- Tents and Trees Puzzles
- Slants Puzzles
- Angle Mazes by Naoki Inaba
- Zukei Puzzles
- Japanese Logic Puzzles for the Secondary Math Classroom
- Area Maze Puzzles from Naoki Inaba
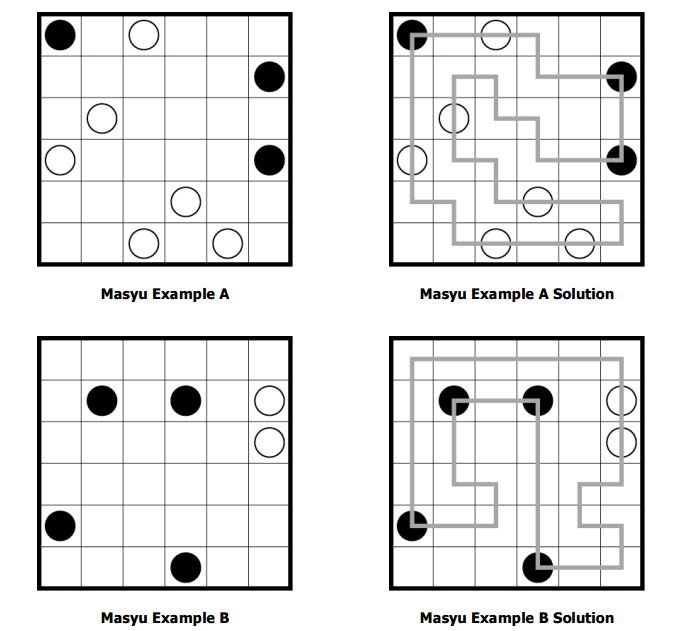
- Masyu Puzzles
- KenKen In The Classroom
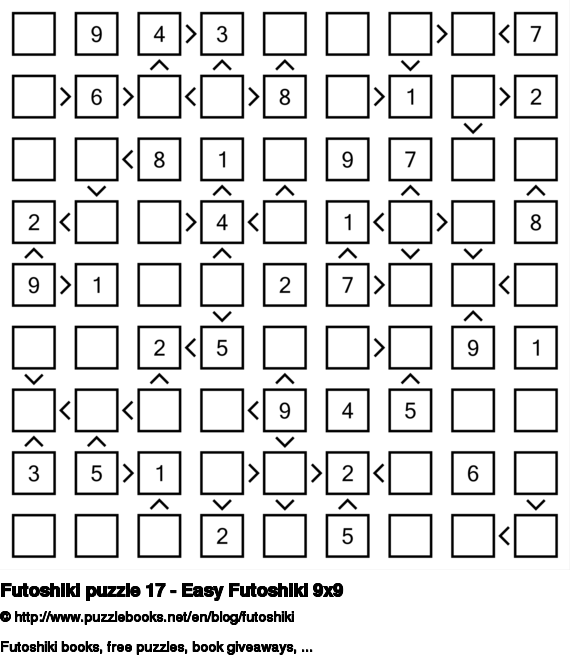
- Futoshiki Puzzles
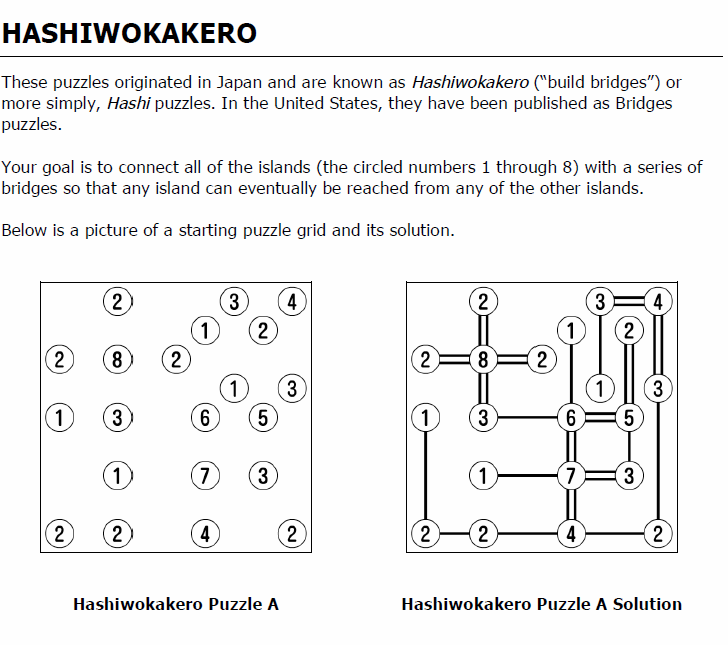
- Hashi Puzzles
- Shikaku Puzzles
- Nonogram Puzzles
- Digit Cells Puzzle
























I think I've got Puzzle 3: Kazu. Each puzzle that contains apples and oranges is asking a different question. For example, find the 2×2 (or 3×3) box containing more/less/the same number of apples and oranges. Using Google translate, it is easy enough to figure out if the question is asking for the same number or less. From what I can gather, Google is translating the word meaning "more" into the English word "cover." So questions 25-30 are asking for the 2×2 box containing:
25. same number of apples and oranges
26. more oranges than apples
27. fewer oranges than apples
28. more apples than oranges
29. fewer apples than oranges
30. same number of apples and oranges
Questions 31-36 are asking the same questions in the same order for the 3×3 box.
Questions 37-42 are asking for the difference in the number of apples and oranges in each box. So if the difference is 1, the box either contains one more apple than oranges or one less apple than oranges.
37. the difference in apples and oranges is 1
38. the difference is 2
39. the difference is 0
40. the difference is 1
41. the difference is 2
42. the difference is 0
Hope this helps!
– Julie
The name of the second one is "Triangle Search" and the third is "Count Search" (where "count" is a noun), from my moderate Japanese ability. It's actually the same word for "search" both times but it's written phonetically in the count search for some reason.
hmmmm
Are the Mizu puzzles meant to have only one solution? Are there any rules that narrow the ways to do it? I’m finding some different solutions and I don’t know if I am violating a rule. Thanks!
I believe there should only be one solution to the mizu puzzles. I found some of them to be quite tricky when I worked them out several years ago.