Step Puzzles by Naoki Inaba – A Logic Puzzle for Introducing Arithmetic Sequences
The last time I taught Algebra 1, I used Step Puzzles by Naoki Inaba to introduce the idea of arithmetic sequences. I tweeted about it, but in the craziness of packing up my classroom and house to move last summer they never made it up on my blog.
I was first introduced to the amazing logic puzzles of Naoki Inaba in 2016 when I discovered his area maze puzzles which have become quite popular.
On his website (which is entirely in Japanese…), Inaba shares a collection of logic puzzles that are PERFECT for the math classroom. I ended up creating an entire page on my blog dedicated to Inaba’s puzzles.

Since then, I’ve slowly been in the process of translating these puzzles and putting them into a more user friendly format for use in the classroom. So far, I’ve blogged about Angle Mazes, Zukei Puzzles, and Kazu Sagashi Puzzles.
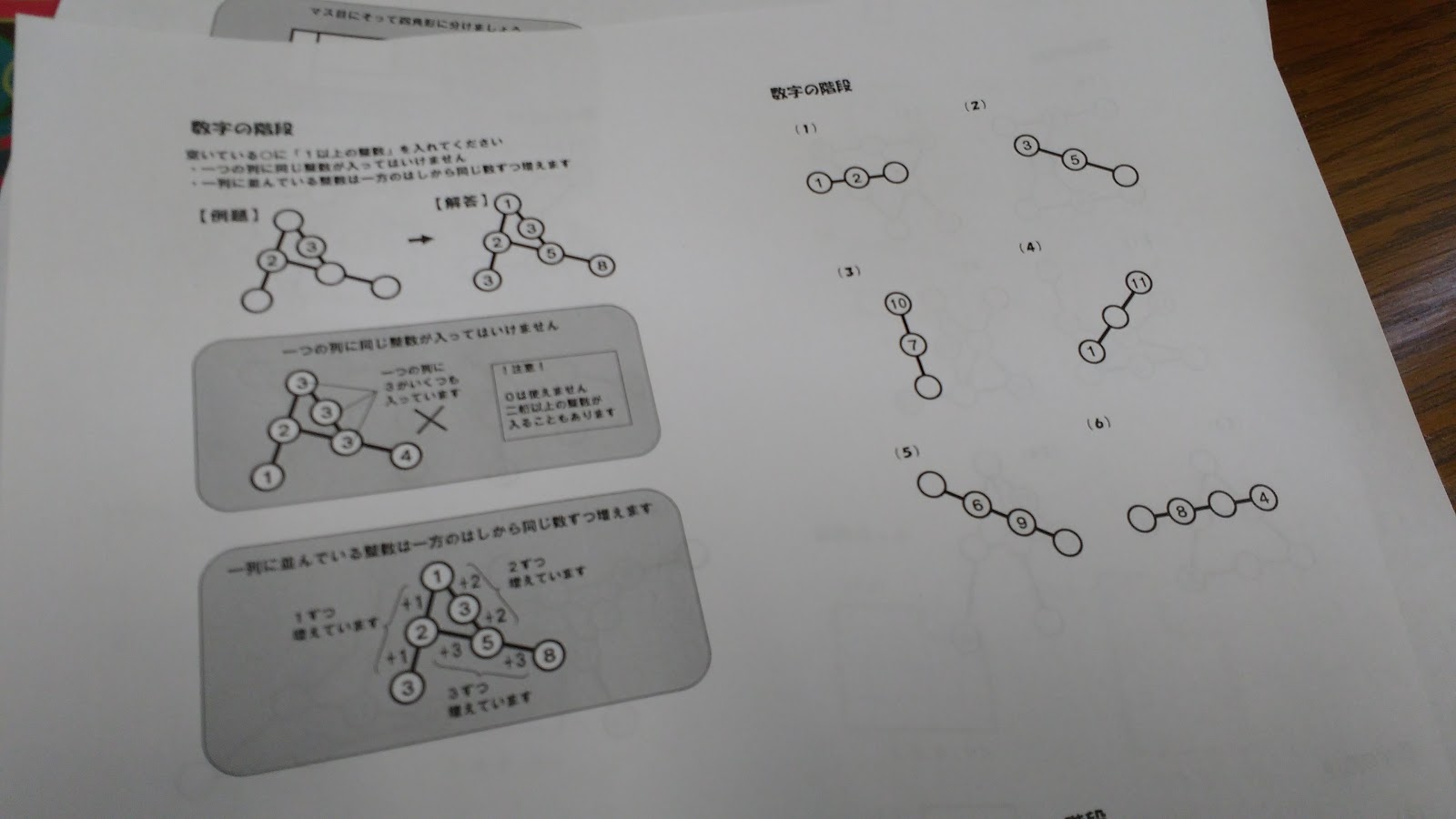
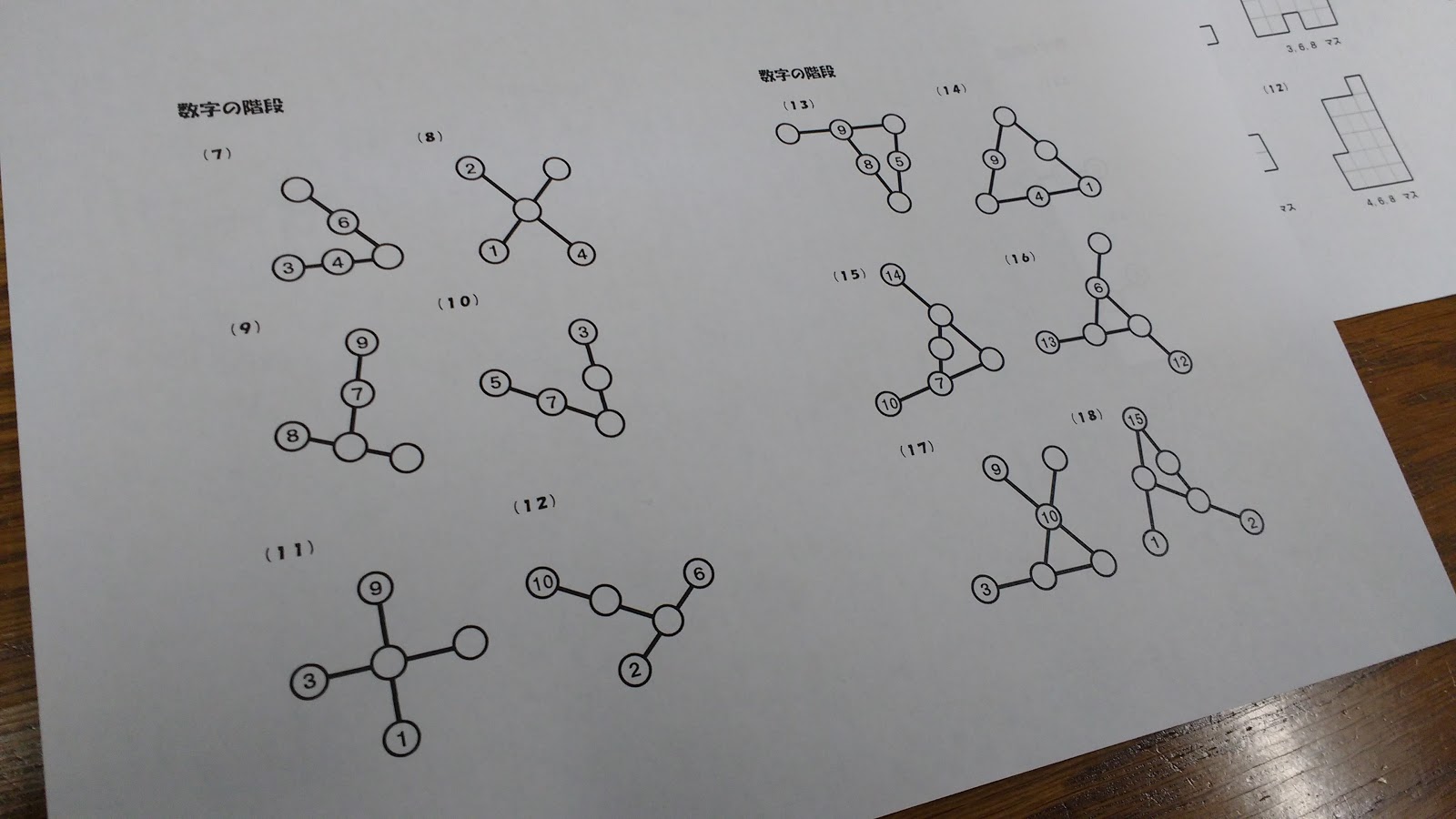
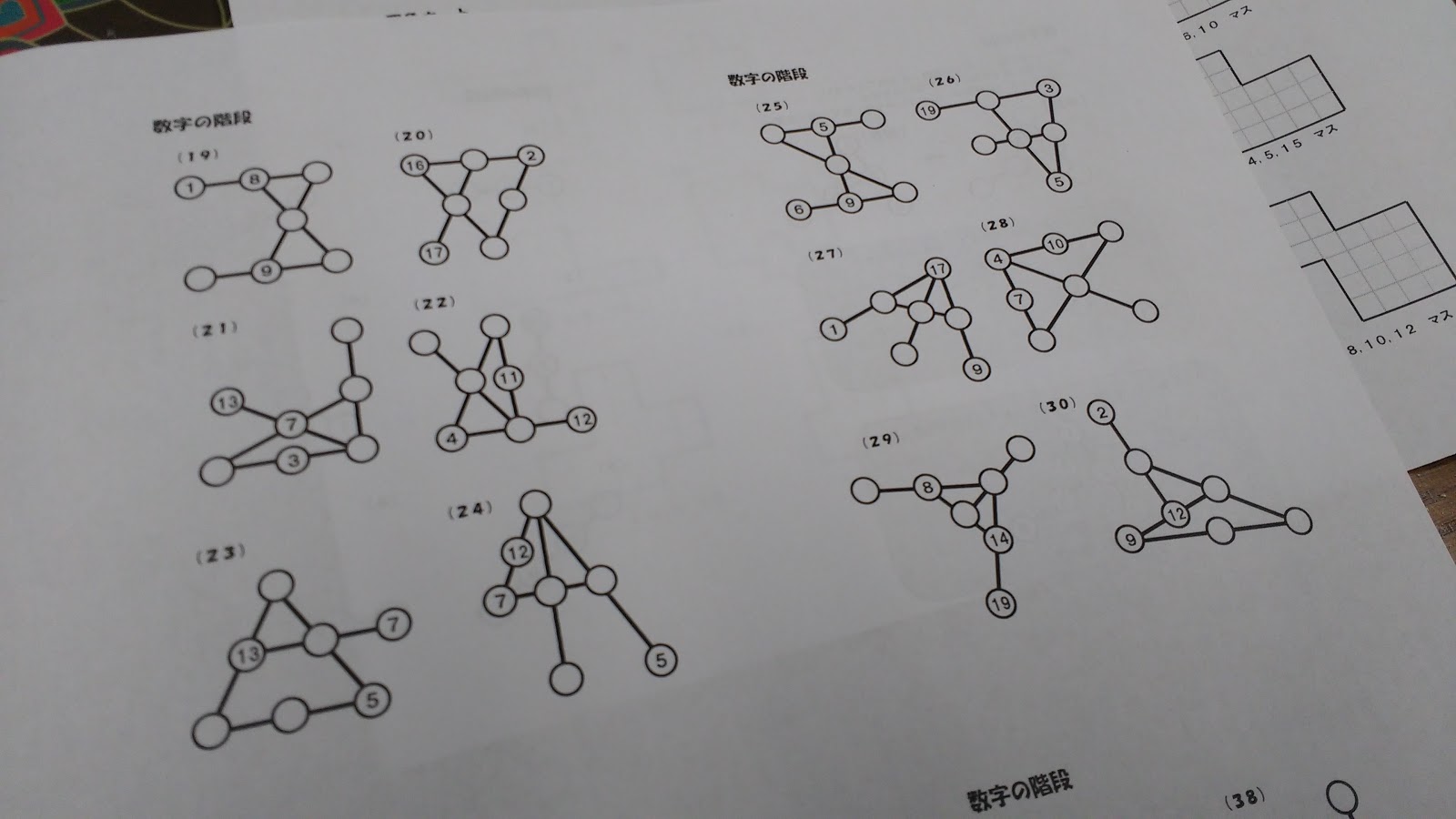
At the beginning of this month, Simon Gregg tweeted me to ask if I had reformatted Inaba’s Step Puzzles to fit more to a page than the original PDF. I had, and this tweet reminded me that I was over a year late in blogging about this!
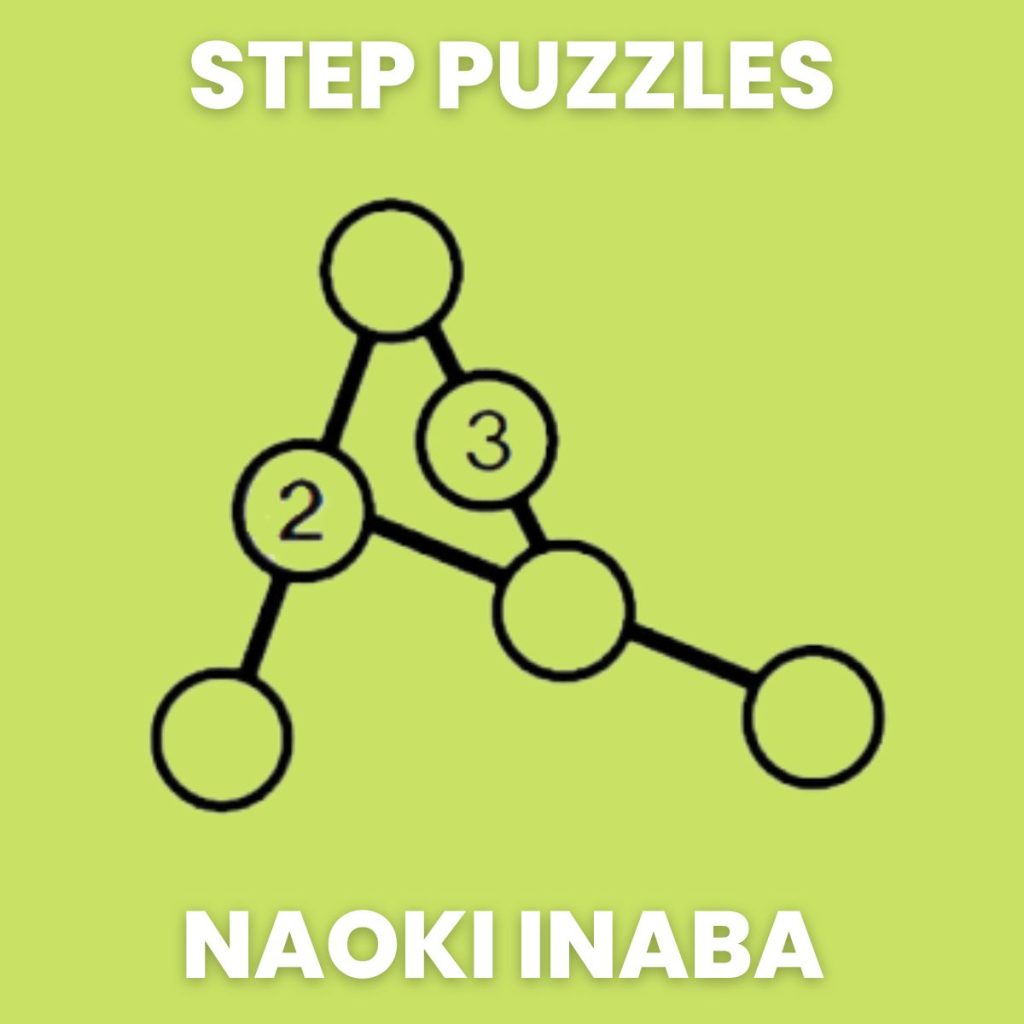
I like to introduce step puzzles to students by showing them a puzzle and its solution and asking them to figure out the rules of the puzzle.
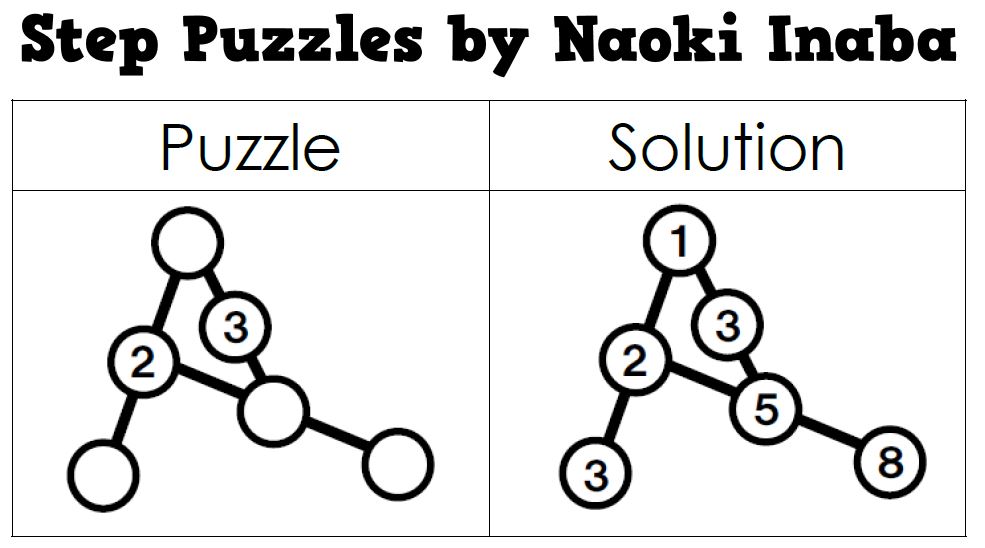
Because of this problem-solving based introduction to step puzzles, I have not typed out the instructions on the puzzle sheet that I give to students. I have another reason for this. These puzzles are accessible for students as young as elementary school. They are still engaging for middle school and high school students. But, with these age groups, students can be instructed to place numbers in each circle so that each line forms an “arithmetic sequence.” This proper vocabulary would likely intimidate an elementary student who could easily tackle these puzzles with an age appropriate introduction.
The puzzles start out quite simply.
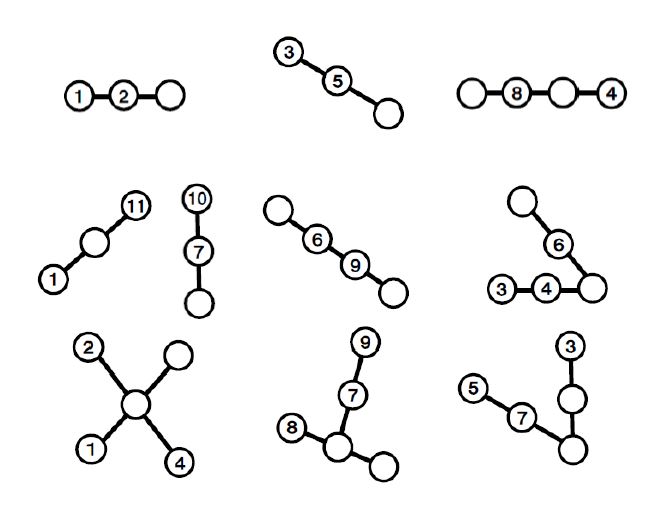
Sometimes my students have used the first puzzle to make an incorrect assumption about how the puzzles work. They assume that 1, 2, 3 is the answer to the first puzzle because 1 + 2 = 3. When really, it is 1, 2, 3 because 1 + 1 = 2 and 2 + 1 = 3. You can check student understanding of this by having them solve the second step puzzle 3, 5, ___. The correct answer is 7. Students with the prior misunderstanding would answer 8.
I’ve found that once I set students straight from this misunderstanding that they seem to be good to start tackling the puzzles on their own.
The puzzles quickly progress in difficulty. Soon students have to start figuring out where to start solving the puzzle. If students start in the wrong place, the puzzle will seem impossible.
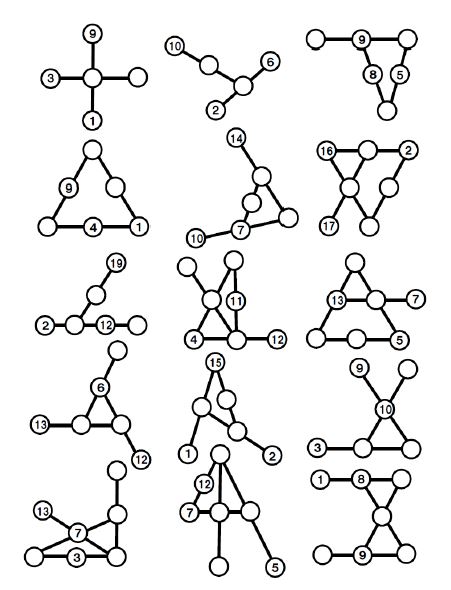
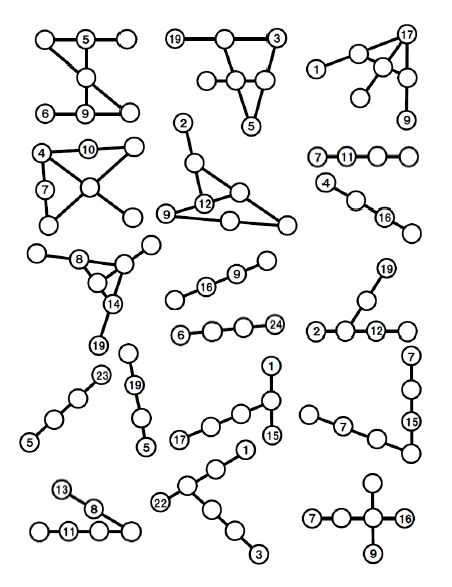
Before I close out this blog post, check out how Simon Gregg combined WODB (Which One Doesn’t Belong) with Step Puzzles!
Free Download of Step Puzzles by Naoki Inaba
You can download Inaba’s original Japanese version of these puzzles here.
Here are my space-saving versions I created for classroom use.
Click here to Download
Step Puzzles by Naoki Inaba (PDF)
4405 downloads – 275.42 KB
Puzzle Solutions
Puzzle solutions are available on a password-protected solution page. I do not openly post the puzzle answer keys because one of my goals as a resource creator is to craft learning experiences for students that are non-google-able. I want teachers to be able to use these puzzles in their classrooms without the solutions being found easily on the Internet.
Please email me at sarah@mathequalslove.net for the password to the answer key database featuring all of my printable puzzles and math worksheets. I frequently have students emailing me for the answer key, so please specify in your email what school you teach at and what subjects you teach. If you do not provide these details, I will not be able to send you the password.
Not a teacher? Go ahead and send me an email as well. Just let me know what you are using the puzzles for. I am continually in awe of how many people are using these puzzles with scouting groups, with senior adults battling dementia, or as fun activities in their workplace. Just give me enough details so I know you are not a student looking for answers to the puzzle that was assigned as their homework!



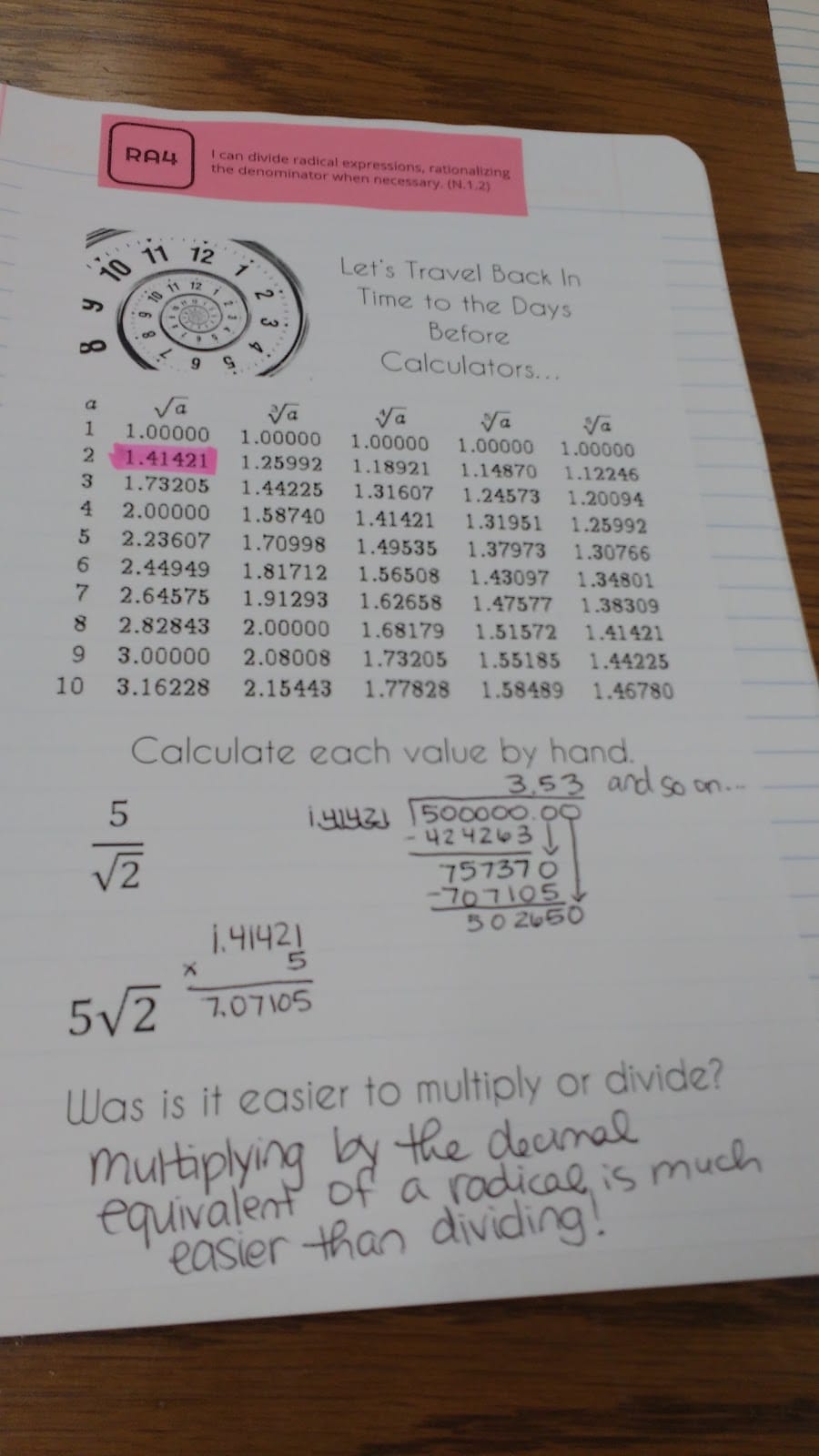




This is great, but could you share your answer keys? Also, how do you help students know where to start. I love your blog! Thanks for such great ideas.
Naoki Inaba has an answer key for this puzzle on his website!