This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.
Want to check out my favorite Amazon items for the classroom? Check out my Amazon favorites page!
This week, I’m trying out the Arrows Puzzle which is a different sort of puzzle on the puzzle table. Instead of being a puzzle where students have to arrange various laminated pieces like I frequently use, this is a coloring puzzle.
To make things easier on students, I placed the puzzle inside an 11 x 17 dry erase pocket.
MATH = LOVE RECOMMENDS…
I cannot imagine teaching math without my dry erase pockets! They instantly make any activity more engaging and save me countless hours at the copy machine since I can use the same class sets of copies year after year.
Here are my current go-to recommendations:
If you are looking to save a bit of money, you can also pick up a package of 11 x 17 sheet protectors for a much cheaper price! They won’t be quite as durable, but students can still write and erase with their dry erase markers.
This puzzle, written by Erich Friedman, is featured in Puzzle Box, Volume 1 by Dover Publications.
My students have seemed a bit intimidated by this puzzle this week, so I’m wondering if I need to rewrite the instructions somehow. The goal of the puzzle is to color a subset of the given arrows so that each uncolored arrow points at exactly one other uncolored arrow and each colored arrow points at exactly two other colored arrows.
Some of my students who are regulars at the puzzle table read the instructions and immediately decided this puzzle was not for them without even attempting it. I’m wondering if the coloring aspect is part of the issue. If I laminated and cut out different colored/uncolored arrows that students could place on the puzzle board, would they be more willing to give the puzzle a try?
During my planning period today, I sat down with a student who often hangs out in my room during my planning period (he has a free hour), and solved this puzzle with him. Once I read the instructions and re-explained what it meant for an arrow to point at other arrows, he was able to pretty much solve the puzzle with only a tiny bit of guidance from me.
This makes me think that this puzzle would make a better class-wide challenge than a puzzle table challenge which is more of a tackle-it-on-your-own-if-you-are-so-inclined challenge.
Digital Version of Arrows Puzzle
Kathy Henderson has created a digital version of this Arrows Puzzle in Desmos Activity Builder.
Free Download of Arrows Puzzle from Erich Friedman
Arrows Puzzle (PDF) (1585 downloads )
Arrows Puzzle (Editable Publisher File ZIP) (819 downloads )
The arrows puzzle is designed to print on 11 x 17 cardstock, but you can easily print it scaled to ~65% to print it on letter sized paper.
Interested in more puzzles for your classroom? Check out my blog page dedicated to all things puzzles.
Puzzle Solutions
I intentionally do not make answers to the printable math puzzles I share on my blog available online because I strive to provide learning experiences for my students that are non-google-able. I would like other teachers to be able to use these puzzles in their classrooms as well without the solutions being easily found on the Internet.
However, I do recognize that us teachers are busy people and sometimes need to quickly reference an answer key to see if a student has solved a puzzle correctly or to see if they have interpreted the instructions properly.
If you are a teacher who is using these puzzles in your classroom, please send me an email at sarah@mathequalslove.net with information about what you teach and where you teach. I will be happy to forward an answer key to you.
More Dry Erase Puzzles
- Eights Challenge
- Lines of 3 Puzzle
- Equal Sums Puzzle
- Sevens Number Challenge
- Sixes Number Challenge
- Fives Challenge Puzzle
- 3-1-4 Pi Day Number Challenge
- Fours Challenge Puzzle
- Threes Challenge
- Twos Challenge
- 9 Pumpkins Puzzle
- Connect the Shapes Puzzles
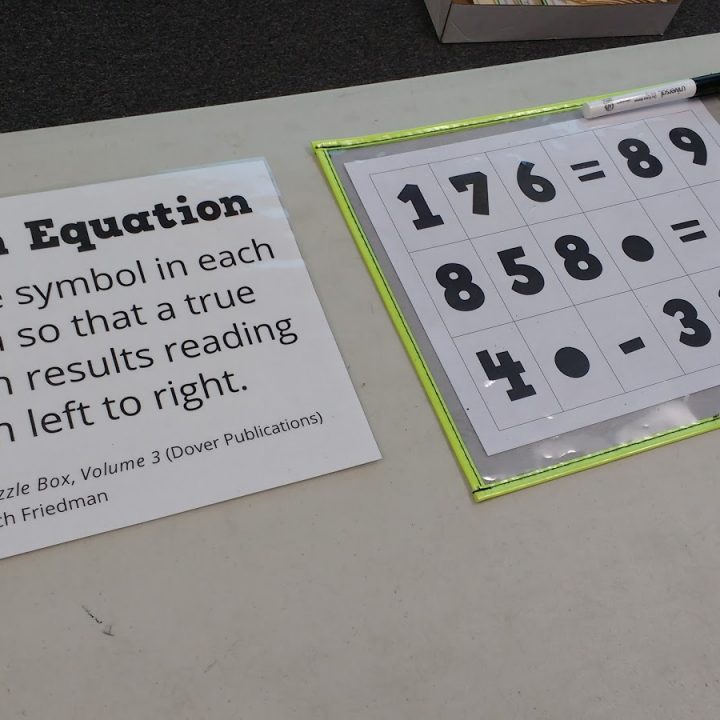
- Hidden Equation Puzzle 3
- X Marks the Spot Puzzle
- Hidden Equation Puzzle 2
- Shape Grid Puzzle
- 145 Doors Puzzle
- Tic Tac Total Puzzle
- Connect the Dots Puzzle
- Hidden Equation Puzzle 1
- Arrows Puzzle
- Maximize the Sum Puzzle
- 9 Dots Puzzle
- How Far Can YOU Climb? – An Activity by Frank Tapson
Connie
Friday 9th of March 2018
An example of what "points at exactly two other colored arrows" and "points at one other uncolored arrow," whether or not they turn out to be correct, might clarify the directions. Right now, you're left wondering how an arrow points at two arrows. Perhaps the solution is to start together as a class, get partway, and let those who are inclined finish.
Please clarify the directions for us so we can attempt the puzzle.
Carla R
Wednesday 25th of April 2018
This comment has been removed by the author.
Carla R
Wednesday 25th of April 2018
I was able to solve it by assuming that when it says "points directly at" it means that in its line of sight, a coloured arrow must have two coloured arrows in that direction. So you can skip an arrow, but in the direction it is pointing, a coloured arrow would point towards two coloured arrows. An uncoloured arrow would have one uncoloured arrow in its direction. Not sure that makes sense but it worked for me that way.
Adina
Friday 9th of March 2018
Maybe the directions do need to be reworded. I know my students would be scared off by the word "subset." Also, how does an arrow point to more than one other arrow?