Probability Bingo Game

One of my favorite statistics activities for introducing probability is Probability Bingo. Probability Bingo is not your typical bingo game. You aren’t looking for five in a row. Instead, the winner is the first person to fill up their ENTIRE bingo card.

I once attended an AP Summer Institute for AP Statistics at the University of Tulsa with Dave Ferris. Dave is an AP Stats teacher in Noblesville, IN.  He has a website that is chock full of stats resources.

On Dave’s probability resource page, I found a file called “Probability Bingo.”  I opened the file, and I was instantly intrigued.  (By the way, the file gives credit to Brian Mehmed, 2011 WV APSI.)  

Here are the instructions at the top of the bingo card:

Each of two die has colored faces, 3 green, 2 blue and 1 red. The two dice will be rolled. The outcome will be considered to be one “bingo call.” If you have this outcome on your bingo card, mark it off.

The winner will be the student who gets a bingo card completely marked off (all 25 squares). Mark each square on your bingo card (use BG for “blue green,” BB for “blue blue,” etc.) so that you have the best chance of winning.

I used one inch wooden cubes and dot stickers to create a set of probability bingo dice for my classroom.

I used Mod Podge to seal down the colored stickers so students could not peel them off the dice.

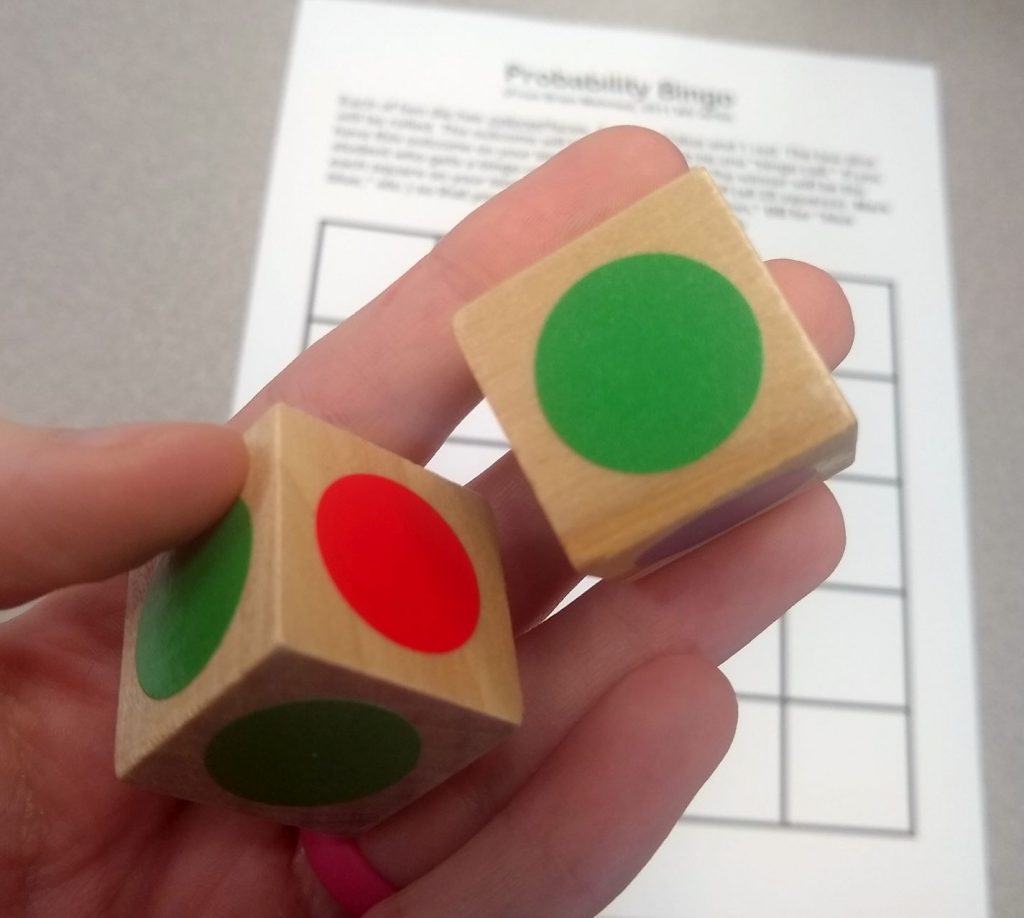
Before I got fancy, I used to use the small blank foam cubes that you can buy at Dollar Tree to create custom dice. I would write the letter for each color on a side of the cube using a Sharpie.

I have also taken post-it notes and taped them to the sides of a large foam die. Some years I have even had students create the dice themselves!

To prep for this activity, you will need to make the colored dice described in the instructions and print a set of probability bingo cards for the class. I print the bingo cards double-sided because students ALWAYS want to play a second round!

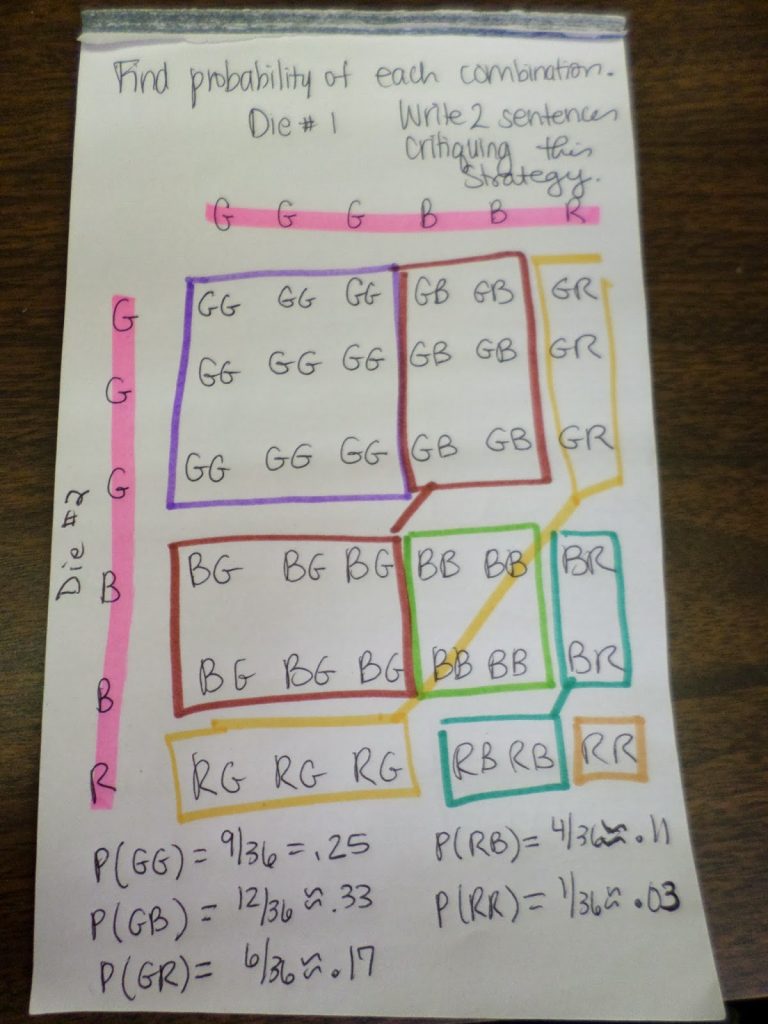
I discuss how the dice were made, and students get to work filling out their bingo cards. The first time I ever did this with students, I decided I wanted to play along. I quickly calculated the probability of each combination of colors.  

I multiplied each probability by the 25 bingo squares to determine how many squares I should label with each color.  I had one square left at the end, so I went ahead and labeled it RR even though the probability of rolling a RR is approximately 0.03.

The students took turns rolling the two dice.  With each roll, we marked off the combination once.  This is not your typical bingo game.  You’re not looking for five in a row.  You’re looking to be the first to fill up your entire bingo card.  

At first, I was off to a good start.  With every roll, I got to mark off a square.

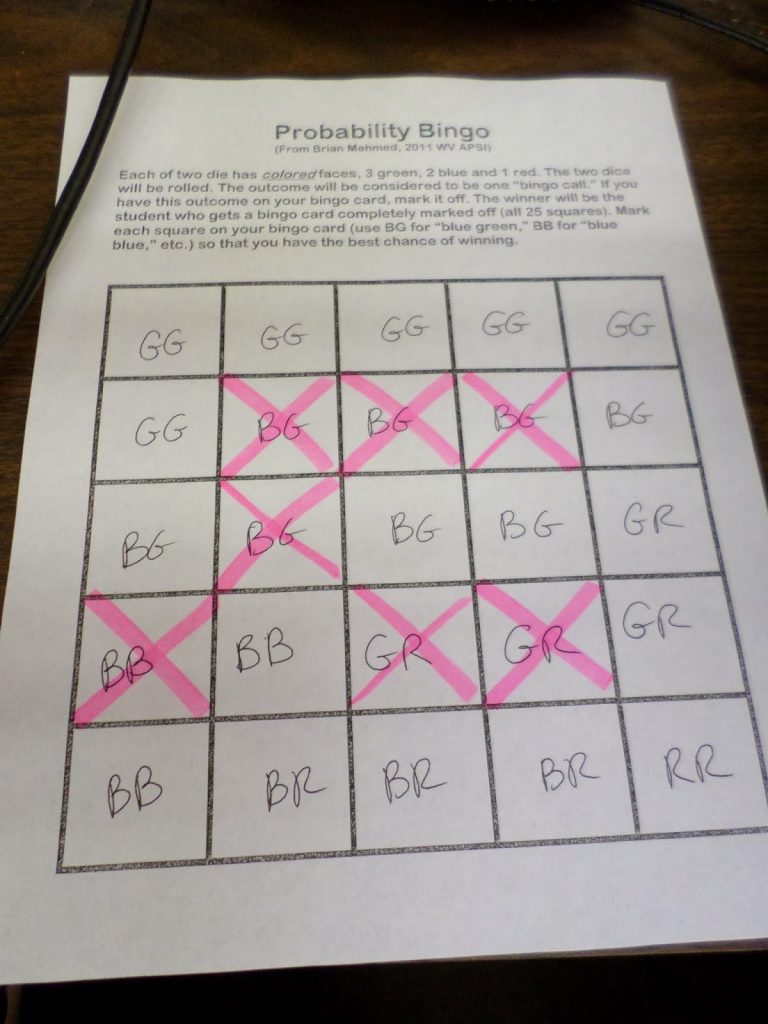
Then, the dark time began.  I quickly ran out of Blue/Green squares.  So, did my students.  We all agreed that we should have put more Blue/Green squares on our probability bingo cards.  The GG combination was not rolled as much as I would have liked.

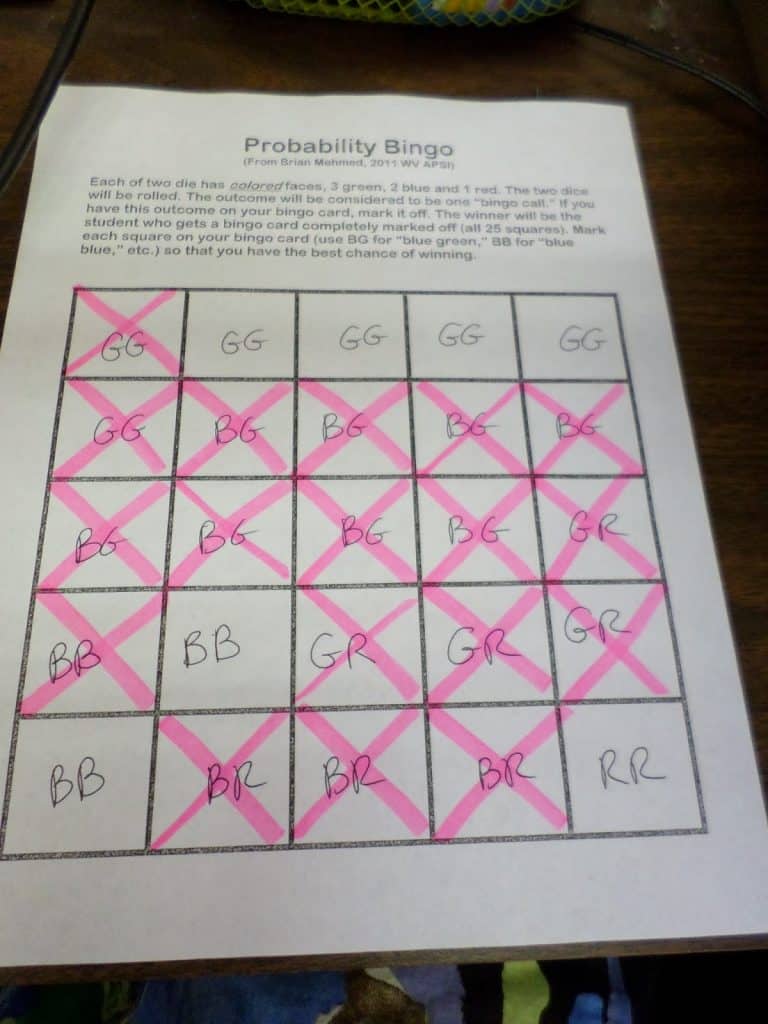
I didn’t take a picture of it, but I sat for a long time with only my RR square unmarked.  I wasn’t the only person waiting for an RR.  Eventually, an RR was rolled, and I won!

My students instantly wanted to play again.  I had anticipated this, hence the double-sided bingo cards.  Based on our first round of bingo, my students set out to create a better bingo card.  

One of my students decided to calculate the probability like I had.  She accidentally left the BB combination off of her card.  She was not happy about this!

Just for fun, I decided to leave my card exactly the same since I had won the first round.

Here’s the start of Round 2 of Probability Bingo.

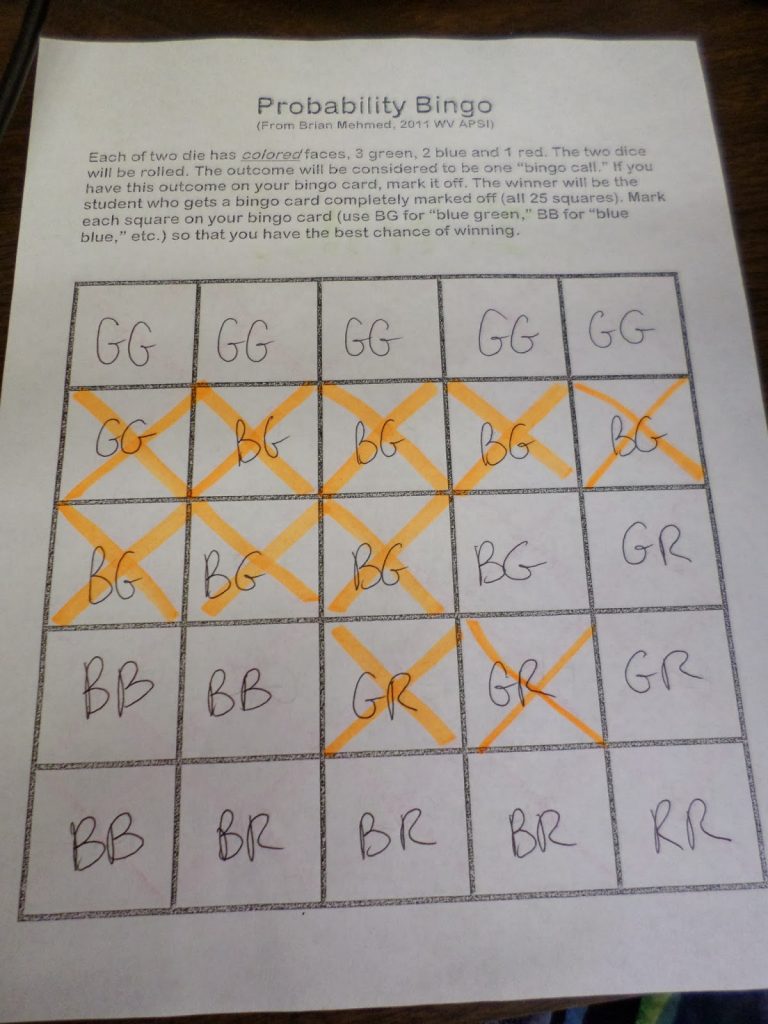
Pretty soon, history repeated itself.  Once again, I found myself waiting and waiting and waiting for RR.

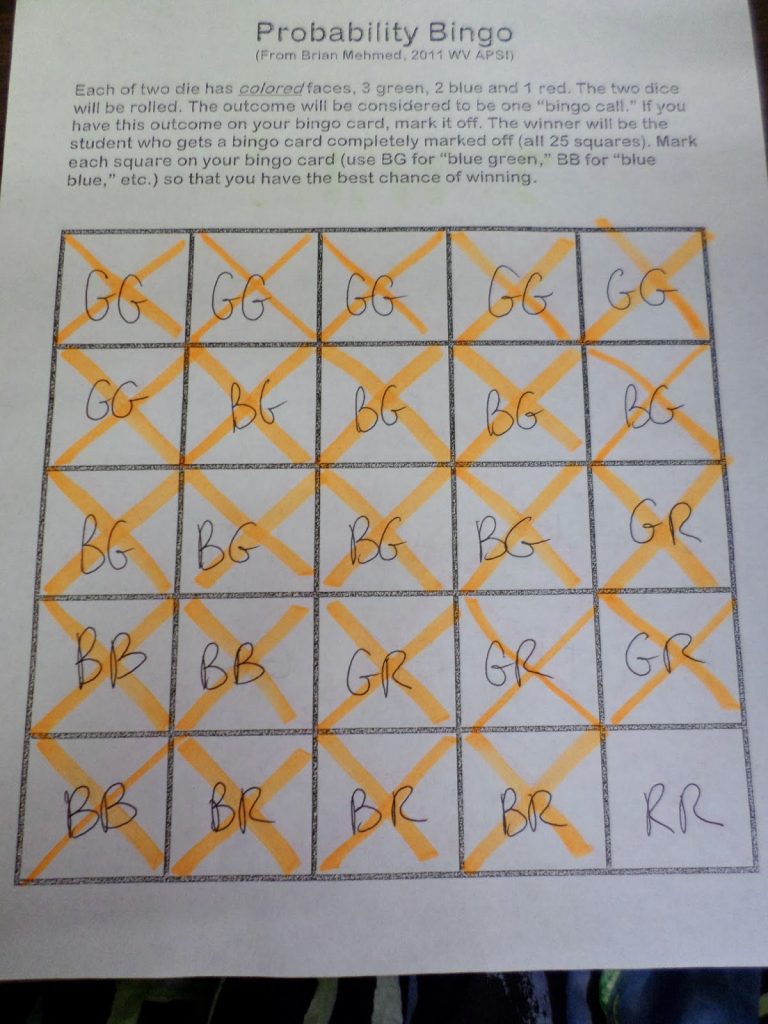
That Red/Red combination never came because another student filled up her card first.  The moral of the story?  If there’s only a 3% chance that something will be rolled, don’t put it on your bingo card.

In order to give my students a grade for the day, I asked them to calculate the probability of rolling each color combination.  Then, they had to critique the strategy of designing your card to reflect these probabilities.

I would definitely recommend this probability bingo activity!  It was thought-provoking and fun.  If time allows, I would love to play this with my Algebra 1 students when we review probability at the end of the year.

Link to Download Probability Bingo

http://noblestatman.com/AP_Stats_Workshops/Probability_files/Probability%20Bingo.doc