End Behavior of Rational Functions Stations Activity

Practice identifying the end behavior of rational functions using these six fun and engaging stations activites that are designed for AP Precalculus (1.7).

This is my first year teaching AP Precalculus, and it has definitely been an adventure so far. I have to admit that I have never actually taught my precalculus students to describe the end behavior of rational functions using limit notation before. So this year has been a learning experience for all of us!

At my school, I actually only see my students in class four days a week. On Mondays, students complete an asynchronous assignment at home. The only students in the building on these “Distance Learning Mondays” are students who are failing one or more courses and any students who want to come in for extra help or to make up missing assignments.

My AP Precalculus students ended up watching a video over the end behavior of rational functions and completing a worksheet as their asynchronous assignment, so I decided to create a set of stations for students to work through on the following day in class to help me gauge how well they had understood the previous day’s lesson.

I ended up creating five end behavior of rational functions stations for students to work through: two truths and a lie, matching graphs and equations, creating rational functions to meet various criteria, complete the limit statements, and building rational functions (my personal favorite!).

Two Truths and a Lie with Rational Functions

I created two different sets of 2 truths and a lie statements for students to work through. Each set features three statements involving the end behavior of rational functions.

Two of the statements are true. One is false. Students must identify which statement is the lie and explain why.

Set A focused on student understanding of identifying which type of asymptote each rational function has given an equation. It tested student knowledge of the phrases “slant asymptote” and “horizontal asymptote” as well as their understanding of limit notation.

I intentionally made the equation for f(x) look like it might have a slant asymptote at first glance.

Set B was a bit more difficult because it involved looking at four different rational functions.

I printed these two truths and a lie templates and slid them in dry erase pockets so students could write directly on them.

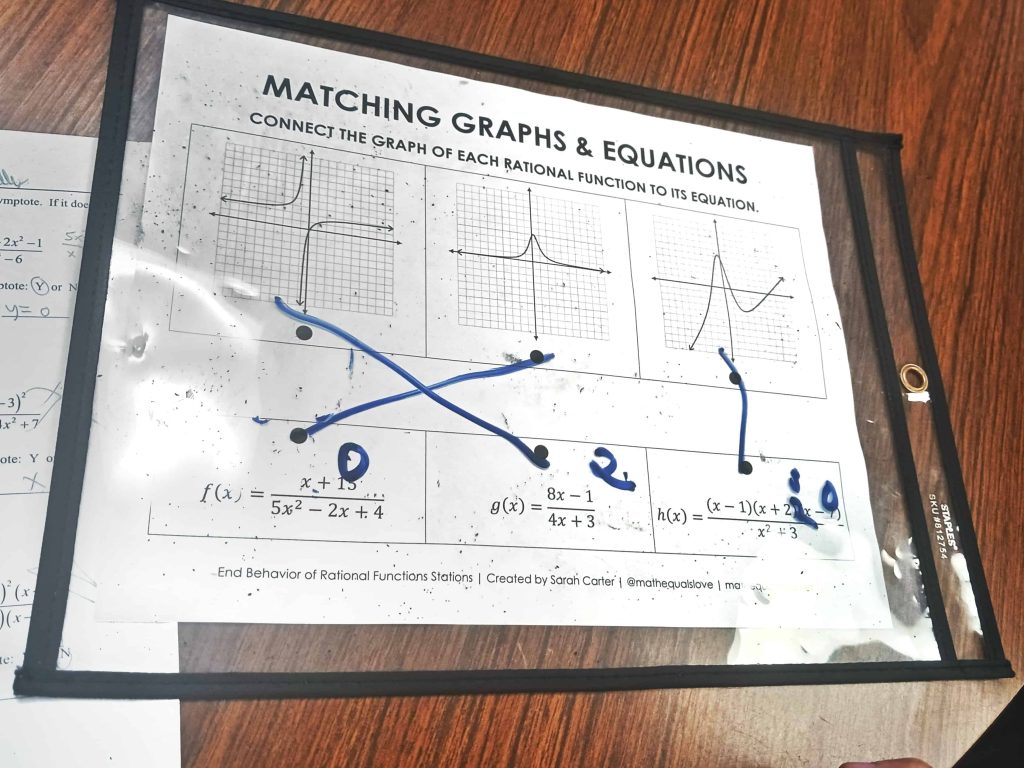
Matching Graphs of Rational Functions and Equations

This matching activity features the graphs of three rational functions and their equations. Students were to draw a line connecting the graph to its equation.

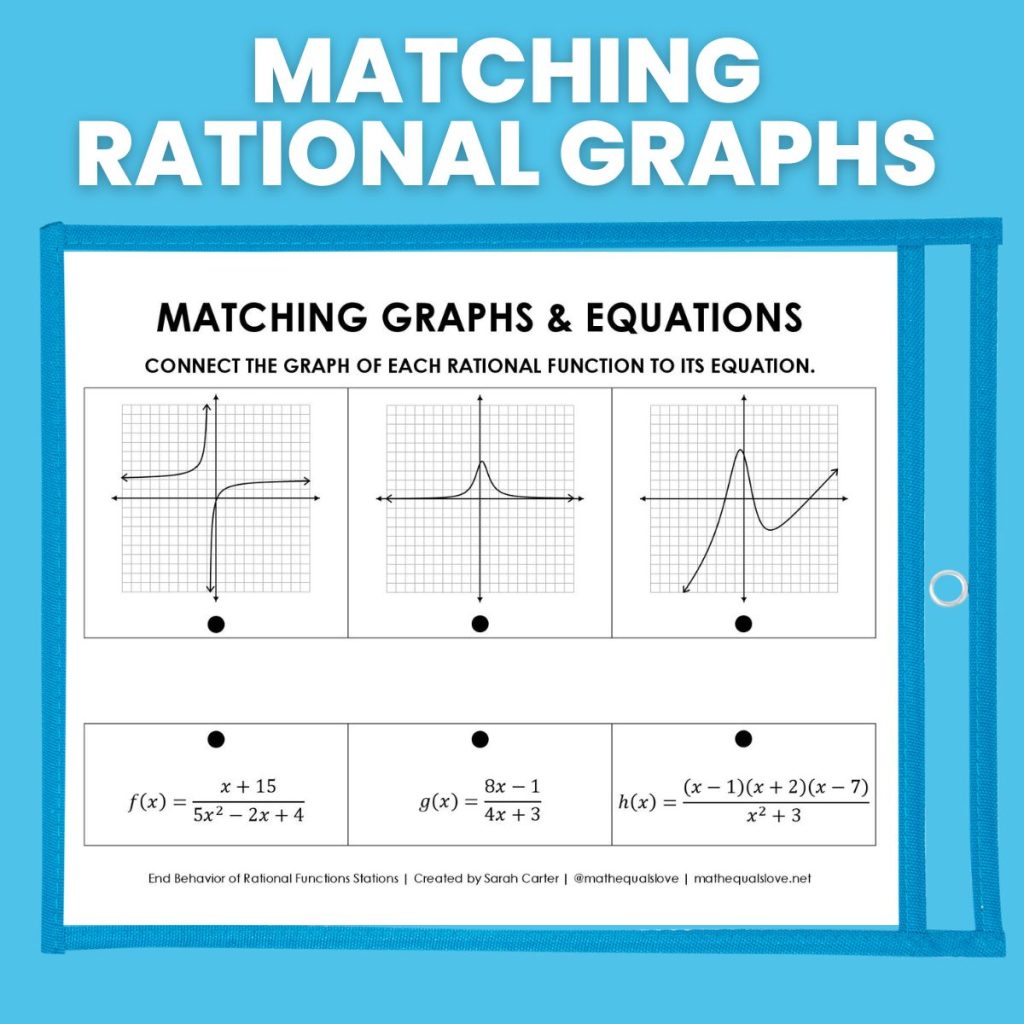
By far, this was the easiest station for students to work through. Each of the functions had a different end behavior, so students could easily match the graphs and equations once they found the end behavior of each equation.

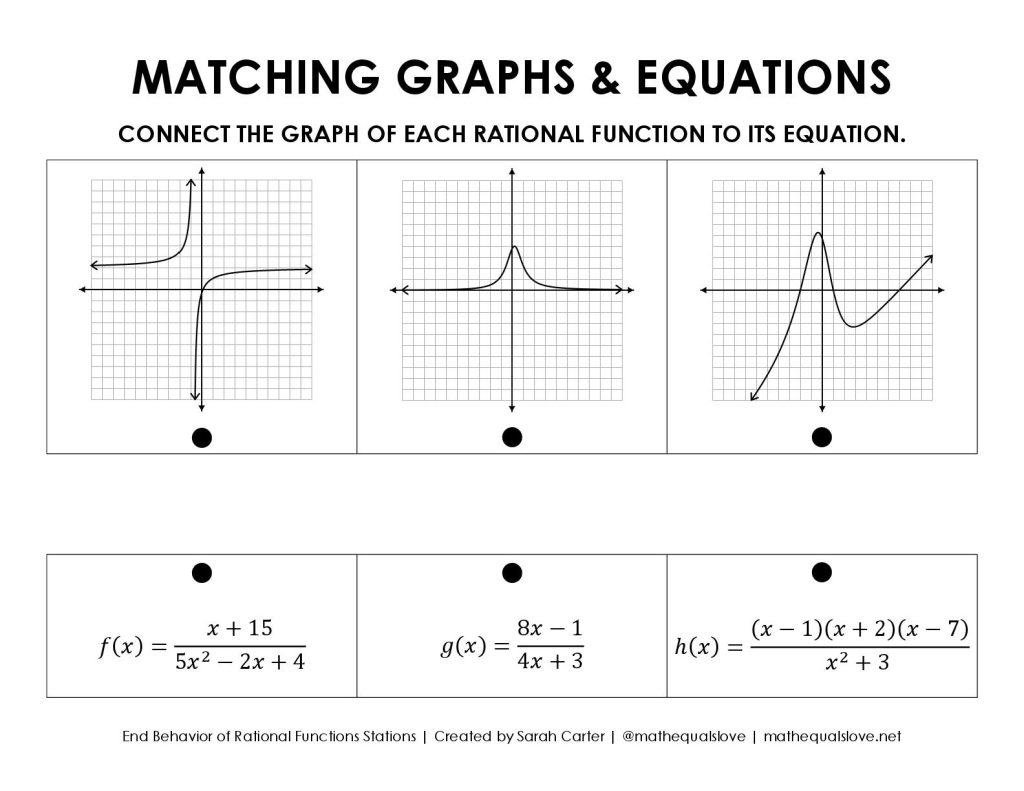
I also used dry erase pockets with this station so students could draw on top of the sleeves with dry erase markers.

Creating Rational Functions Activity

To step up the difficulty a bit, I created a station where students were given four statements and had to create a rational function that met each description.

It was interesting to watch my students work through this station. Almost every group of students left h(x) for last.

The only downside to this station was that it was a tiny bit more time consuming to check student work than the other stations since answers could vary.

Complete the Limits Statements Activity

I originally wanted to make a matching activity with equations and limit notation, but I could figure out how to make it work with each function needing a different letter name.

I ended up getting around this by changing it from matching to “complete the limit statements.”

Determine which function must be written in the blanks of each pair of limit statements to create true statements regarding the end behavior.

I also printed this one and slid it in a dry erase pocket for students to be able to write on, but I guess I didn’t get a picture of this one in action.

Building Rational Functions Activity

My favorite station was this building rational functions activity. It was also the most difficult station.

Students were given four different pairs of limit statements describing the end behavior of four different rational functions. Then, they were given eight expression pieces that I printed on Astrobrights colored paper, laminated, and cut apart.

Students had to arrange the expression pieces as numerators and denominators in the spaces provided on the template to build functions with the given end behaviors. Each piece may only be used once.

It was very interesting watching students logic through this puzzle. Almost every group figured out that the horizontal asymptote of y=4 on g(x) greatly narrowed down the possible puzzle pieces to form g(x).

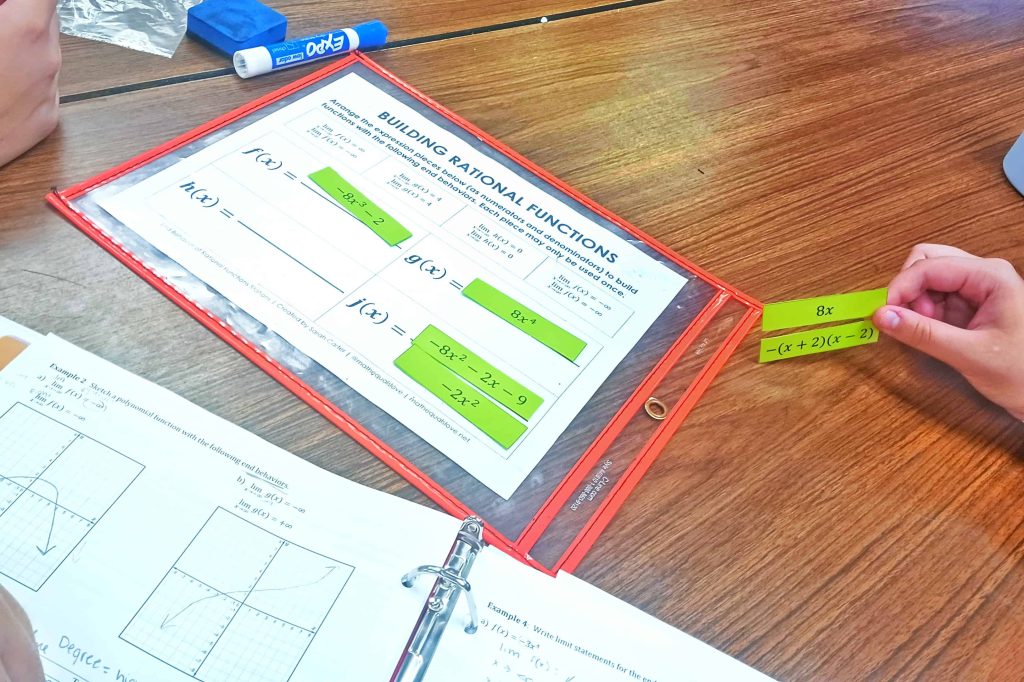
They struggled quite a bit more determining where the function pieces had to go for f(x), h(x), and j(x).

This station had the least number of students complete it correctly out of all the stations.

I still think this is the best station out of this set. If had to choose just one of these stations to use as a stand-alone activity instead of a set of stations, this would be the one I chose.

Ideas for Implementing these Stations in Class

I only had about 25 minutes of a 50 minute class period to dedicate to these stations, so I didn’t implement them the way most people probably would have.

If I was using a longer period of time on these stations, I would have students complete the stations in the following order:

1. Matching Graphs and Equations
2. Two Truths and a Lie
3. Creating a Rational Function
4. Complete the Limit Statements
5. Building Rational Functions

Since I had limited time, I decided to classify each station as MILD, MEDIUM, or SPICY. I gave each pair of students the choice of which level to start with.

MILD: Matching Graphs and Equations

MEDIUM: Two Truths and a Lie, Creating Rational Functions, Complete the Limit Statements

SPICY: Building Rational Functions

Most pairs of students chose to start with mild or medium. But a few students chose to jump straight to spicy.

I think they would have been more successful at the building rational functions challenge if they had done a few of the medium level stations first.

So if I were to do this again, I would only give students the choice between mild and medium to start with. After a group had solved at least two medium stations correctly, I would then ask them if they wanted to try the spicy challenge.

I am definitely open to hearing suggestions for running stations in the classroom. Even though this is my 12th year of teaching, I can probably count on my hands the number of times I have done stations activities with students.