Graphing Inequalities Foldable

This graphing inequalities foldable was inspired by a foldable I saw on Coffee Cups and Lesson Plans.  

I started this unit by drawing the different inequality symbols on my Smart Board.  I wrote numbers above each symbol.  Then, I asked a simple question, “Who can tell me which number is above the symbol that means less than?”  

Hands shot up in the air.  Some students gave me the correct number.  Others had confused the symbol for less than with the symbol for greater than.  Still others had confused it for the less than or equal to symbol.  

One student argued that there was no way of knowing because there were no numbers for the alligator to eat. 

Graphing Inequalities Foldable

Oh, the alligator.  I remember learning about the alligator in elementary school.  

The alligator is a really hungry animal.  He always chooses to eat the largest number of fish possible.  I even did a project for my ed psych class in college where I taught a kindergartner about inequality symbols using the alligator.  

Now that I’m teaching algebra, I can’t stand the alligator.  The alligator doesn’t help my students translate symbols into words.  The alligator holds my students back.  So, I told them that they had to take everything they ever learned about the alligator and throw it out the window.  

I thought there was going to be a revolt in my classroom.  One student proclaimed, “That’s half of my life!  You can’t expect me to just throw away half of my life because you don’t like the alligator.”

When I look at an inequality symbol, I just know its name.  I guess I just memorized them somewhere along the way without realizing it.  

Last year, one of my college algebra students was having a terrible time remembering which symbol meant less than and which symbol meant greater than.  One day, she had an epiphany.  If you make an L with your hand, it looks like the less than symbol.  Less than starts with L.  This was perfect!  

So, making a backwards L with your hand creates the greater than symbol.  If you are familiar with sign language, you could also make an argument that there are similarities between a sign language G and the greater than symbol.  

My student who discovered the hand trick was so proud of herself!  Her exact words were “This just made my day!”  And, she never had to ask me about what a symbol meant again.

Since then, I’ve been teaching this hand trick to my students.  After a couple of days, they usually get to where they just know what they symbol is without thinking about Ls and backwards Ls.

I had my students create the examples for each inequality symbol.  I would let one student pick the variable and another student pick the constant.  Some students were pretty mad at me because they didn’t get a chance to pick a variable for the class.  

We graphed each example and talked about the difference between open circles and closed circles.  My favorite discussion was on how to graph s is not equal to 3.

Updated Version of Inequalities Foldable

In 2017, I updated this foldable to include how to include an equal sign.

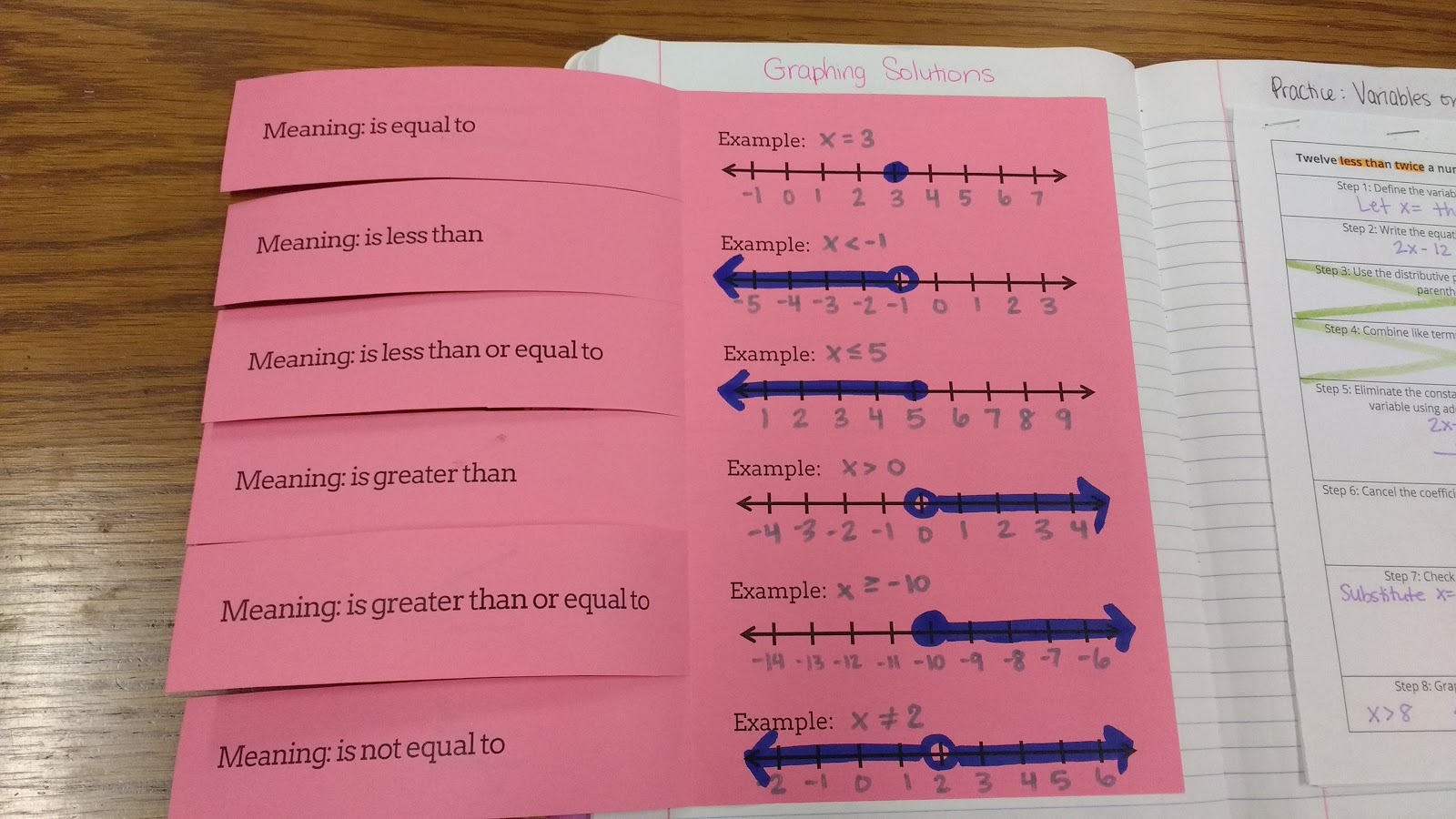
In the past, I did this without the equal sign. I’m SO thankful I finally found time to add the equal sign this year.

Flip Flop Rule for Inequalities

I teach my students that the order you write an inequality in matters.  Does it really?  No.  

However, on standardized tests, inequalities are always (almost always?) written with the variable first and constant last.  Of course, compound inequalities are the exception to this rule.  But, more about them later.  

As soon as I passed out this half-sheet of paper, I had the full attention and curiosity of my students.  Why are there flip flops on my paper?  Don’t you realize it’s winter?

I know, it’s a little corny, but I told that “If you have to flip flop the sides of the inequality (to achieve the correct order), you must also flip flop the inequality symbol.”  They affectionately called this the “Flip Flop Rule.”

This next page was attempt to modify the page I created last year for graphing two-variable inequalities.  I don’t like it quite as well, but I guess it did the job.

This probably isn’t the best thing to admit, but I didn’t teach my students why it was necessary to flip the inequality symbol when you multiply or divide by a negative last year.  

I mean, I taught them to do it.  I just never explained why.  This year, one of my Algebra 2 students asked.  I wrote 2 < 4 on the Smart Board.  Then, I divided both sides by -1.  If we keep the inequality symbol the same, we get -2 < -4 which is a false statement.  

Light bulbs went off.  It was a beautiful sight.  I am constantly becoming a better teacher.  I’ve heard before that experience is the best teacher.  I don’t think I quite realized how true that is until I started teaching.  

This year, I wrote 5, a large space, and a 7 on the board.  Then, I asked, “Who can tell me what symbol should go between these two numbers?”  The class agreed that a less than symbol belonged in the middle.  

Next, I asked for volunteers.  Tell me something we could do to both sides of this inequality.  Add 2.  So, we added 2 to both sides.  Guess what?  The inequality symbol is still true.  What else could we do to both sides of this inequality?  Subtract 7.  The inequality symbol is still correct.  

Give me something else we could do.  Multiply by 2.  The inequality symbol is STILL correct.  By now, my students were convinced that the inequality symbol would always remain the same.  So, I issued them a challenge.  

The first person to come up with an operation that would require us to change the inequality symbol would win a Tootsie Pop.  I bribe my students with A LOT of candy…

Solving and Graphing Inequalities Graphic Organizer

It took quite a while to come up with multiplying or dividing by a negative, but I like to think it was time extremely well spent.  

I must have still been half-asleep when I typed up these notes because I called it The Golden Rule of Inequalities: Whenever you multiply or divide both sides of an inequality by a negative number, you must flip the inequality symbol.  

In retrospect, the name makes no sense.  My kiddos didn’t seem to notice, though.

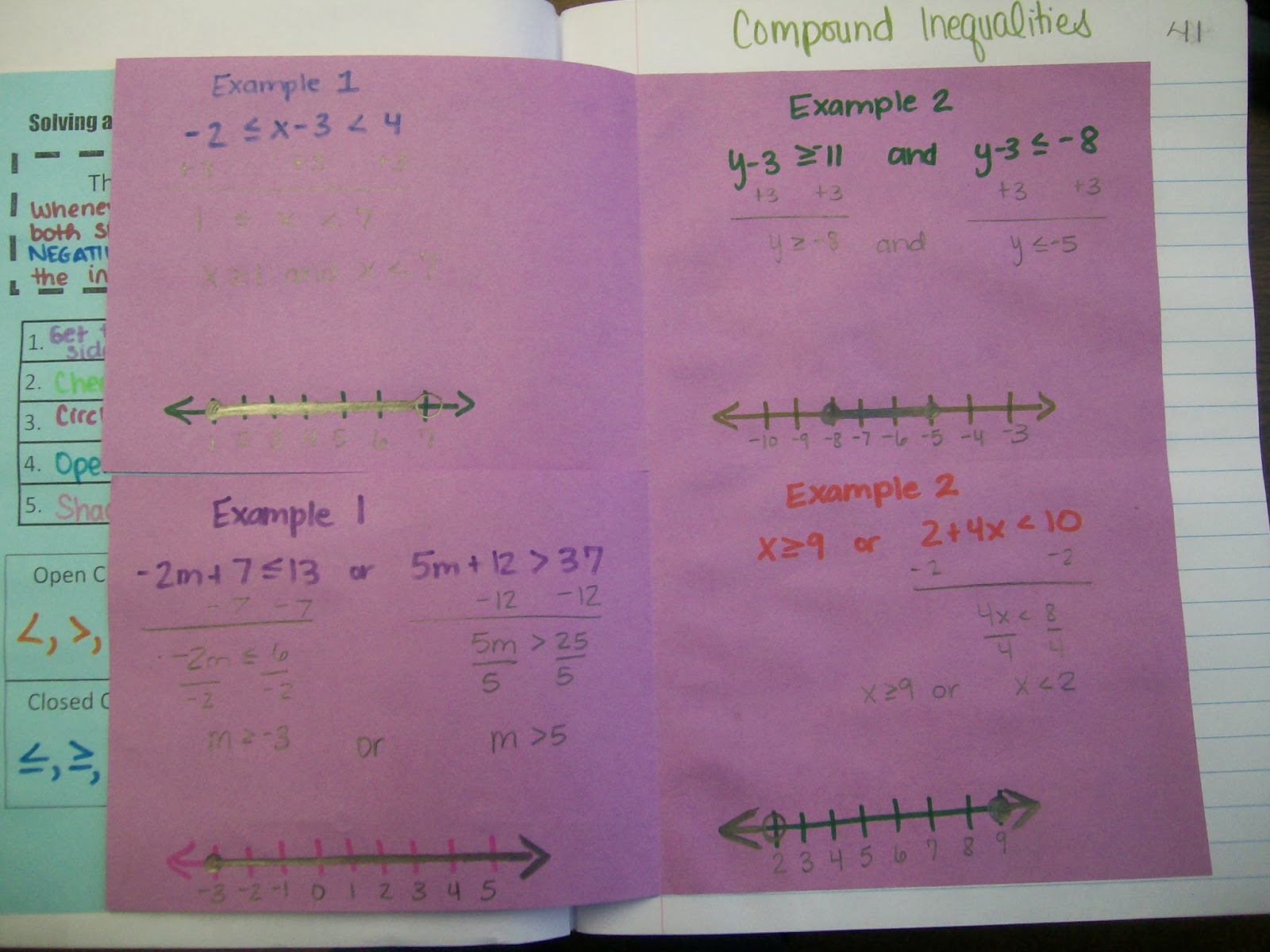
Compound Inequalities Foldable

The last part of our unit focused on compound inequalities.  I used the topic of Christmas presents to motivate the difference between AND and OR Compound Inequalities.  

After completing our bellwork, I sat down on my stool at the front of the classroom and announced, “Today we are going to talk about Christmas.”  I called on a student and asked them what was on their wishlist for Santa.  There were snickers.  I guess high school students are too cool for Santa Claus…

The first time I did this, I lucked out.  The first student I called on said that he wanted a PS4 or an X-Box One for Christmas.  I became incredibly excited and started peppering him with questions.  What gaming system do you currently have?  

If you get this new gaming system, will you have to get all new games or will your old games still work?  Finally, I asked him which system he was leaning towards.  “So, all you want for Christmas is an X-Box One?”  “You’d be happy if the only thing you got for Christmas was an X-Box One.”  See what I’m building towards here?

Does the gaming system do you any good if you don’t have any games to play?  So, I told him that what he really wanted was an X-Box One AND some games for Christmas.  Another student said my statement should actually say “I want an X-Box One, some games, AND some controllers for Christmas.”  

If you get the gaming system but no games, you will be disappointed.  If you get the games but no gaming system, you will be really disappointed.  The second time I did this during the day, I had to ask 3-4 students before I found someone that wanted a new gaming system for Christmas.  

With my last class of the day, I asked almost every single person in the class before I found someone who mentioned video games.  That was a shocker!

Then, I wrote an OR statement on the board.  I want an X-Box One or a PS4 for Christmas.  We had a similar conversation.  If this was your wish, would you be happy if you found an X-Box One under the tree?  

Would you be happy if you found a PS4 under the tree?  What if you found both under the tree?  With an AND statement, you had to get both of your wishes to be happy.  With an OR statement, you only have to get one of your wishes to be happy.  

If you get both of them, you will just be ecstatic.  This was the perfect transition for looking at AND and OR inequalities.

The inside of this foldable didn’t photograph the best where I wrote in pencil on this dark purple paper.  Sorry about that!

More Activities for Teaching One Variable Inequalities

• 
  Solving Equations/Inequalities with Variables on Both Sides Graphic Organizers
• 
  Compound Inequalities Graphic Organizers
• 
  Solving Equations/Inequalities with Variables On One Side Graphic Organizers
• 
  Inequalities Investigation
• 
  Graphing Solutions on a Number Line Speed Dating Activity
• 
  One Variable Inequalities Card Sort Activity
• 
  Compound Inequalities Foldable
• 
  Reviewing One Variable Inequalities
• 
  One Variable Inequalities Square Puzzle Activity
• 
  Graphing Inequalities Foldable
• 
  Inequalities Foldables