Balancing Act Puzzles
Today I want to highlight a collection of Balancing Act Puzzles from Heather Sparks. Heather is a bit of a legend in the world of Oklahoma math teaching. She was the 2009 Oklahoma Teacher of the Year. If you teach middle school math, her website is worth a browse. I am positive you will find multiple lesson ideas!
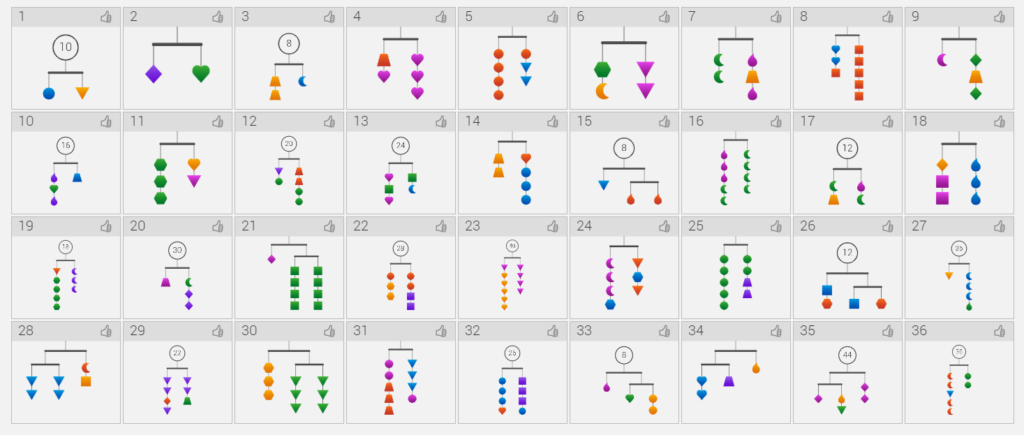
Heather has created a free PDF of 20 balance puzzles for teachers to use in their classrooms. These make a great bellwork activity. They are also a great addition to units on equations or systems of equations.
There are five levels of puzzles (levels A – E). The puzzles get progressively harder as the levels progress!
If you like these puzzles, you will also want to check out SolveMe Mobiles for an online interactive version of these puzzles.
More Resources for Teaching Systems of Equations and Inequalities
- Balancing Act Puzzles
- All Tied Up In Knots Systems of Equations Exploration Activity
- Solving Systems by Graphing Foldable
- Solving Systems by Elimination Graphic Organizer
- Solving Systems by Substitution Graphic Organizer
- Acrobats Grandmas and Ivan Systems of Equations Task
- Blank Graphic Organizers for Solving Systems of Equations Algebrically
- Writing Systems of Equations Foldable
- How Tall is Harold? Systems of Quadratics Task
- Systems of Equations Foldable
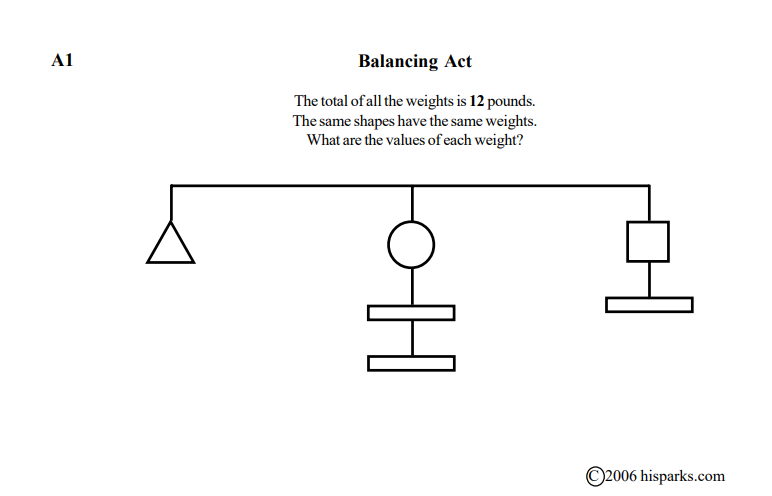
What do the center weights tell us in A1? Wouldn’t A1 have infinitely many solutions because the center weights do not affect the balance? Am I missing something? Could you email me the solution to the first puzzle so I can understand?
I just took a look at A1. I do believe there are multiple solutions. I don’t have an answer key since these puzzles are not my own creation.
The key is that the total of all weights is 12. So each of the three spokes/branches has to equal 4. The triangle weighs 4, the circle 2, the square 3, and the flat rectangles are 1 each.
The problem I see is that there is no statement saying that the 3 arms have to be equal, and one can only assume that the arms of the balance have to be equal. The other problem is that there is no statement saying that the objects have to have unique weights. So, you could have the arms each be 2, 3, or 4. If the arms are 2, the triangle would be 2, then the square and rectangle can both be one. The middle arm would have to be 8 to give a total of 12. This would make the circle 6. If the arms were both 3, the middle arm would be 6. There are actually 2 solutions then. Triangle 3, square 2, rectangles 1, circle 4. OR Triangle 3, square 1, rectangle 2, circle 2. All of this is based on the assumption that the objects cannot have zero as a weight. That opens up several other solutions.
All that being said, I think the assumption is that all the arms are to be equal and that none of the shapes are weightless. BUT that should really be stated explicitly in math problems.