|

Modeling Exponential Growth and Decay Activity with Skittles

Post Contents hide
1 Download Modeling Exponential Growth and Decay Activity with Skittles Foldable
2 More Resources for Teaching Exponential Functions

Today I’m sharing a creative way to use candy (in this case Skittles) for a modeling exponential growth and decay activity in Algebra.

modeling exponential growth and decay with skittles activity

Last summer, I attended several weeks of workshops and conferences.  At the first workshop of the summer, I got to participate in an activity that used M&Ms to model exponential decay.  I loved it, and I decided that it was definitely going to find a place in my lessons for the year.

At a different workshop, we did a very similar activity using M&Ms.  But, this time we modeled both exponential growth and exponential decay.  I was even more in love with the activity after this!

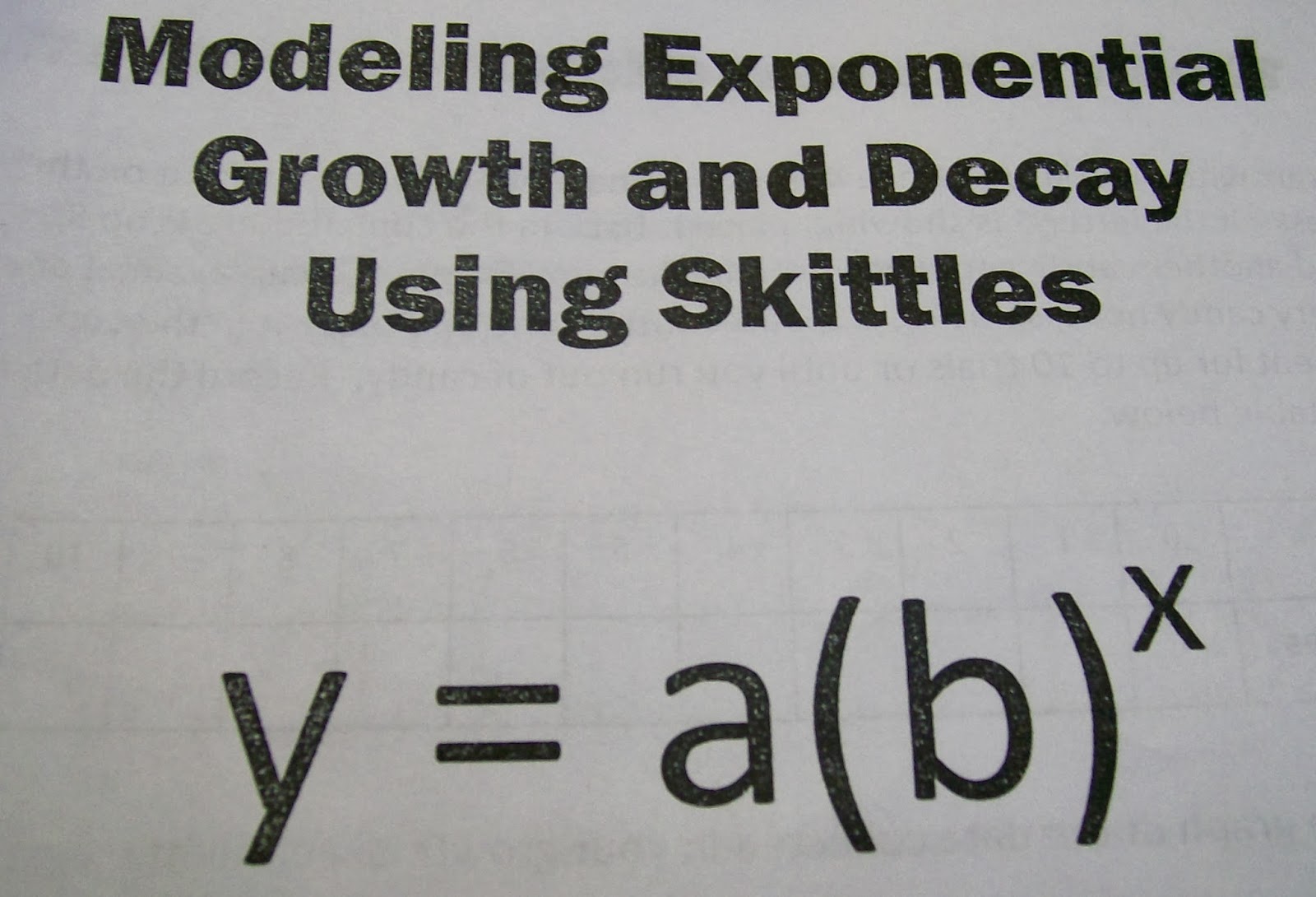
title of notes: modeling exponential growth and decay using skittles.

We have a student at our school with a severe peanut allergy, so I opted to use Skittles instead of M&Ms for this activity.

They say honesty is the best policy.  And, I really don’t have any reason to lie to you.  I want this blog to be an honest reflection of my teaching experience.  If something works well, I’m gonna share/brag about it.  If something doesn’t work well, I’m going to reflect on the experience and try to learn from it.

This is one of those activities that did not work well.  Okay, it was terrible.

Reasons why it bombed:

  • I did this lesson a Friday.  Students were already on weekend-mode.
  • This should have been a 2-3 day lesson.  Again, I was determined to fit this in on a Friday and start the new chapter on Monday.
  • My explanations could have been clearer.  My students really struggled with reading the instructions and following them on their own.
  • I should have given my students more practice with using their calculator’s regression capabilities BEFORE doing this activity. They had done linear regression a number of times. But, we had never done an exponential regression before on our graphing calculators.
  • I should have given them notes on how to perform an exponential regression in their notebooks that they could refer back to.
  • I spent the entire class period running around like a chicken with its head cut off.

Further proof that this activity needs some work:

Quote from student while doing another activity later in the year:

Is this really gonna be fun?  Because you said that skittles thing was going to be fun, and it wasn’t.

Last summer, I picked up these cute little bowls at Dollar Tree.  They were four for a dollar, and I just knew that I could find something to use them for in my classroom.  They made the perfect vehicle for holding each group’s Skittles.

small bowls from Dollar Tree.

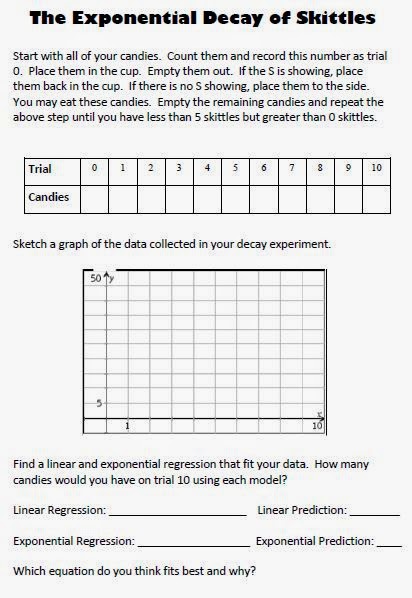
Each student was given a booklet foldable that had the instructions for both labs in it.  Below the instructions, there was room for students to create their table and graph.  They were asked to perform a linear and exponential regression in order to determine which regression best matched the data.  Way too many of my groups decided that the linear regression was the best fit.

Next year, I’m going to have to spend more time talking about how to determine which equation best fits the data.  I assumed that was a concept that my students would be able to intuitively understand, but I was wrong!  

Notes: exponential decay of skittles.
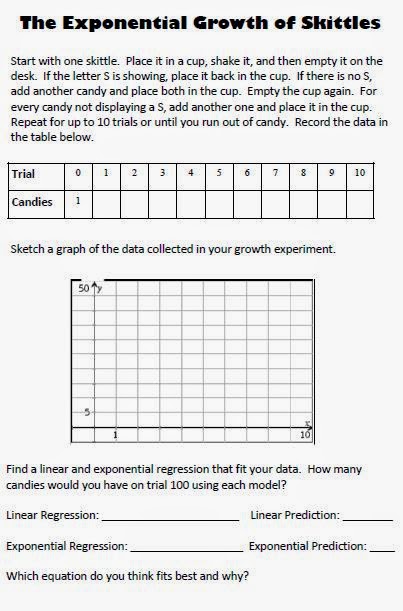
notes: exponential growth of skittles.

Each group was asked to wash their hands or use hand sanitizer before starting!  They were given a bowl, a bag of Skittles, and a paper plate.

skittles in small baskets from dollar tree.

Following the instructions in the exponential decay lab, they shook their bowls of skittles, poured them out, looked to see which ones did and did not have an S showing. These were removed from the activity.

skittles on paper plate.

I asked students to write down three things they learned while doing this activity.

3 Things I learned today section of notes.

Download Modeling Exponential Growth and Decay Activity with Skittles Foldable


Skittles Exponential Growth and Decay Activity (PDF) (2074 downloads )


Skittles Exponential Growth and Decay Activity (Editable Publisher File ZIP) (1372 downloads )

More Resources for Teaching Exponential Functions

Sarah Carter teaches high school math in her hometown of Coweta, Oklahoma. She currently teaches AP Precalculus, AP Calculus AB, and Statistics. She is passionate about sharing creative and hands-on teaching ideas with math teachers around the world through her blog, Math = Love.

Similar Posts

9 Comments

  1. Hi Sarah,

    I just discovered your month a few months ago and have found some great inspiration! I coach HS teachers and this activity got me really excited. In 5 years of teaching, I haven't seen this exponential activity and LOVE it. I've adapted your investigation to be a mix of what I see here and another version I found online. If you're interested, I'll send you what I did !

    Thanks! Have a good day!
    Jaclyn

    1. Jaclyn,

      I'd LOVE to see your adaptation! My e-mail is mathequalslove (at) gmail (dot) com

      Thanks!

  2. Sarah,
    Would you do the exponential growth activity first, and then use the same candies again for the decay activity? Or do you have two sets of candies, one for each activity?

    This reminds me of a similar activity done with pennies, modeling the half-life of an imaginary element "Lincoln-ium" that I've done with Chem and Physical Science classes. Start with a 100 pennies in a shoe box, cover and shake for 10 seconds, open and remove all coins not displaying Lincoln's profile. Repeat. Use data to create a decay curve and find the half-life, letting 1 second=1 day or 1 year.

    1. Hmm… I didn't think about the issue of using the candies over multiple days. Since we rushed through both activities in the same day, we used the same candy. I like the idea of using the pennies! It might work to use candies one day and pennies the next.

      Thanks for sharing!

  3. Sarah,

    I had two specific questions about your use of skittles. 1) Were there a lot of missing S's on the Skittles? I poured a small snack size bag of like 12 and at least 3-4 were missing or VERY hard to see. And 2) Do you think the shape changes the relationship? I noticed that your kids concluded linear more often and I was wondering if it was because the actual data looked more linear than exponential.

    I've always used M&M's but I have a kid with peanut allergies and would like to try to use Skittles instead, but the two questions mentioned above make me a little nervous.

    Thank you for your awesome blog!

    1. I did have a few issues with missing letters. I learned this the hard way. I'd definitely have students check all their skittles in the future.

      I think having them estimate the number of skittles led to them thinking it was linear. I'm not sure how much they actually looked at the shape of the data.

      I think I'd do a lot of things differently with this activity in the future.

  4. Ok, so I'm going to modify this for my 8th grade algebra class. Approximately how many skittles did you have available per student?

    1. Maybe 30 or so per group? You could probably still make it work with 20.

Comments are closed.