Factoring Quadratics Graphic Organizers
Today I want to share some graphic organizers I created to remind students the steps for factoring quadratics. We filled these out and glued them in our algebra interactive notebooks.
This year, I am taking a big risk with my Algebra 1 kiddos. I taught them to factor quadratic trinomials with a leading coefficient greater than one before we ever discussed solving equations.
Last year, I crammed in factoring quadratics at the very end of the school year. I was feeling rushed, and I needed to cover factoring quadratics and simplifying radicals before the end-of-instruction exam. I didn’t feel like I really did either topic justice because I was so rushed.
This year is different. Really different. My Algebra 1 students came in at a much lower level than my students last year.
After spending weeks on integer operations and the order of operations and all that fun stuff that students should already know from middle school, I still had a lot of kids who were just not getting it. That was nothing new.
Last year, my students struggled with these topics, too. And, last year, I moved on to solving equations and HOPED that the rules for dealing with integers and all that good stuff would “click” when they started seeing it in equations. That worked to a certain extent.
This year, I could tell I was more frustrated and my students were more frustrated than normal. The kids who understood integer operations were bored out of their minds.
They wanted to move onto something new. The kids who didn’t understand integer operations still didn’t quite know that they didn’t understand them. So, my constant review as futile.
My students had solved equations in middle school, so that wouldn’t be something new and exciting. After teaching them the distributive property, I had an epiphany.
I made a commitment to myself last year that I would stop teaching students to FOIL. I learned to multiply binomials by FOILing. But, I’m learning that some of the tricks that I was taught in Algebra are just that.
They are tricks that work, but students don’t quite know why they work. If my students can see a problem as an extension of the distributive property, they can solve a myriad of problems in different forms.
If students only know how to FOIL, they are going to be stuck and not know what to do when they are asked to multiply a trinomial and a binomial.
Last year, instead of teaching students to FOIL, I taught students what I called “The Double Distributive Property.” This could be extended to the triple distributive property as well. And, it worked out pretty well.
What if I didn’t teach the double distributive property as a separate property? What if just told my students that when they see two polynomials being multiplied together that it is a distributive property problem?
So, I did just that. Day one of the distributive property featured monomials times binomials. Day two of the distributive property featured polynomials times polynomials. I made no distinction between the two.
When my students see two polynomials being multiplied, they automatically think distributive property. And, that makes me insanely happy.
Factoring Quadratic Trinomials with a Leading Coefficient of 1
After teaching students to distribute, the natural thing to teach students is to undistribute, or factor.
When my students were first reviewing integer operations, I gave them a sheet of diamond puzzles or X-puzzles to complete. I taught my students to factor quadratics with a leading coefficient of 1 using the X-puzzle.

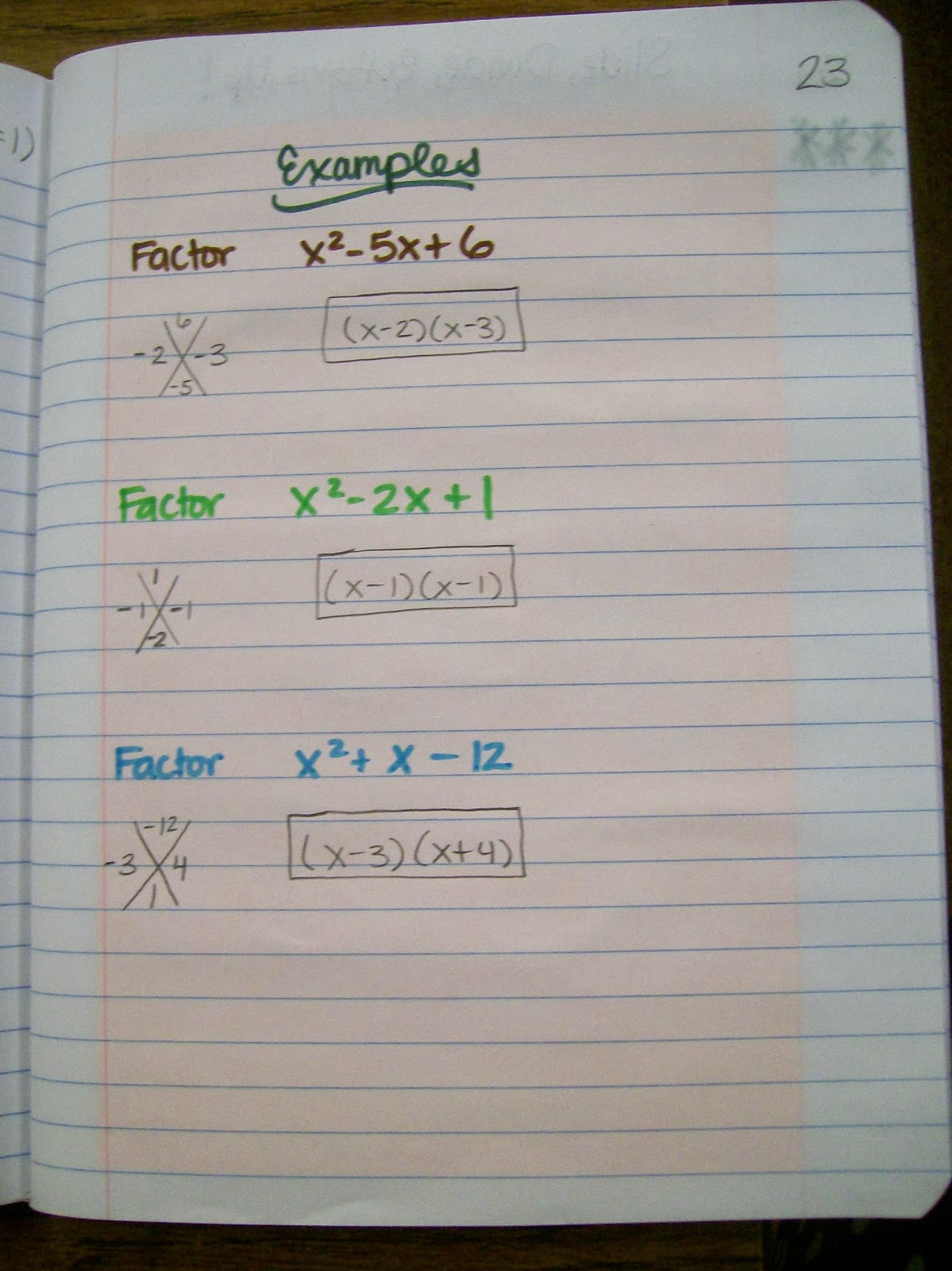

Factoring Quadratic Trinomials with a Leading Coefficient Greater than One
This more affectionately known as Slide, Divide, Bottoms UP!
Again, I changed my teaching approach from last year. Last year, I taught my students to do the Airplane Method. This worked. But, I still had a few students who never caught on.
This summer, at the Common Core conference I went to, I was introduced to the Slide and Divide method of factoring. Another teacher mentioned that she called it the Bottoms Up Method.
I combined these two ideas to create the “Slide, Divide, Bottoms Up!” Method. My students LOVE it.
Yes, this is a trick. But, I haven’t figured out a better way to teach it. When I took Algebra 1, I learned the guess and check method. And, I found that method to be torturous. But, I didn’t know there was a better, faster, easier way. Now that I do know there is a better way, I would never go back.
Please, please, please do not use this slide, divide, bottoms up method with your students. I now know better, and I don’t want you to be led astray by my new teacher enthusiasm for a factoring trick.
I assumed that because the trick was shared at a workshop for teachers that it was a recommended method for using in the classroom. I was wrong. There is a better way if you don’t want to teach the guess and check method.
It’s called the box method (or area model.) It works for ALL types of factoring problems. It is much more conceptual, and I have found that students actually understand what they are doing instead of rotely following an algorithm that you have asked them to memorize.
Plus, the amazing thing about the box method is that you can even use it to divide polynomials!

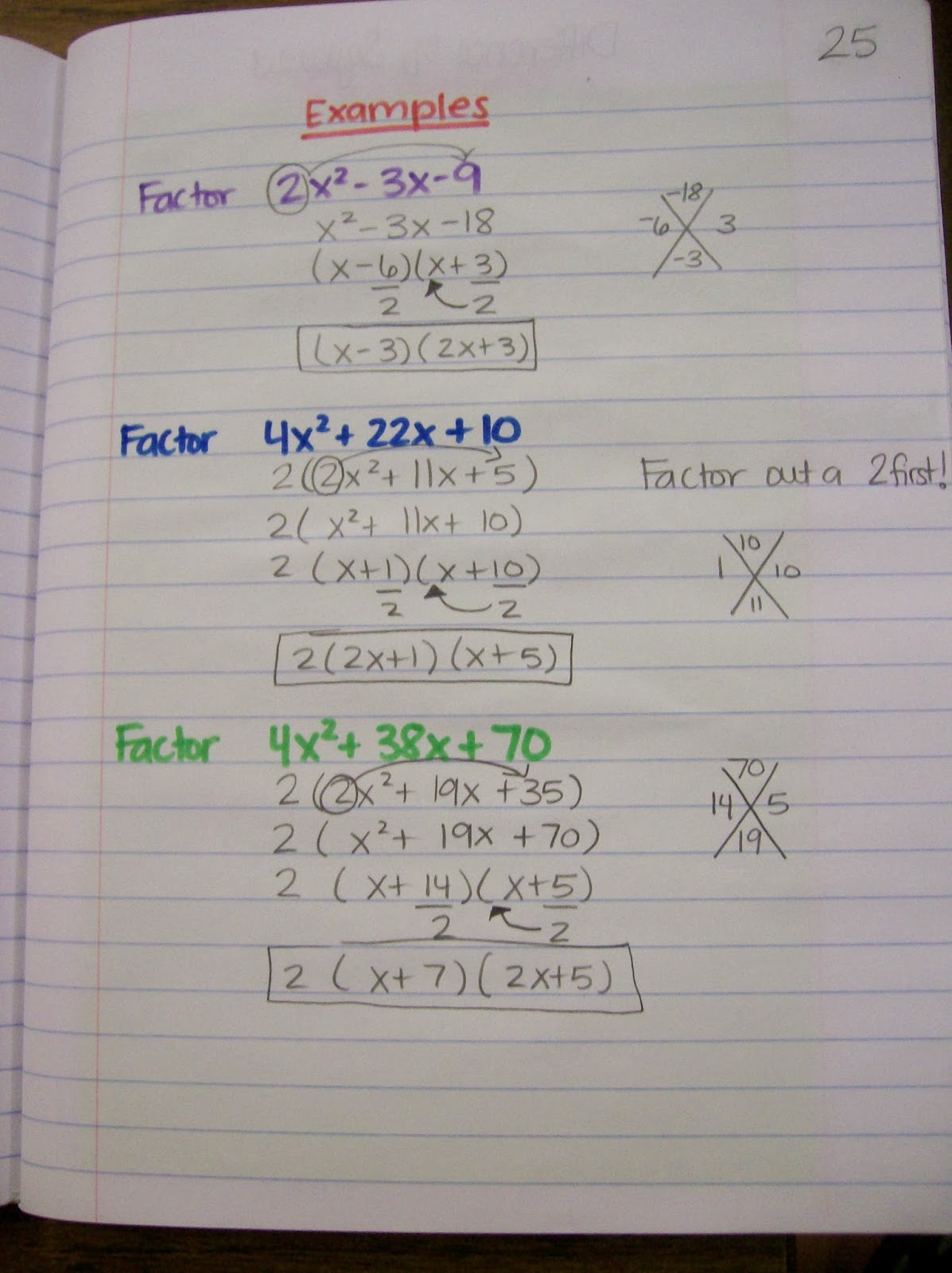

Factoring Difference of Squares

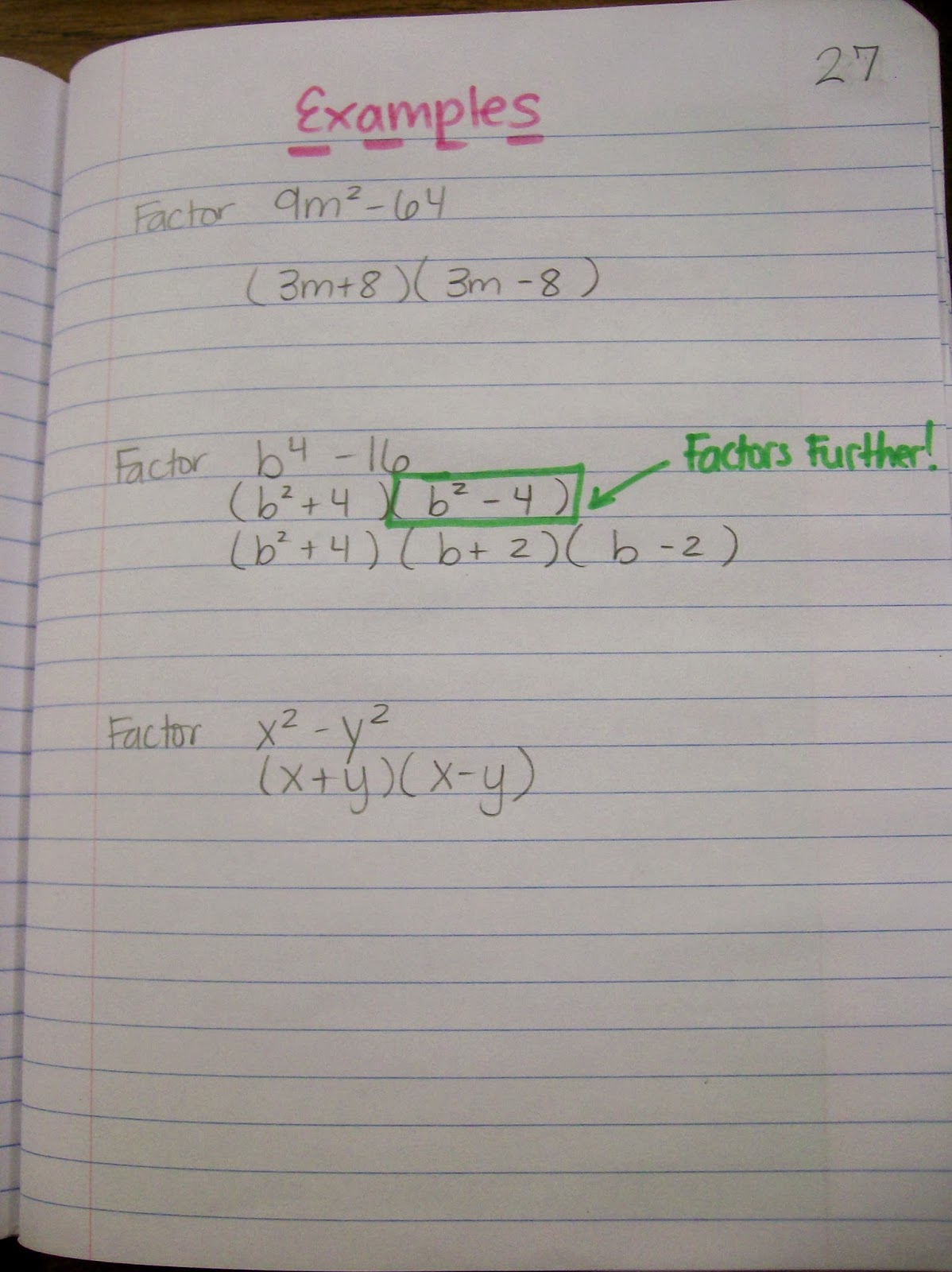

Free Download of Factoring Quadratics Graphic Organizers
Factoring when a is 1 Graphic Organizer (PDF) (2674 downloads )
Factoring when a is greater than 1 Graphic Organizer (PDF) (2548 downloads )
Factoring Difference of Squares Graphic Organizer (PDF) (2087 downloads )
Looking for resources to give students practice with factoring? I recommend checking out this Factoring Puzzle.
More Resources for Teaching Quadratics
- Quadratic Formula Activities
- Factoring Activities
- Speedy Squares Activity for Quadratic Regression
- X Puzzles Factoring Review Game
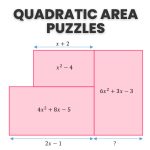
- Quadratic Area Puzzles
- Factoring Puzzle for Quadratic Trinomials
- Shared Factors – A Quadratics Puzzle
- Factoring Quadratics Practice Activity (When a = 1)
- If the IRS had discovered the quadratic formula…
- Area Model Puzzles from Christie Bradshaw
- ZERO Game to Introduce Factoring Quadratics
- Vertex Form of a Quadratic Card Sort Activity















I have read your post on teaching factoring using slide, divide, bottoms up and am intrigued. I've always used the AC method using factoring by grouping. Now that you've taught factoring using several methods, which do you prefer or do you teach them all?
Not crazy about slide and divide. Seems like a trick without logical mathematical steps
I have moved away from using it and now use the box method for this reason.
I’ve also used the box method to teach factoring quadratics to my kids. However when some students have been taught to guess and check, they find this method tedious, its tough to get them to buy into more writing sadly. I love it … learned it over 10 years ago. I prefer giving my kids an algorithm to follow, I loathe “guess and check”. I found the box method on the purplemath website. Absolutely love it!
I also came across the “split the middle” method along with the X-Box or Diamond Puzzle. I love teaching it this way, as it involves concrete steps my kids can “see” and so it provides an algorithm they can practice and master. 🙂