Speedy Squares Activity for Quadratic Regression

Post Contents hide

1 Free Download of Speedy Squares Activity for Quadratic Regression

2 More Activities for Teaching Regression

This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.

Want to check out my favorite Amazon items for the classroom? Check out my Amazon favorites page!

I was so excited to discover this Speedy Squares Activity for practicing quadratic regression several years ago. I have used it successfully with my Algebra 2 classes in the past. Sadly, regression is one of the topics we did not get to fully explore in Algebra 2 this past year due to losing so much instructional time due to COVID.

Speedy Squares is the creation of Mary Bourassa. I highly recommend reading through Mary’s explanation of the activity. Her blog chronicles her classroom on a daily basis, and I highly recommend it!

Speedy Squares Activity for Quadratic Regression

The goal of the Speedy Squares Activity is to use mathematics (quadratic regression) to determine how long it would take to build a 26 x 26 square out of linking cubes.

If you don’t have a class set of linking cubes (or snap cubes), you are missing out on awesome activities like this or Fawn Nguyen’s Hotel Snap! I also recommend checking out Build It, a great team building activity for the first week of school that uses linking cubes.

For this activity, I put students in groups of 3. Each group member had a specific role to play during the data collection portion of this activity. The three jobs were builder, timer, and recorder/cube manager.

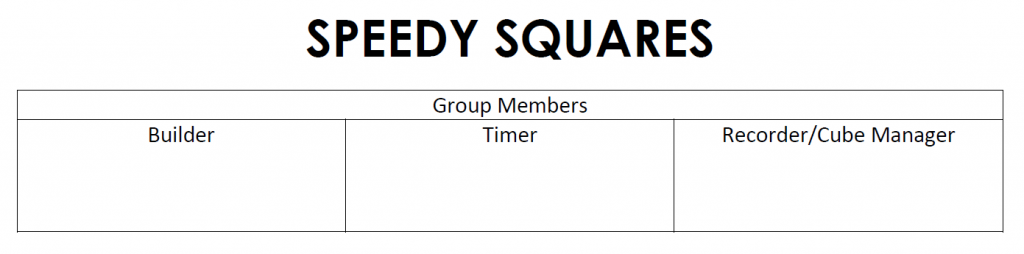
Group Member Jobs for Speedy Squares Activity for Quadratic Regression

The builder was responsible for building various squares of different side lengths using the linking cubes. The timer was responsible for timing the builder. The recorder/cube manager had two jobs. First, they were responsible for getting the linking cubes for their group and returning the linking cubes when they were done. Secondly, they recorded the times measured by the timer.

Students working with linking cubes for speedy squares activity.

Before groups began their data collection, I asked them to come up with a group estimate of how long they thought it would take to build a 26 x 26 square out of linking cubes. Then, we had a class discussion of why it would be useful to use mathematics to solve this question instead of just building a 26 x 26 square and timing ourselves.

We ended up discussing things such as the fact that Mrs. Carter doesn’t have enough linking cubes to build a 26 x 26 square. Also, timing the building of a 26 x 26 square would only give us one piece of data. A mathematical model, on the other hand, could be used to find the time for any dimension of our choosing.

I couldn’t find Mary Bourassa’s handout online, so I retyped it myself with a few small changes.

Activity Page for Speedy Squares Activity.

My students really enjoyed this data collection activity. Their results made some pretty nice parabolas, and it gave them good practice performing regression with either their graphing calculator or Desmos.

Students working on speedy squares activity.

I didn’t have quite as many linking cubes as I needed, so groups had to combine their linking cubes with another group to have enough for the last data point. It ended up working out just fine. I used to have a lot more linking cubes, but they were purchased with grant money by my previous school. I was very sad to have to leave them behind!

One of my groups didn’t have the best data. I think their building method continually got better and better as they collected more data. It led to a very wonky looking data set.