Graphing Inequalities Foldable
This graphing inequalities foldable was inspired by a foldable I saw on Coffee Cups and Lesson Plans.
I started this unit by drawing the different inequality symbols on my Smart Board. I wrote numbers above each symbol. Then, I asked a simple question, “Who can tell me which number is above the symbol that means less than?”
Hands shot up in the air. Some students gave me the correct number. Others had confused the symbol for less than with the symbol for greater than. Still others had confused it for the less than or equal to symbol.
One student argued that there was no way of knowing because there were no numbers for the alligator to eat.
Graphing Inequalities Foldable

Oh, the alligator. I remember learning about the alligator in elementary school.
The alligator is a really hungry animal. He always chooses to eat the largest number of fish possible. I even did a project for my ed psych class in college where I taught a kindergartner about inequality symbols using the alligator.
Now that I’m teaching algebra, I can’t stand the alligator. The alligator doesn’t help my students translate symbols into words. The alligator holds my students back. So, I told them that they had to take everything they ever learned about the alligator and throw it out the window.
I thought there was going to be a revolt in my classroom. One student proclaimed, “That’s half of my life! You can’t expect me to just throw away half of my life because you don’t like the alligator.”
When I look at an inequality symbol, I just know its name. I guess I just memorized them somewhere along the way without realizing it.
Last year, one of my college algebra students was having a terrible time remembering which symbol meant less than and which symbol meant greater than. One day, she had an epiphany. If you make an L with your hand, it looks like the less than symbol. Less than starts with L. This was perfect!
So, making a backwards L with your hand creates the greater than symbol. If you are familiar with sign language, you could also make an argument that there are similarities between a sign language G and the greater than symbol.
My student who discovered the hand trick was so proud of herself! Her exact words were “This just made my day!” And, she never had to ask me about what a symbol meant again.
Since then, I’ve been teaching this hand trick to my students. After a couple of days, they usually get to where they just know what they symbol is without thinking about Ls and backwards Ls.

I had my students create the examples for each inequality symbol. I would let one student pick the variable and another student pick the constant. Some students were pretty mad at me because they didn’t get a chance to pick a variable for the class.
We graphed each example and talked about the difference between open circles and closed circles. My favorite discussion was on how to graph s is not equal to 3.
Updated Version of Inequalities Foldable
In 2017, I updated this foldable to include how to include an equal sign.

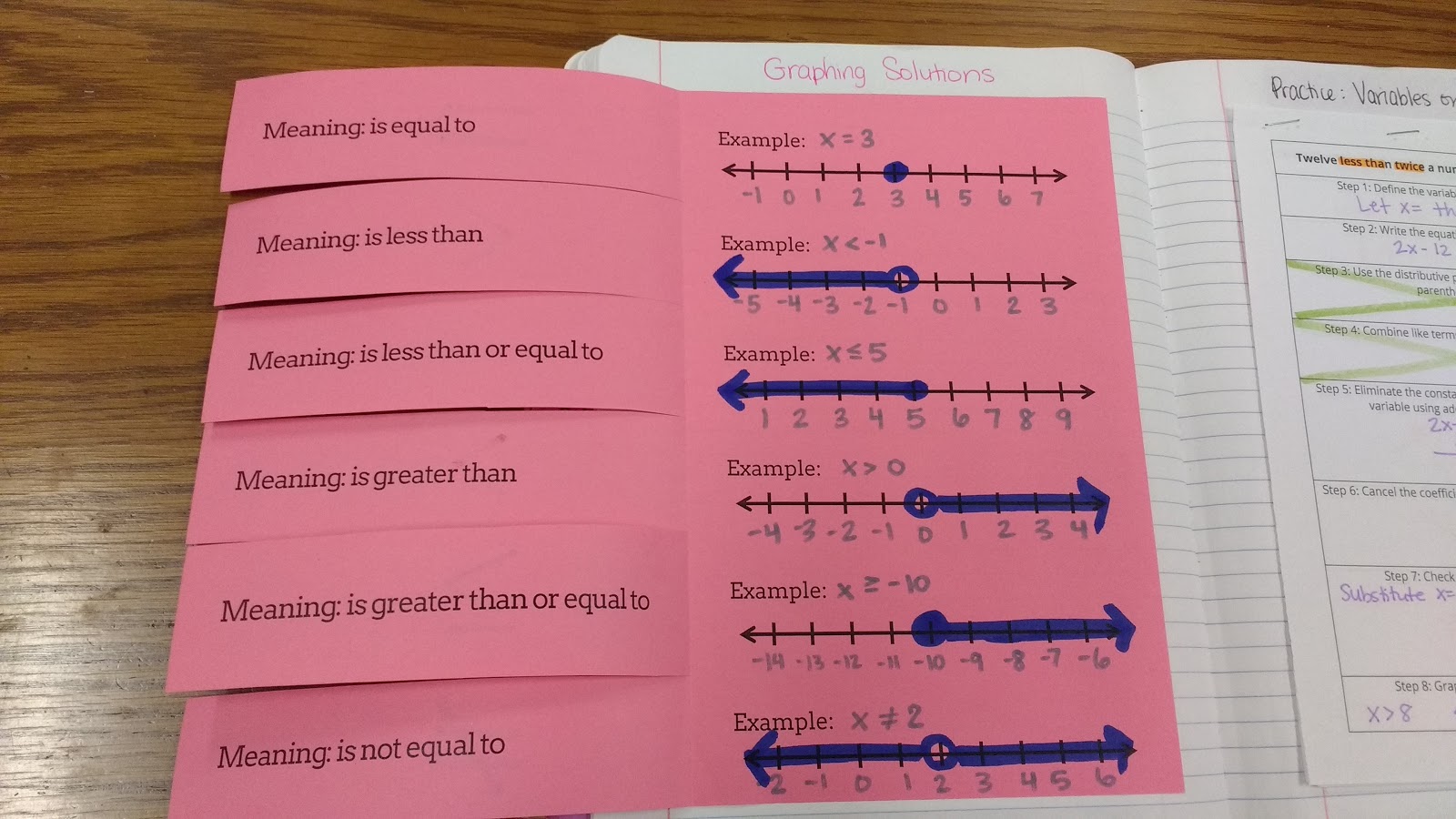
In the past, I did this without the equal sign. I’m SO thankful I finally found time to add the equal sign this year.
Flip Flop Rule for Inequalities
I teach my students that the order you write an inequality in matters. Does it really? No.
However, on standardized tests, inequalities are always (almost always?) written with the variable first and constant last. Of course, compound inequalities are the exception to this rule. But, more about them later.
As soon as I passed out this half-sheet of paper, I had the full attention and curiosity of my students. Why are there flip flops on my paper? Don’t you realize it’s winter?
I know, it’s a little corny, but I told that “If you have to flip flop the sides of the inequality (to achieve the correct order), you must also flip flop the inequality symbol.” They affectionately called this the “Flip Flop Rule.”

This next page was attempt to modify the page I created last year for graphing two-variable inequalities. I don’t like it quite as well, but I guess it did the job.
This probably isn’t the best thing to admit, but I didn’t teach my students why it was necessary to flip the inequality symbol when you multiply or divide by a negative last year.
I mean, I taught them to do it. I just never explained why. This year, one of my Algebra 2 students asked. I wrote 2 < 4 on the Smart Board. Then, I divided both sides by -1. If we keep the inequality symbol the same, we get -2 < -4 which is a false statement.
Light bulbs went off. It was a beautiful sight. I am constantly becoming a better teacher. I’ve heard before that experience is the best teacher. I don’t think I quite realized how true that is until I started teaching.
This year, I wrote 5, a large space, and a 7 on the board. Then, I asked, “Who can tell me what symbol should go between these two numbers?” The class agreed that a less than symbol belonged in the middle.
Next, I asked for volunteers. Tell me something we could do to both sides of this inequality. Add 2. So, we added 2 to both sides. Guess what? The inequality symbol is still true. What else could we do to both sides of this inequality? Subtract 7. The inequality symbol is still correct.
Give me something else we could do. Multiply by 2. The inequality symbol is STILL correct. By now, my students were convinced that the inequality symbol would always remain the same. So, I issued them a challenge.
The first person to come up with an operation that would require us to change the inequality symbol would win a Tootsie Pop. I bribe my students with A LOT of candy…
Solving and Graphing Inequalities Graphic Organizer
It took quite a while to come up with multiplying or dividing by a negative, but I like to think it was time extremely well spent.
I must have still been half-asleep when I typed up these notes because I called it The Golden Rule of Inequalities: Whenever you multiply or divide both sides of an inequality by a negative number, you must flip the inequality symbol.
In retrospect, the name makes no sense. My kiddos didn’t seem to notice, though.

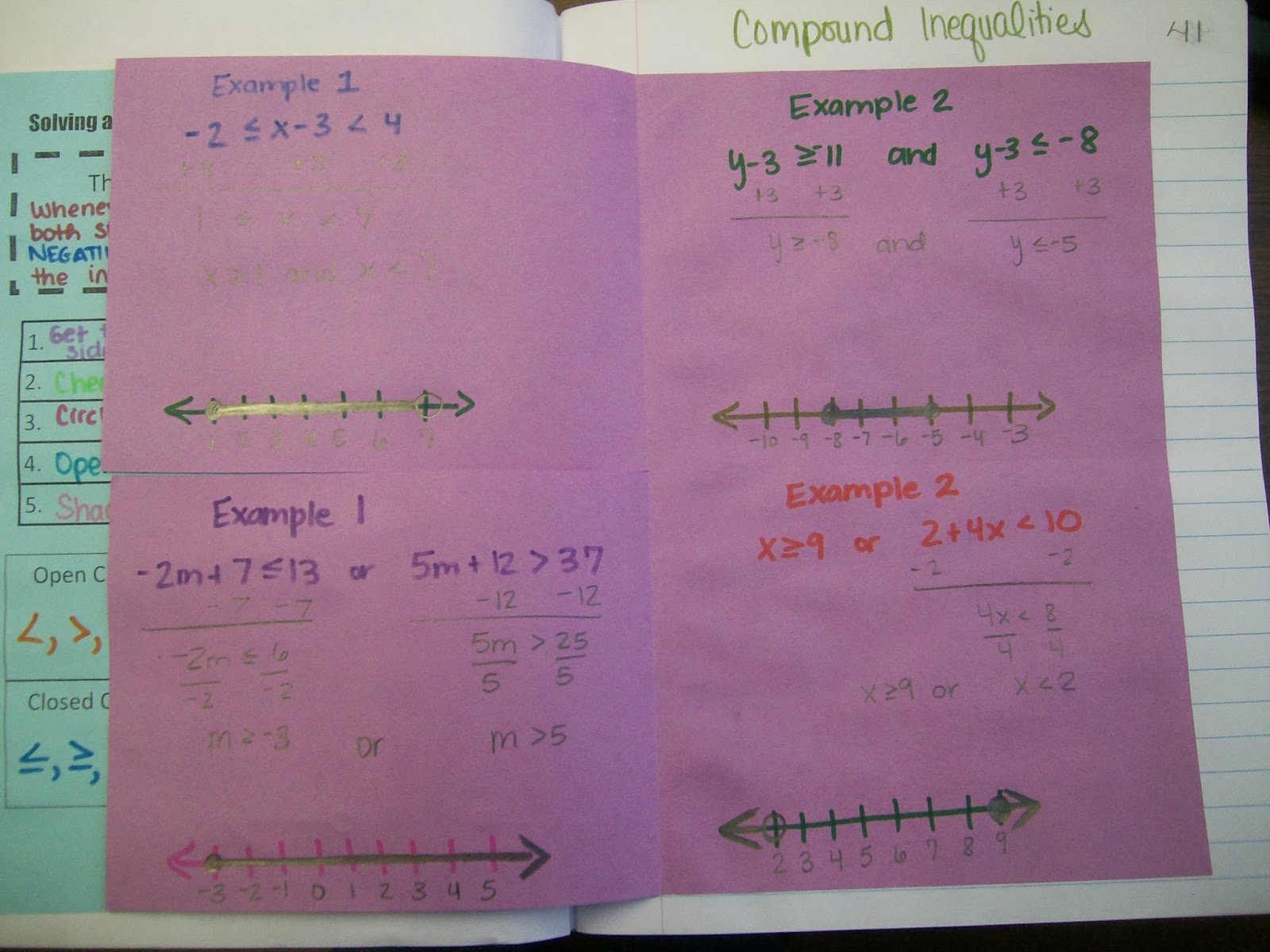
Compound Inequalities Foldable
The last part of our unit focused on compound inequalities. I used the topic of Christmas presents to motivate the difference between AND and OR Compound Inequalities.
After completing our bellwork, I sat down on my stool at the front of the classroom and announced, “Today we are going to talk about Christmas.” I called on a student and asked them what was on their wishlist for Santa. There were snickers. I guess high school students are too cool for Santa Claus…
The first time I did this, I lucked out. The first student I called on said that he wanted a PS4 or an X-Box One for Christmas. I became incredibly excited and started peppering him with questions. What gaming system do you currently have?
If you get this new gaming system, will you have to get all new games or will your old games still work? Finally, I asked him which system he was leaning towards. “So, all you want for Christmas is an X-Box One?” “You’d be happy if the only thing you got for Christmas was an X-Box One.” See what I’m building towards here?
Does the gaming system do you any good if you don’t have any games to play? So, I told him that what he really wanted was an X-Box One AND some games for Christmas. Another student said my statement should actually say “I want an X-Box One, some games, AND some controllers for Christmas.”
If you get the gaming system but no games, you will be disappointed. If you get the games but no gaming system, you will be really disappointed. The second time I did this during the day, I had to ask 3-4 students before I found someone that wanted a new gaming system for Christmas.
With my last class of the day, I asked almost every single person in the class before I found someone who mentioned video games. That was a shocker!
Then, I wrote an OR statement on the board. I want an X-Box One or a PS4 for Christmas. We had a similar conversation. If this was your wish, would you be happy if you found an X-Box One under the tree?
Would you be happy if you found a PS4 under the tree? What if you found both under the tree? With an AND statement, you had to get both of your wishes to be happy. With an OR statement, you only have to get one of your wishes to be happy.
If you get both of them, you will just be ecstatic. This was the perfect transition for looking at AND and OR inequalities.

The inside of this foldable didn’t photograph the best where I wrote in pencil on this dark purple paper. Sorry about that!




Sarah,
These are fantastic! We already learned inequalities, but I may go back and use some of these. The flip flop is my favorite. Thanks so much!
You're welcome! Thanks for the feedback!
If you have the variable first, the inequality points in the same direction as the arrow on your number line.
Exactly! I was proud of myself this year for not telling my students this fact. Instead, I waited until one of my students figured it out. Then, she was able to teach her "shortcut" to the entire class. It achieved the same purpose, but I like to think that they will remember it better because they learned it from a classmate. And, I know the student who discovered it will never forget it!
Hello,
Where do you find your templates?
Hi! Thanks for reading my blog! I make most of my templates myself using Microsoft Publisher or Open Office Draw. If I use someone else's template, I always try to link to the source.
Thank you! I am a first year teacher, and I can't wait to use these tomorrow! 🙂
You're welcome! I hope your first year of teaching is going well! Thanks for reading my blog!
Sarah,
Can you please email me these pdfs? kburnette@bcpschools.org
Thank you,
Kelly
Love the foldables. The flip flop is fabulous! I can't wait to use these!
Thanks! The flip flop was a last minute idea that I *think* was successful at making the rule just a bit more sticky for my students.
I like to call flipping the inequality sign "The Big But Theorem". I say okay today we are going to learn about the big but theorem. They get really excited and laugh because they are teenagers and are thinking butt not but. I write on the board, solving inequalities is just like solving equations BUT (in HUGE letters) when we multiply or divide by the negative we have to flip the sign. They love it.
I'm totally stealing this for next year! Thanks for sharing!
Thanks, as always, for sharing generously. Whenever I Google a topic and the word "foldable" I always seem to end up here. 🙂 The flip flops are cute! One of my colleagues uses a poster of Flipper, but I really doubt that many kids know who Flipper is. So, I took your idea of the flip flop and ran with it, turning the clip art sideways so the students can write in both instances of when they would change the signs.
One of my coworkers told me the same thing the other day! "Do you realize that your name pops up every time I google for a foldable?!?" I love your twist on the flip flops. Genius!
Hi,Sarah. I really enjoyed your blog, but I was not able to see the documents. My email address is niwhite524[at]gmail.com. Thanks for the excellent ideas!
E-mail sent. Thanks for stopping by my blog! If you need help with anything else, please let me know!
I couldn't see all the documents as well. Could you send me an email with all of these wonderful ideas! leandra.london@ops.org
I couldn't see the documents either. I'd love if you could attach them to an email to drichardson@mcpsva.org. Thanks so much!!!
Thank you. These are so useful, and you are so generous.
would you mind send me the templates you have for your inequality lesson? I can't seem to download them. Thank you so much!
e-mail: pamrudd[at]hotmail.com
Sarah, would you please email me all of these wonderful ideas at patterss1@highlands.k12.fl.us?
Thank you,
Sheri
I love your templates for teaching inequalities! I am going to use these with my 7th graders next week. Could you please email me the templates, I was unable to open them from here. thanks smib@bcswan.net
Thank muchly for sharing your resources and ideas. My students will enjoy them.
You're very welcome! Hope you and your students enjoy them!
Please send me the files – shookcm@ccps.k12.va.us THANK YOU SO MUCH! These are great!
I love the flip flop idea too. Would you mind sending me the pdf? Thank you!
rhonda.kinley@vbschools.com
Can you send me the templates to these items? I plan on using them for my Pre-Algebra class that I am teaching at the HS next year. Thanks for everything. lisa.duerksen@usd262.net
Sent!
Thank you for making your files available! I love your ideas!
You're very welcome!