| | | |

Is it Possible Divisibility Puzzle

This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.

This divisibility rules puzzle is called “Is It Possible?” and it’s a real stumper!

Is It Possible Divisibility Puzzle

Instructions

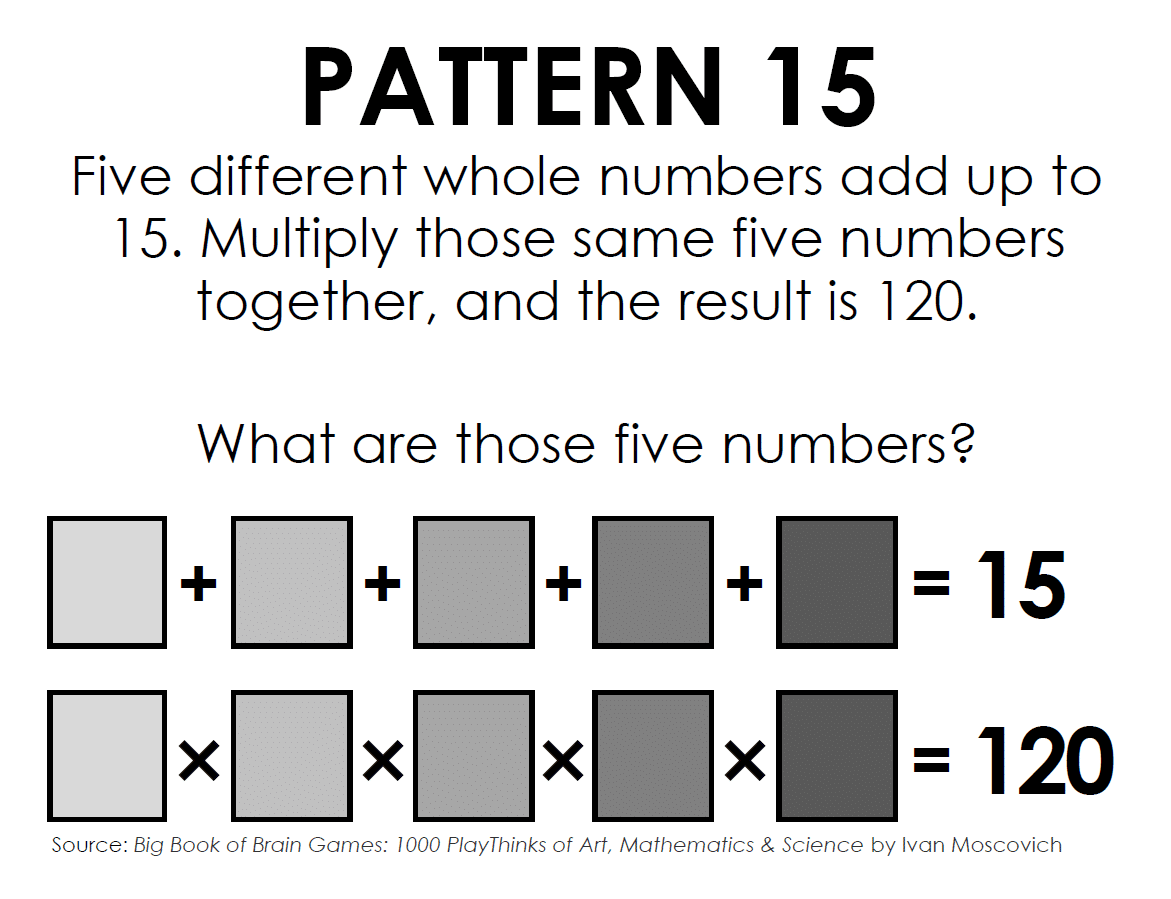
Is it possible to use the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0 to construct a ten-digit number divisible (without a remainder) by all the numbers from 2 to 18?

If so, construct the ten-digit number. If not possible, explain why this cannot be done.

Puzzle Source

I ran across this divisibility puzzle in a copy of The Giant Book of Hard-to-Solve Mind Puzzles. I picked up my copy at Goodwill for $2.

It turns out that this book is out of print which makes used copies from Amazon VERY expensive. If you happen upon a copy of this book at a thrift store or used book shop, it’s definitely worth picking up a copy!

This is actually the third puzzle I’ve created for my classroom based on this book. Previously, I have shared the 12 Envelopes Puzzle and 9 Squares Puzzle from this same book.

Using This Puzzle in the Classroom

When I ran across this divisibility rules puzzle, I knew that it would make a lovely magnetic puzzle to post on my dry erase board for the upcoming year. I’m making it my goal to post a new puzzle on the board each week.

I don’t have space for a puzzle table like I had in the past at my old school (that’s what happens when you have 30 students crammed into a classroom), so I’ve found that the best way to engage students in puzzles is to make them vertical by posting them on the dry erase board.

The board is magnetic, and I’ve found I get the most engagement from students when the puzzles involve magnetic pieces that can be manipulated.

I plan on putting disc magnets on the back of each digit. My magnets are currently locked away in my classroom, so that will probably have to wait until August.

Another Divisibility Puzzle

If you like this puzzle, you might also want to check out my printable divisibility puzzle.

Divisibility Puzzle in Binder.

Divisibility Rules Chart

If your students need a reminder of basic divisibility rules, I have a printable divisibility rules chart that can be used as a reference.

divisibility rules printable chart pdf.

Puzzle Solutions

ANsWer key link

Puzzle solutions are available on a password-protected solution page. I do not openly post the puzzle answer keys because one of my goals as a resource creator is to craft learning experiences for students that are non-google-able. I want teachers to be able to use these puzzles in their classrooms without the solutions being found easily on the Internet.

Please email me at sarah@mathequalslove.net for the password to the answer key database featuring all of my printable puzzles and math worksheets. I frequently have students emailing me for the answer key, so please specify in your email what school you teach at and what subjects you teach. If you do not provide these details, I will not be able to send you the password.

Not a teacher? Go ahead and send me an email as well. Just let me know what you are using the puzzles for. I am continually in awe of how many people are using these puzzles with scouting groups, with senior adults battling dementia, or as fun activities in their workplace. Just give me enough details so I know you are not a student looking for answers to the puzzle that was assigned as their homework!

Sarah Carter teaches high school math in her hometown of Coweta, Oklahoma. She currently teaches AP Precalculus, AP Calculus AB, and Statistics. She is passionate about sharing creative and hands-on teaching ideas with math teachers around the world through her blog, Math = Love.

Similar Posts

3 Comments

  1. Hi. I love your blog and have been following for years. I would like to incorporate more of these puzzles into my classroom besides the first week of school. I don't think I've seen a blog post about how you actually use them in class. I know you used to have the puzzle table but when could students work on them? I don't really have extra space in my classroom and I feel like there is never any down time, but I think that my students would love these and it would really help them exercise their brains. Would you be willing to elaborate on how and when you let students work on these puzzles?

  2. Hi Sarah, I know you don't post puzzle answers, but would you be able to tell me if this problem is possible to solve? I need to know whether it is possible before I give the problem to my students to solve. It's frustrating if they tried for over an hour and the answer is impossible. I don't want to buy the book, it's way to expensive. Thank you.

Comments are closed.