Real Number System Nesting Boxes

I’m excited to show off my real number system nesting boxes to you today.

I hope everybody is having a fabulous Monday!  I’ve really been enjoying my last Monday of summer.  And tomorrow, I will celebrate my last day of summer.  Teachers report on Wednesday for inservice, and we will have students in our classrooms on Thursday!  I’m still not quite sure where this summer went.  Oh wait, yes I do.  This summer was spent going to 16 days of conferences, directing Vacation Bible School, taking a group of 3rd-6th graders to church camp, spending time with family, watching way too many episodes of Doc Martin on Hulu, and reading as much as possible.

Today, I was very blessed to meet some of my tweeps in person!  I had a lovely lunch with @druinok, @Johnsonmath, and @RebeckahMozdeh.  We had some great conversations over delicious Mexican food.  It was good to put an actual person to the twitter avatars that I am used to communicating with. 🙂  

Real Number System Nesting Boxes

Today’s project is something that I actually started way back in May.  Inspired by this pin, I sat out to create my own set of real number system nesting boxes.  Luckily for me, my parents run a business that does a lot of shipping.  They have an entire room upstairs that is full of empty cardboard boxes.  So, with only a little digging, I was able to find the perfect set of boxes.  I used a box knife to cut the flaps off each box, and I cut down each box so that it was the same height.

The green box represents the real numbers. The blue box represents rational numbers. Purple is irrational numbers. Red is integers. Yellow represents whole numbers. Finally, white represents the natural numbers.

This was the part of the project that I did in May.  I retrieved colored paper from the storage room at school to cover the boxes, but the boxes remained uncovered until yesterday.  My sister used some of her art major skills to help me figure out how to successfully cover the boxes.  They’re not perfect, but I still love them.  And I think they will help some of my more visual students realize that because the natural numbers box sits in the whole numbers box that means that every natural number is a whole number.

I actually have one more step to complete before these are finished.  I need to label them!  For some strange reason, I just discovered that I don’t actually have a Sharpie in my house.  My search resulted in a grand total of one permanent marker.  But, it was one of those super jumbo markers, and I decided that wouldn’t be the best idea.  So, tomorrow, I will label each box with the subset of the real number system that it represents!

(Or – maybe I should put the labels on velcro.  Then, students could practice velcroing (is that even a word???) the correct name to the correct box.  And, I could provide laminated numbers that students would have to put in the most specific subset of the real number system.  Hmm…)

A Lesson Using the Real Number System Nesting Boxes

The following is from a blog post I wrote in 2015 about using the real number system nesting boxes with my Algebra 2 students. This was our first skill of the year.

I took some Dollar Tree neon index cards and chopped them in half.  Each card was labeled with a number to sort.

Fun colors make everything better.

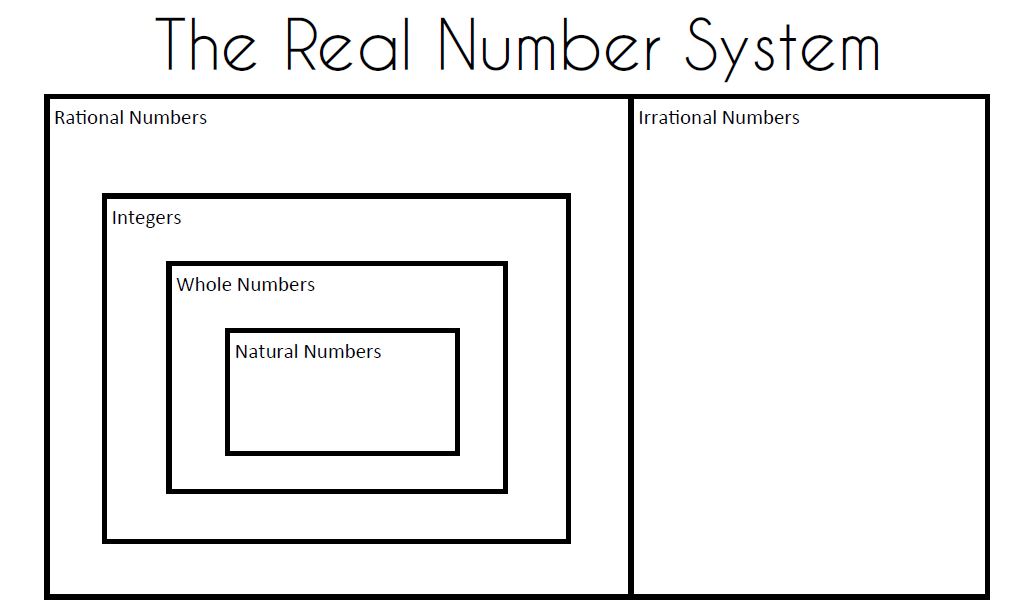
We glued this real number system graphic organizer in our notebooks.  Then, I had the students write the definitions for rational and irrational numbers.  I gave them a quick introduction to the graphing calculator so they could type various numbers in to see what kind of decimal they produced.  We typed in pi.  We typed in e.  We typed in 2/3.  We typed in Radical 2.

A few minutes before class started, I had decided to let each student pick a sticker as they walked in the room.  I used a box of random name badge stickers that have been in my cabinet for ages.  Not sure exactly how I acquired these…

I wrote out a set for each of my Algebra 2 classes.

I made it so half were rational and half were irrational, but I didn’t tell them that. 😉

It turns out that the stickers weren’t that sticky, and they didn’t stay on that well.  One tweep suggested I use paper plates in the future.  I really like that idea!

When kids walked in the door, I fanned out the pile of stickers in front of them and let them choose one.  They just saw the blank backs.  One girl picked the sticker that said pi.  The first words out of her mouth? “Ms. Hagan, I picked your favorite number!”  YES!

After our introduction to the scary looking graphing calculators, I had them type the number off their name badge into their calculator.  Then, I gave them the task of sorting themselves into rationals and irrationals.

In retrospect, I made a mistake here.  I was really just wanting my students to practice using their calculator.  But, now a bunch of my students think that you have to type 2/3 into your calculator to see if it is rational or irrational.  Oops…

I went around the room and had each student read out their number.  The class decided if each student was in the correct category.  If I were going to do this again, I would have everyone sort themselves.  Then, I would do a quick survey and tell the class how many people were in the wrong place.  And, I’d let them discuss to figure it out.  Hind sight really is 20/20.

After we were all sorted correctly, we went back to our seats to finish our notes.

Next, I brought out the nesting boxes.

In 2nd period, I laid them out on the desk like this (but nested).  And, I had students come up, grab a card, and place it in the correct box.  It didn’t work so well.

In 5th period, I handed the cards out to the kids (either 1 or 2) and had them walk up to the boxes and put them in once they had used their notes to classify the number.  SO much better!

Sometimes I feel bad that my morning classes are my guinea pigs since my afternoon classes are all repeats.  Every morning, I learn what not to do when teaching a lesson.

I took the cards out of the box one at a time.  On a blank notebook page, the students listed the number and what subsets it belonged to.  If it was a natural number, I would prompt them with “What box does the natural number box always fit inside?”  Whole numbers.  “What box does the whole number box always fit inside?”  Rationals.  And so on.

Seeing a 3-d representation really helped my students in a way that the 2-d version in their notes didn’t.

We went through all of the numbers.  It was a bit more time consuming than I’d hoped.  If I do this again, I’d want to streamline this section.  Somehow.