Conic Sections Foldables and Graphic Organizers

Today I’m sharing our conic sections foldables and graphic organizers that we glued in our interactive notebooks in Algebra 2.

I’m so sad to be finished with conics.  I just love them that much. Conic cards are a huge reason why I like this unit so much.  My students, on the other hand, are quite glad to be done with conics.  We’ve moved on to sequences and series in Algebra 2, and I have a lot of students who are in love with that chapter.  I’m just excited to see them excited about something!

As always, the unit began with a table of contents.

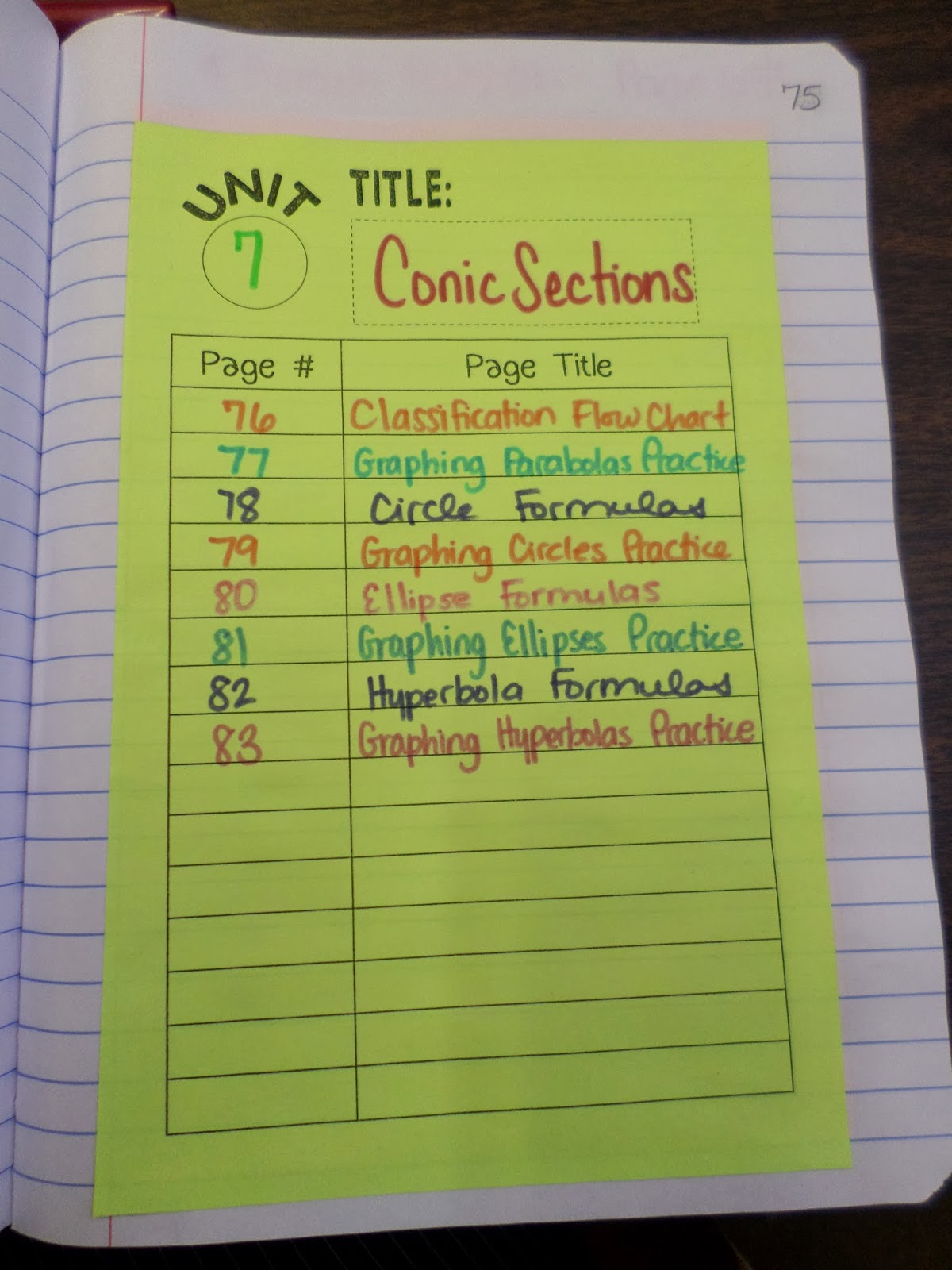
I actually taught parabolas as part of Unit 6 – Quadratic Functions.  So, the page of formulas for parabolas was actually found in the last chapter of their notebooks.  I’m going to go ahead and include that page as if it was in the Conic Sections Unit.

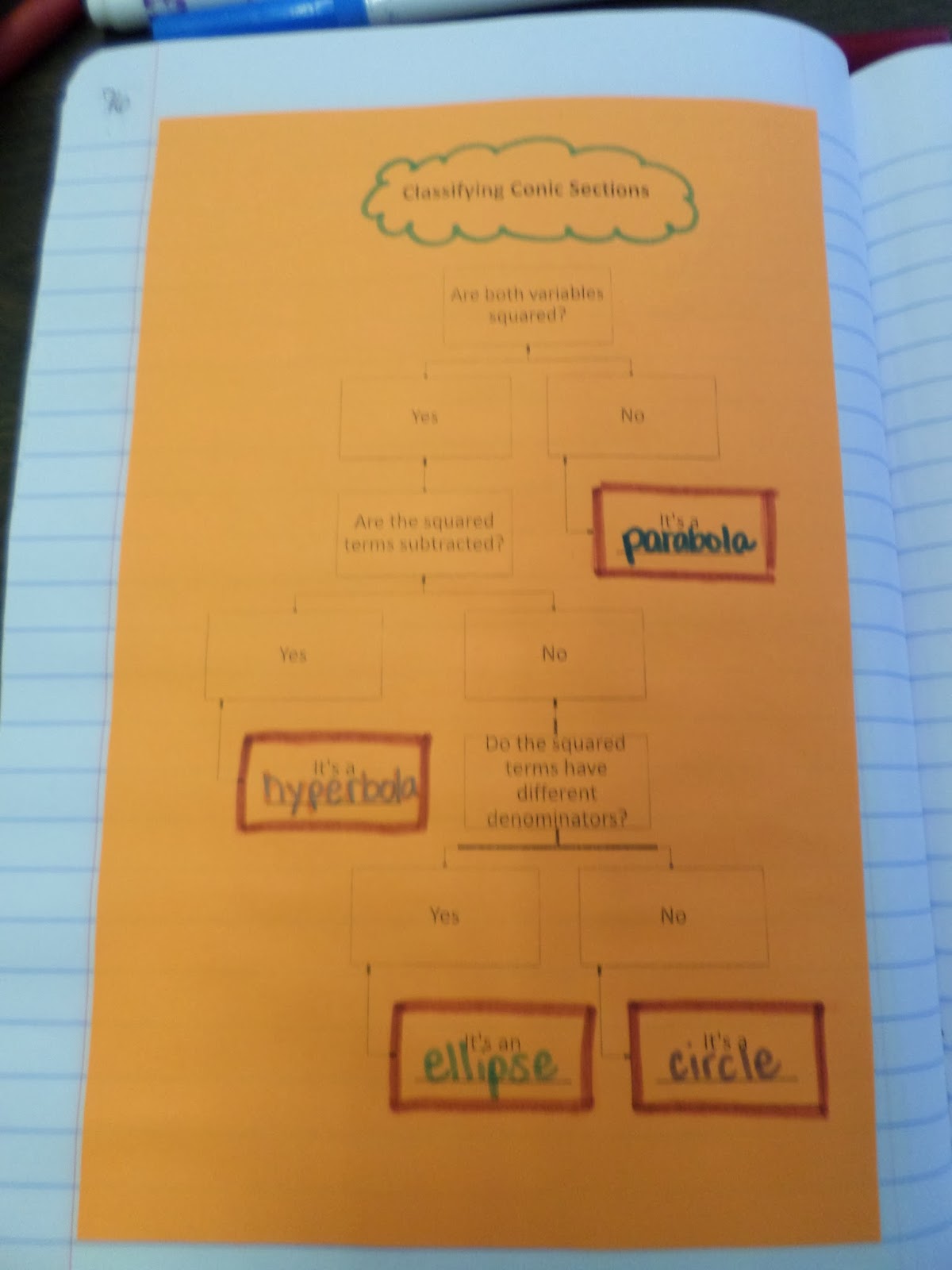
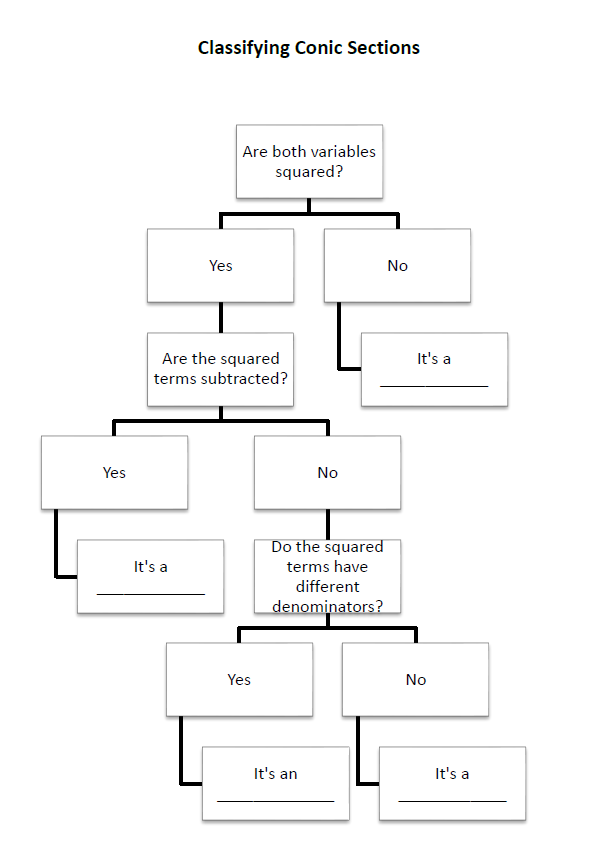
Classifying Conics Flow Chart

I posted about it earlier, but I gave my students a flow chart from Rebecka Peterson to help them identify which conic section corresponded with a given equation.

The formulas and information I gave students were taken from Cindy Johnson’s Conic Cards.  The conic card file contains cards for the students to use that have these formulas on them.  But, I decided I wanted my students to have something in their notebook to reference this year.  I like how these pages turned out, and I’m thinking of doing away with the information cards altogether next year in the conic card decks.  

Parabolas

I love how this student added in extra notes in their notebook.

Next, I made a booklet foldable for my students to practice graphing 9 parabolas in.

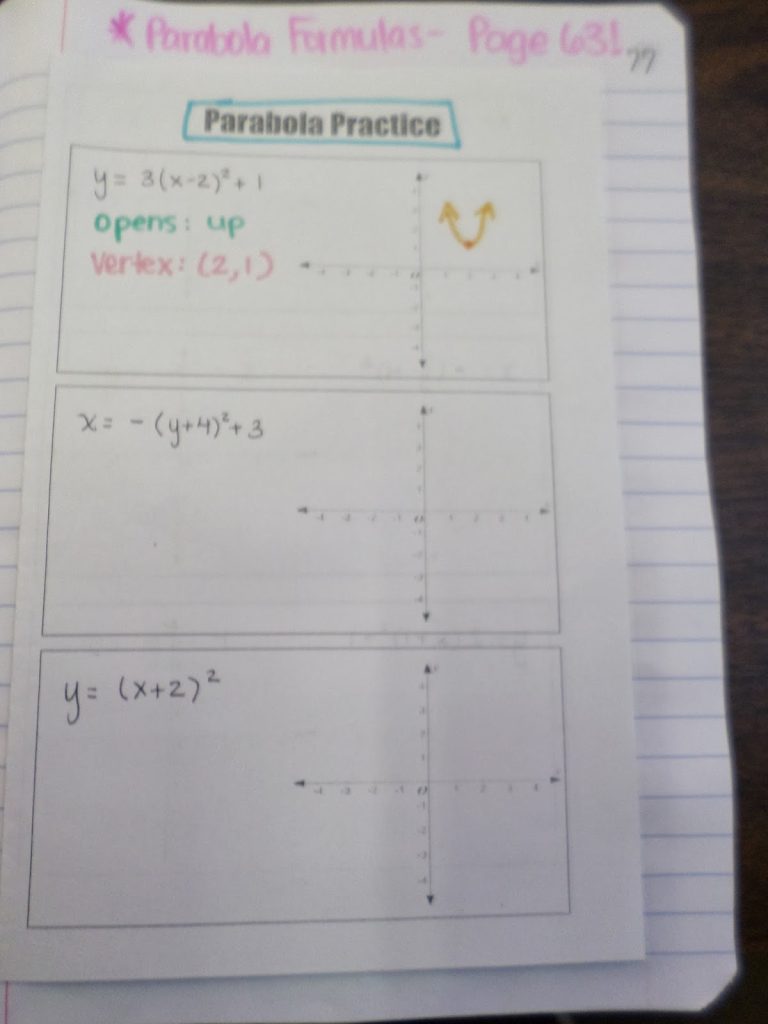
Students had to identify how the parabola opened and the vertex of the parabola.  Then, they sketched the graph.

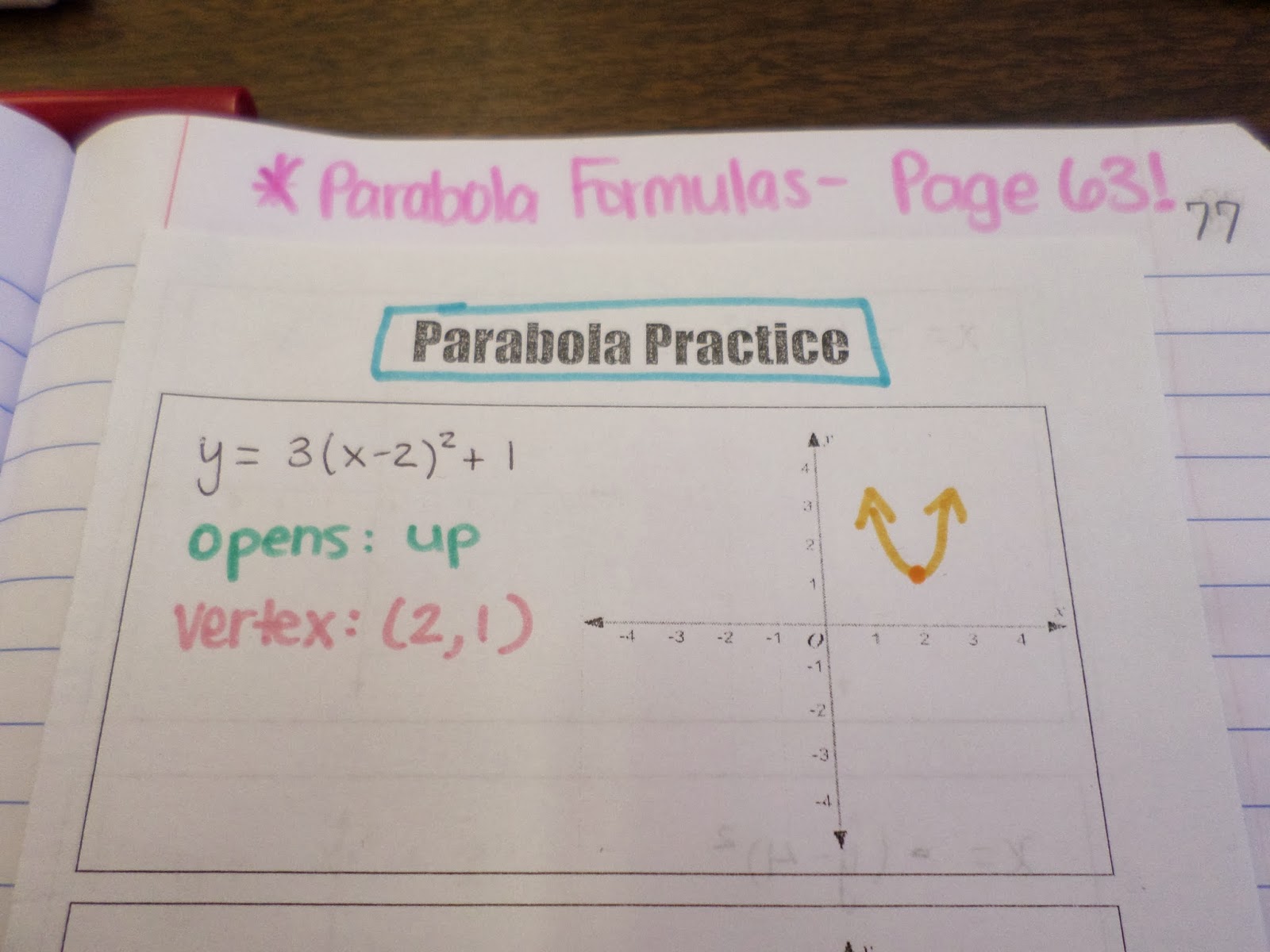
Here’s what the inside of the booklet foldable looked like.  These were graded for accuracy as part of their notebook check.

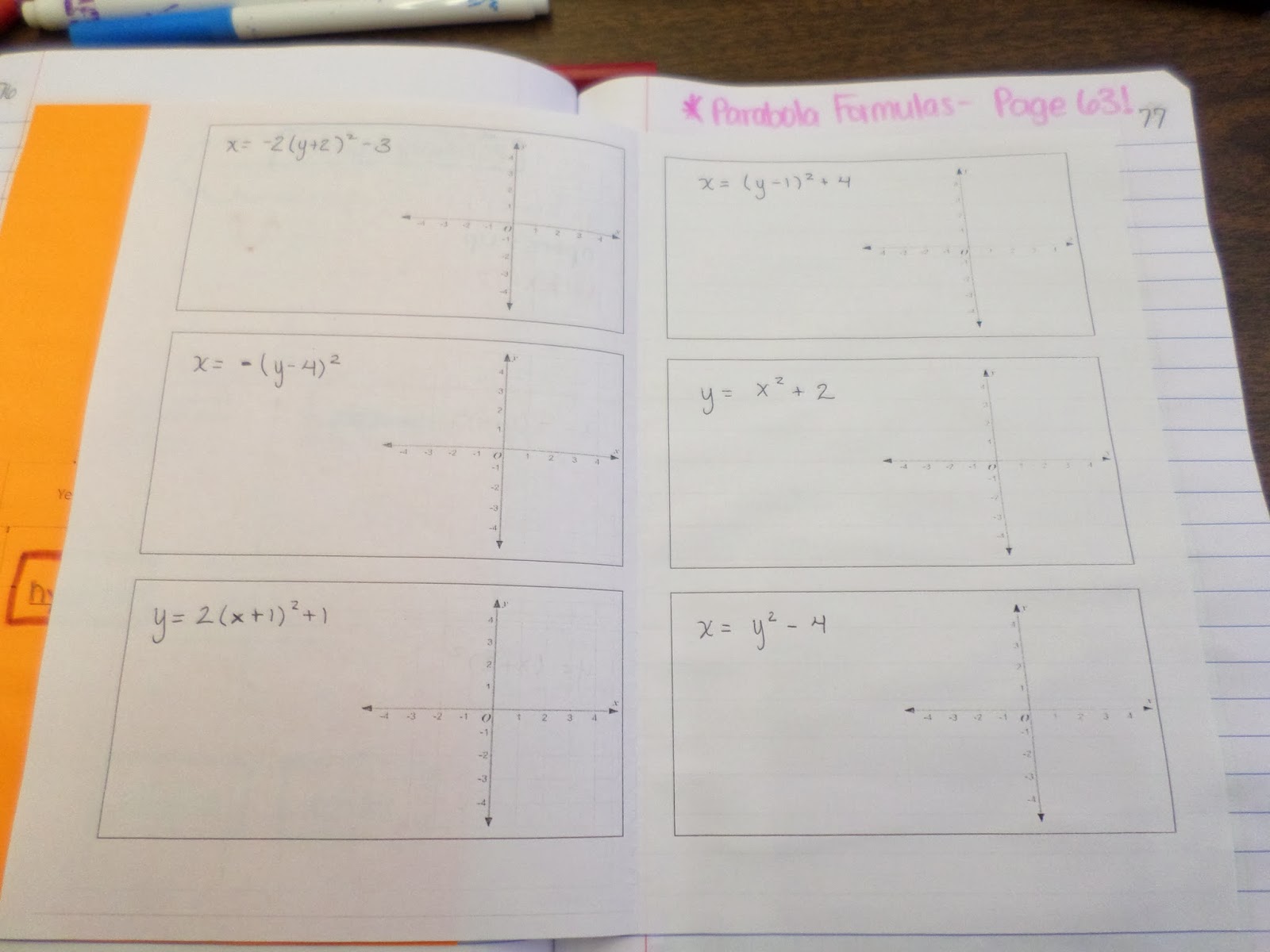
The formulas for the practice problems were not written in, so you could give students any parabola equations that you choose to.

Circles

Next up, circles!  We took notes over the formulas for circles.

And, students got lots of practice graphing circles in their booklet foldable.

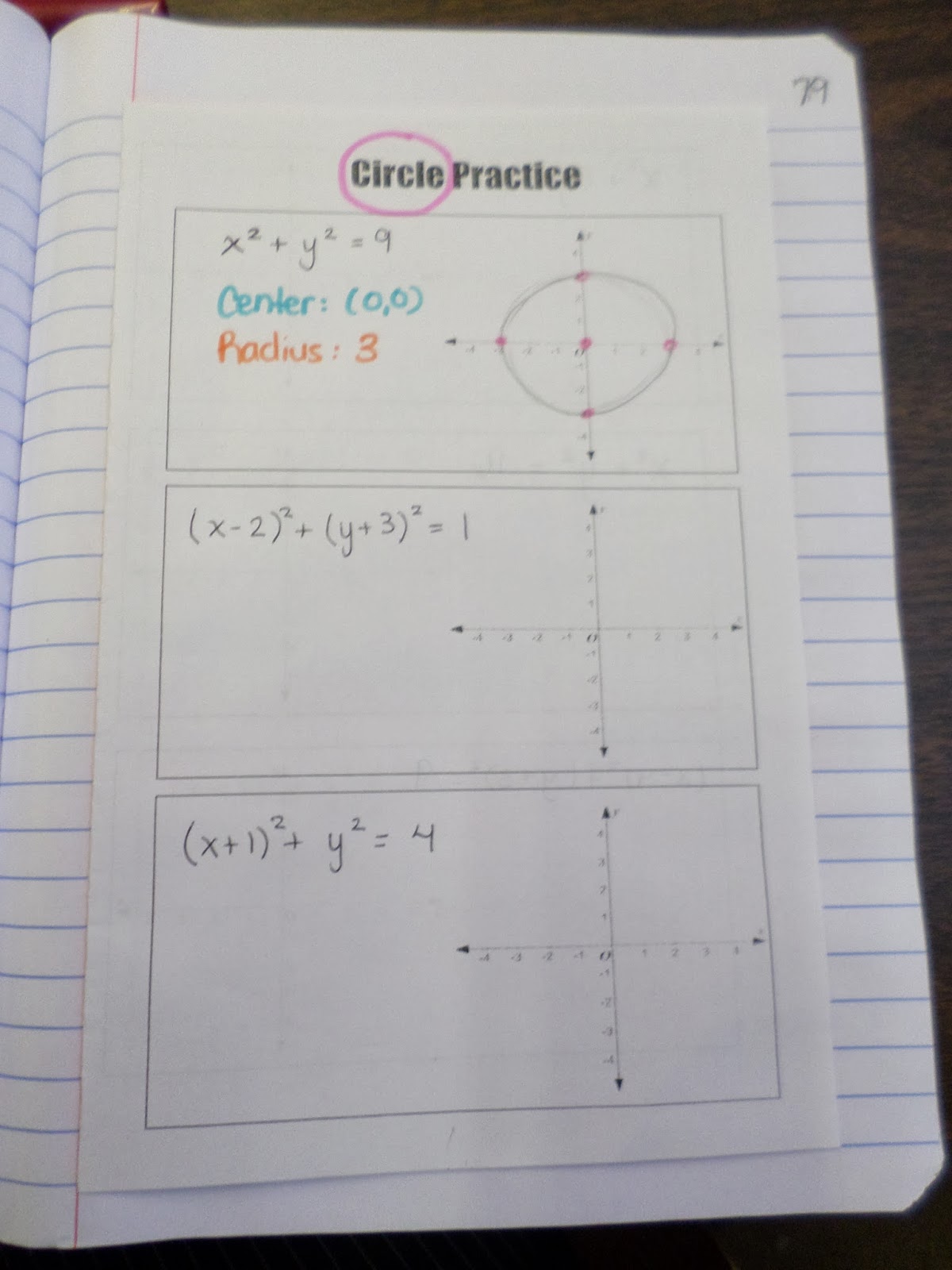
Here’s a close-up of the example circle I graphed with my students.  I really, really, really should have used a compass!  Students were required to identify the center and radius of the circle in addition to graphing the circle.

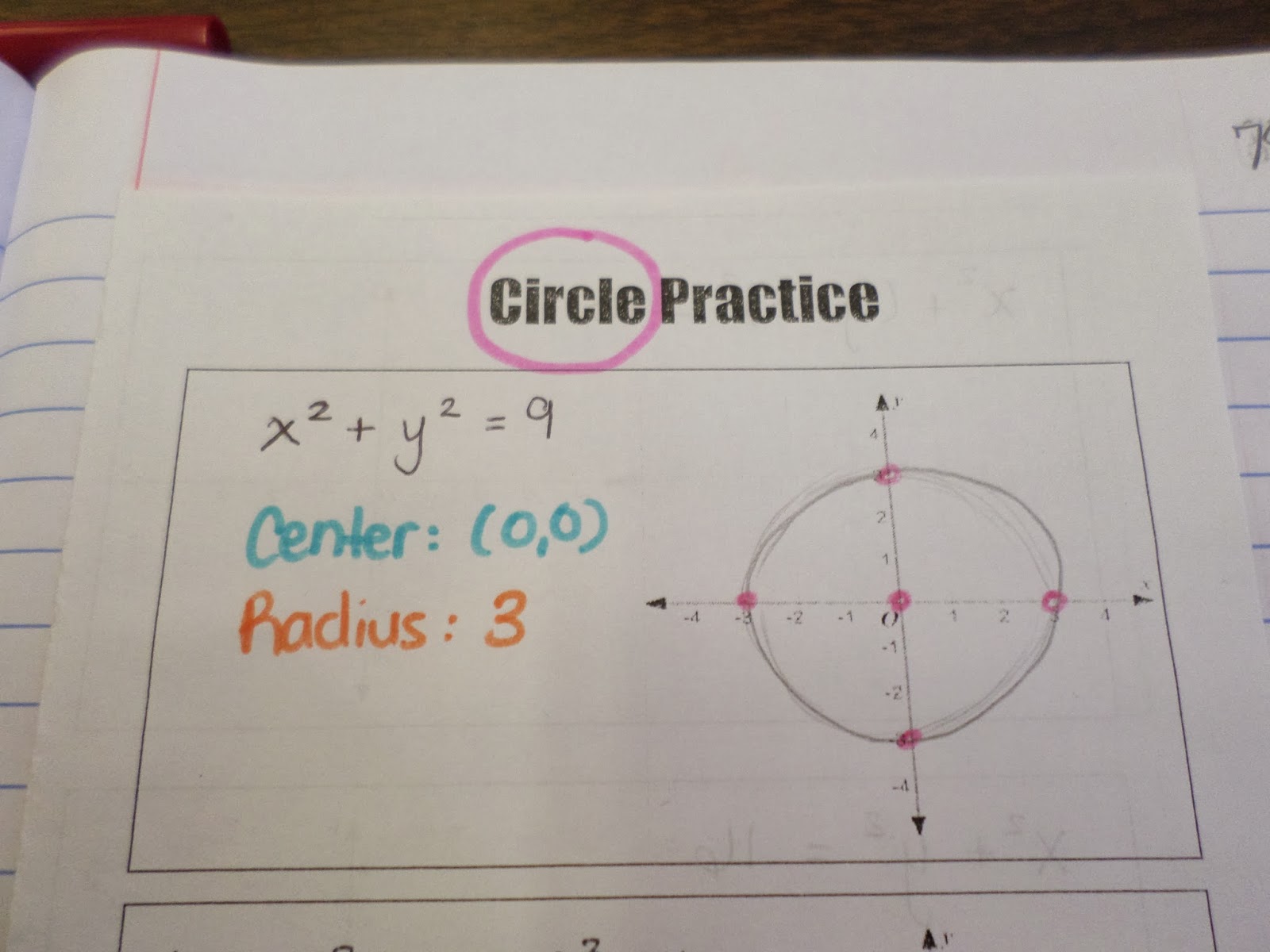
Here are our two pages on circles, side by side.

Ellipses

We explored ellipses next.  As always, we started off by looking at the formulas for ellipses.

We graphed nine different ellipses for lots of practice.

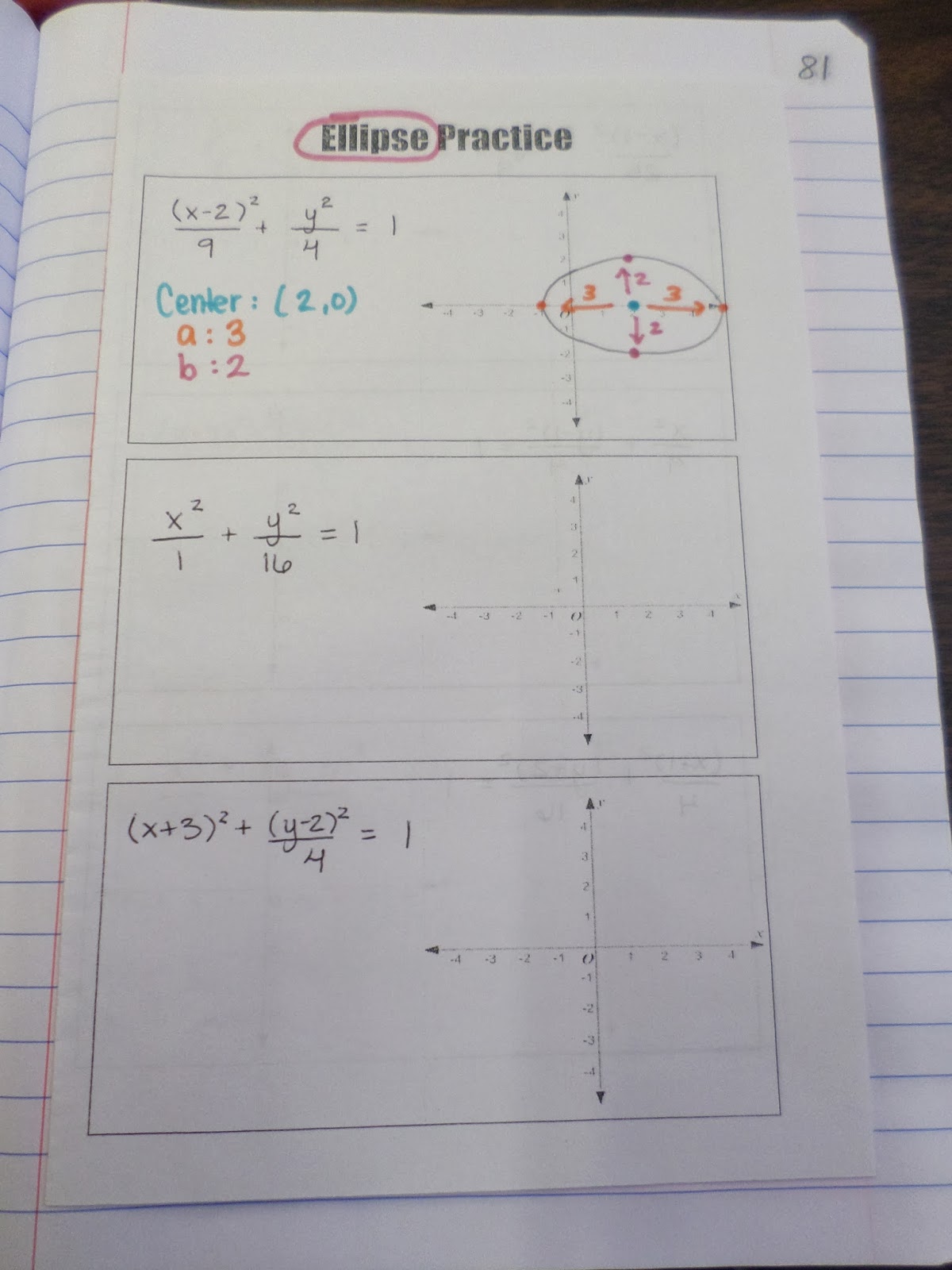
Here are the two ellipse pages, side by side.

And, here’s a close-up that details how I showed students to graph their ellipses.  I tried to employ Color With a Purpose (CWP) here.  I wrote the center in blue and graphed the center in blue.  I wrote the a value in orange and used the orange marker to show how to use the a value to find points on the ellipse.  I did the same thing with the b value.

Hyperbolas

Last, but not least, we explored hyperbolas.  Hyperbolas are my least favorite conic section.  I didn’t want my prejudice against hyperbolas to rub off on my students, so I actually told my students that hyperbolas were my favorite conic section to graph.  I’m not sure how convincing I was, but I did hear some students remark that hyperbolas weren’t as hard to graph as they first imagined them to be.

Here are the formulas for hyperbolas.

There was barely enough information on our Hyperbola Practice booklet foldable to write out the information needed to graph each hyperbola.  But, we made it fit!

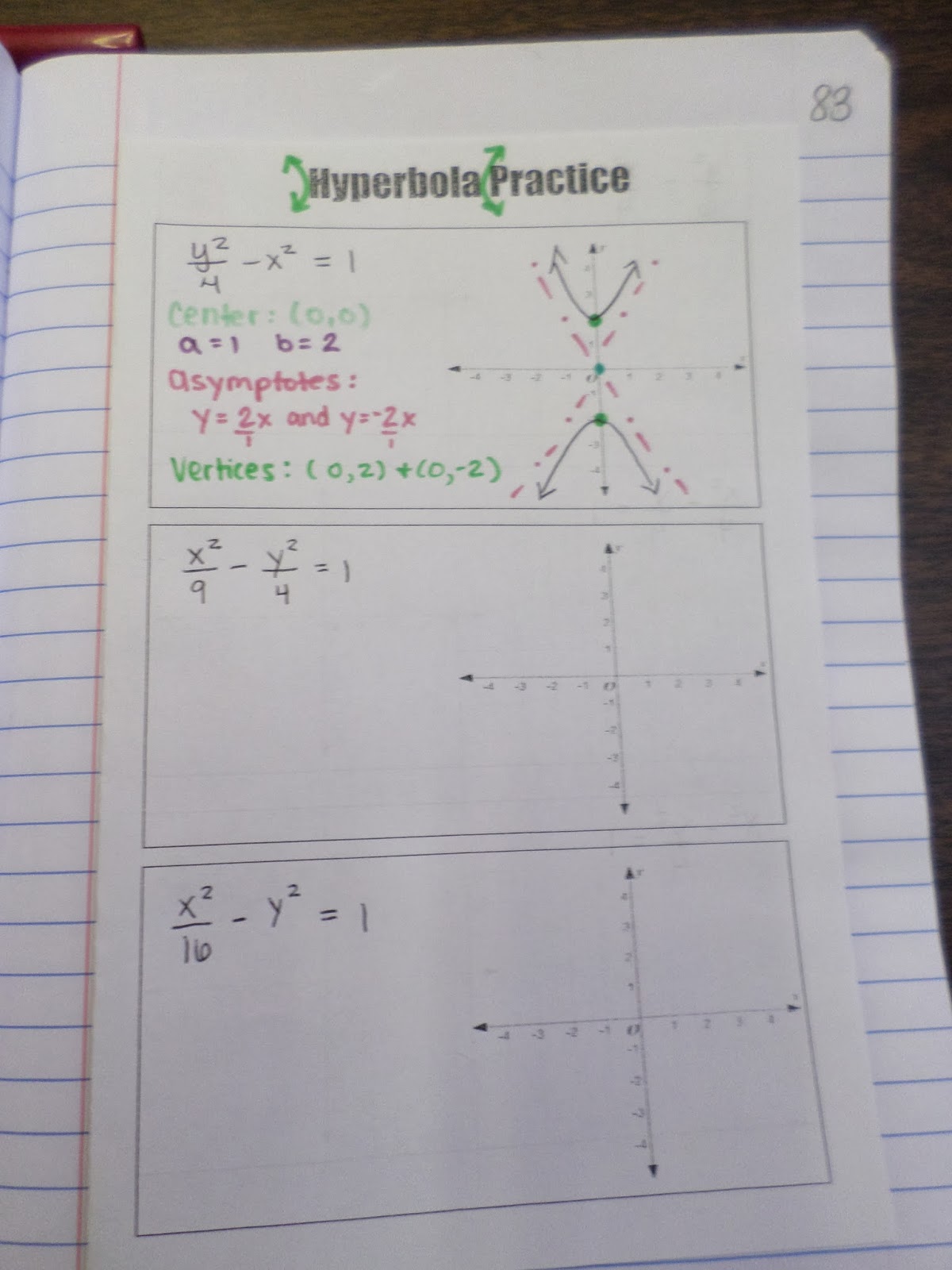
Here’s a close-up of my beautiful hyperbola.  I make my students identify the center, a value, b value, asymptotes, and vertices of each hyperbola before graphing.  I have found that students do a much better job at graphing if they have identified this information beforehand.

Here are the two pages we made for hyperbolas, side by side.