Deriving the Unit Circle Foldable

Several years ago, I created this deriving the unit circle foldable for my trigonometry students to work through and glue in their interactive notebooks. I tweeted about the foldable, but the file never made it to my blog. Today, I am remedying that!

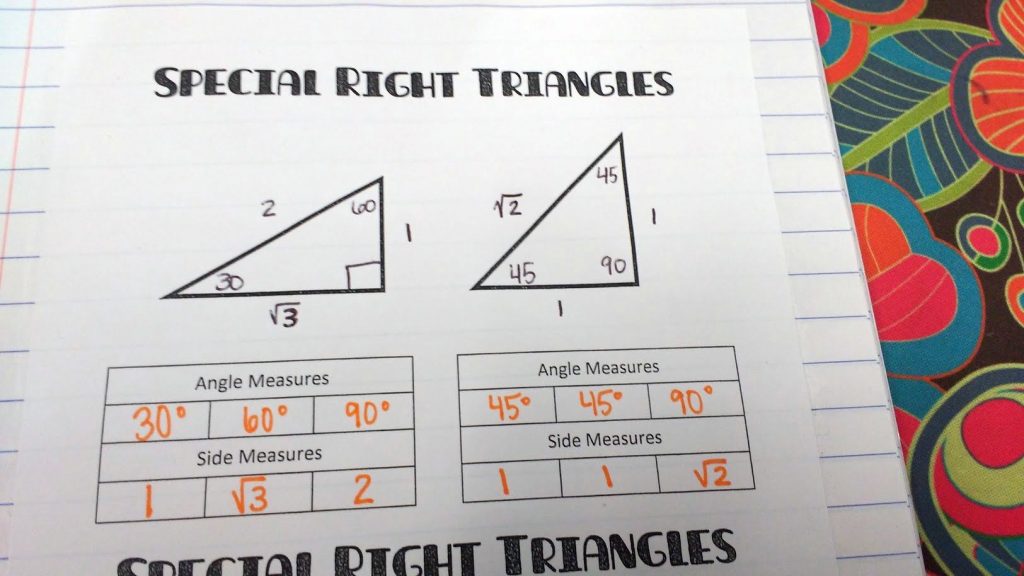
We started with a review of our special right triangles.

First, we went over the special right triangles as you typically see them.

Then, we walked through the process of crafting special right triangles with a hypotenuse of 1 since the unit circle has a radius of 1.

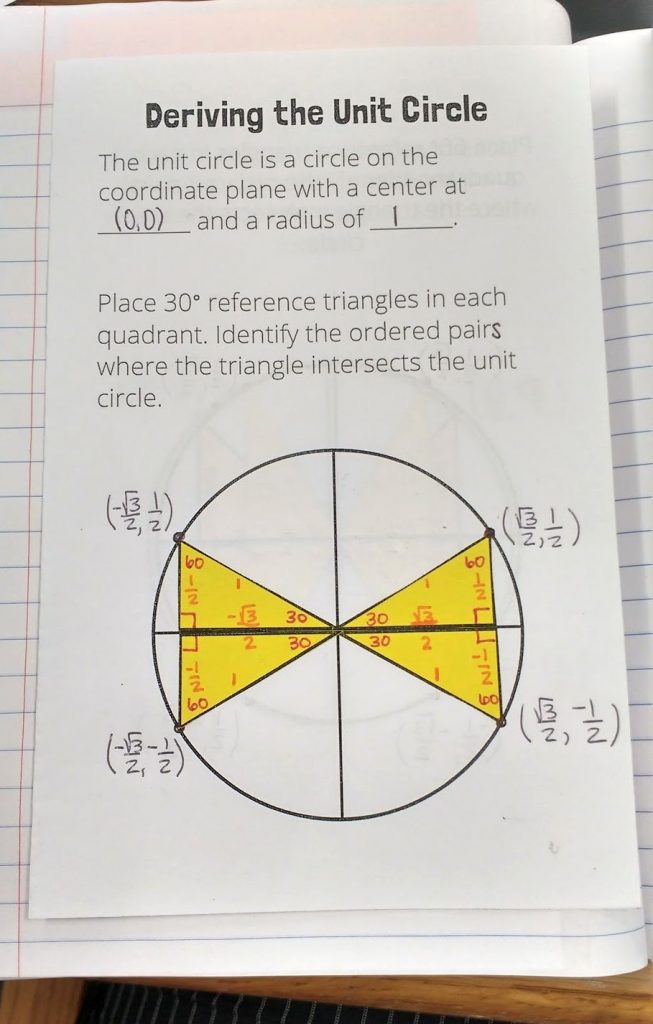
First we, defined the unit circle as a circle on the coordinate plane with a center at (0, 0) and a radius of 1.

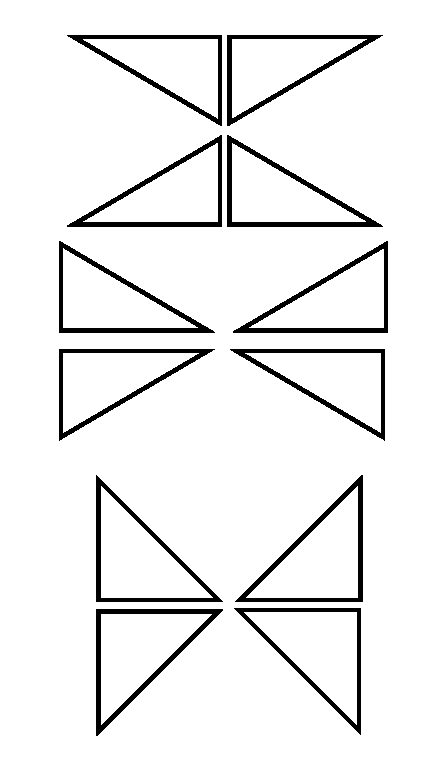
I gave my students a sheet of triangles printed out on colored paper to cut out.

We started by gluing all of the triangles down with a 30 degree reference angle. We wrote in the angles and the sides. Then, we labeled the ordered pairs where the triangle intersected the unit circle.

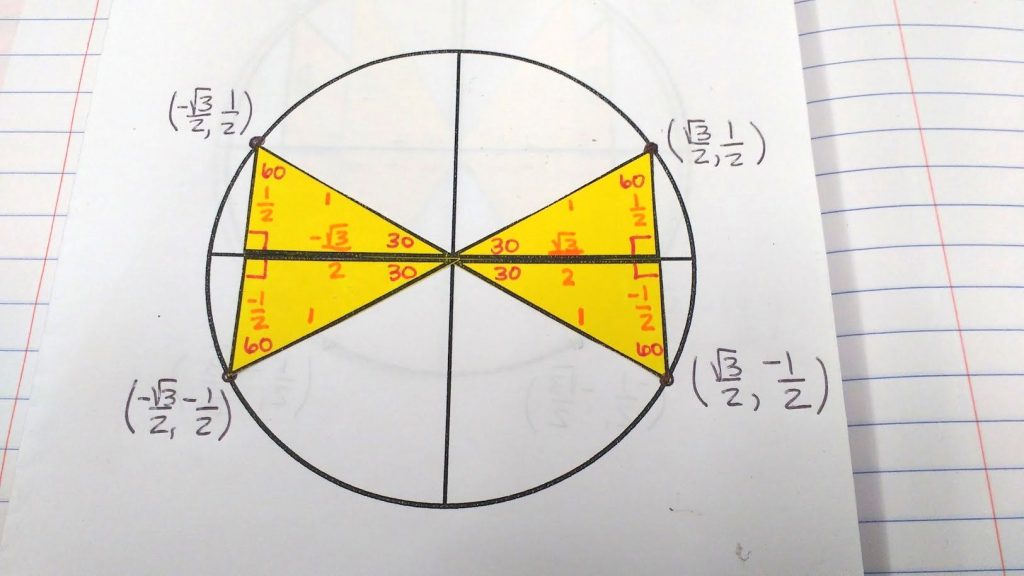
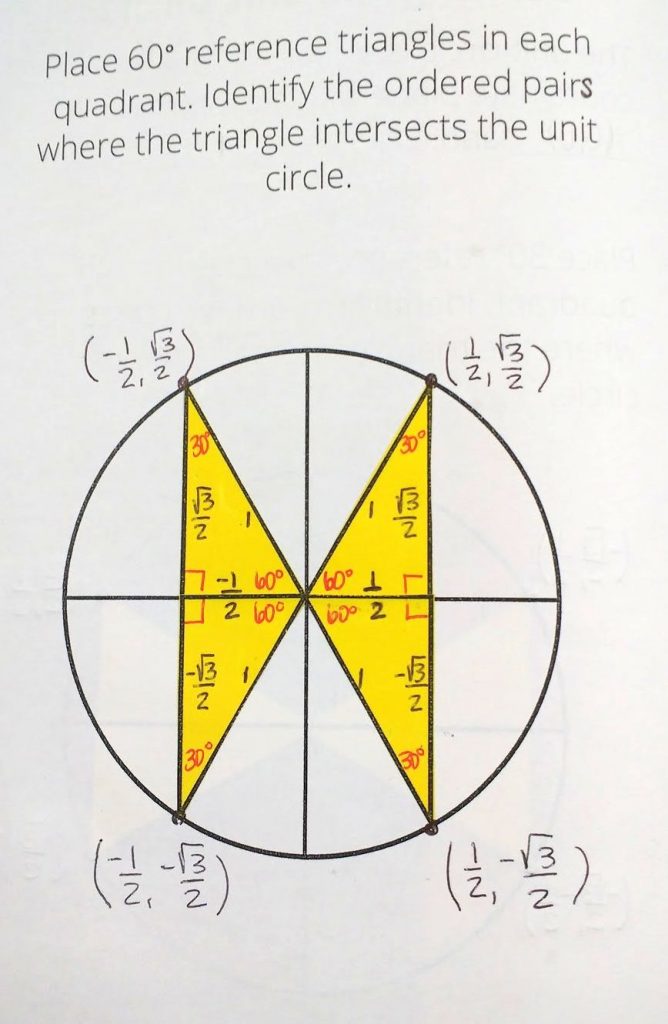
We repeated the process for our 60 degree reference triangles.

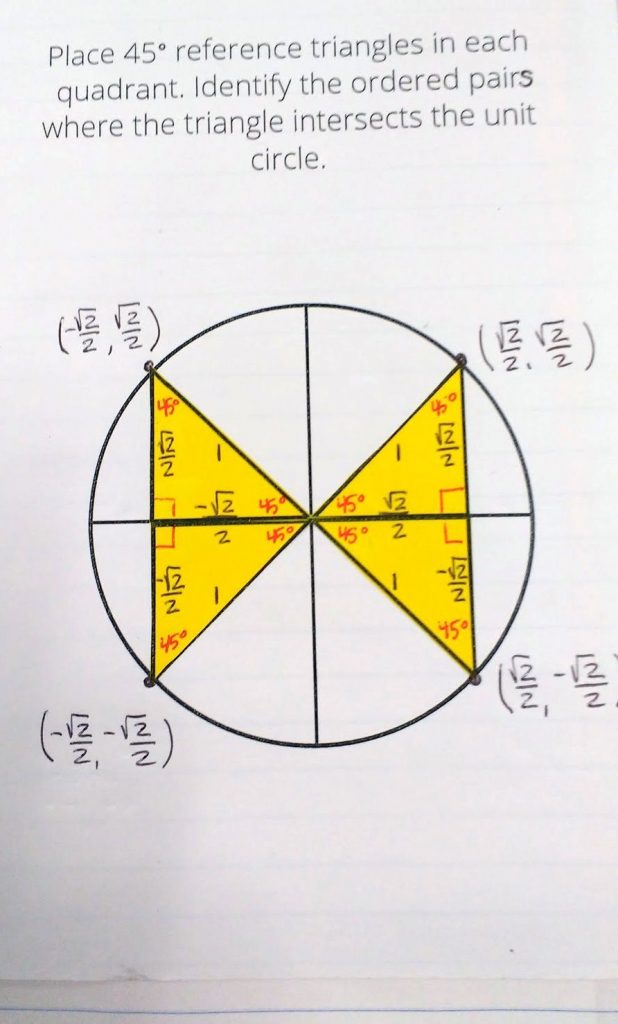
And, finally we did our 45 degree reference triangles.

I wanted my students to understand where these ordered pairs on the unit circle came from.