Factoring out the GCF of a Polynomial Foldable
I’ve always taught factoring out the GCF of a polynomial the way I was taught to do it. And, historically, my students have always struggled with this. I think they usually get the gist of what we’re doing, but they usually struggle with the GREATEST part of GCF.
Last year, I saw Jan Lichtenberger’s post about using the upside down division method to make factoring the GCF (and a host of other concepts as well) easier. It’s like my beloved Birthday Cake Method, but upside down.
Also, if you haven’t checked out the rest of her posts at her Equation Freak blog, you’re missing out. So many great ideas there!
I modified her instructions the tiniest bit to make them fit with what I’d just covered with my students. I gave them this instructions on the outside of a booklet foldable, but they really learned from just walking through the four examples we did as a class.
Seriously. This took less than half of a class period. And my students rocked it.

Even though they didn’t really use the steps, I hope they might reference them if they forget at anytime.
Here are the four practice problems we did together:

Some notes about how this went:
It’s a lot of writing. A lot more writing than the standard way of solving this type of problem. I’m believing more and more that making students write problems out the long way is a good thing. It makes them start thinking about shortcuts. Did you hear that? It makes THEM start thinking about shortcuts. Students thinking in math class is always a good thing.
If you don’t factor out the highest number that goes into each term the first time, it’s not the end of the world. In my example, I factored out a 2 three times. In one class, we actually factored out a four and then a two. In my other class, someone saw right away that we could factor out an 8 and save us some writing. By breaking this down step-by-step, students were actually thinking “Can I factor anything more out?” instead of just getting an answer and thinking they must be done like in the past.
Student also caught on really easily to the fact that all the terms had to have it in common to divide it out. I used to tell them this in the past, but it never really stuck. On the second problem, a student wanted us to factor out a z. A couple of other students chimed in why this couldn’t happen. In that same problem, another student suggested we factor out a five. Again, other students chimed in. I actually didn’t do that much talking in this lesson. It was beautiful.
With the third problem, I wrote it out as taking x out twice. Both my classes realized that we could just take an x squared out and be done with it. Yay!
Then, my students shocked me yet again when they didn’t run away screaming from the last problem. This is usually the type of problem that students just skip without trying which makes me sad. Instead, they walked through it step by step. My first Algebra 2 class of the day took out the x^2, y^2, and z^2 just as I wrote it above. My second Algebra 2 class of the day insisted on us doing it a bit differently. They factored out the 2 first. Then, they asked if they could take the x^2, y^2, and z^2 out ALL at the same time. I tried to talk them out of it. Wouldn’t that be confusing? But, they insisted. And, they did it perfectly. They were so proud of themselves for doing it in two steps instead of the four steps I wanted them to take. What they didn’t know was that the way they solved this problem was almost exactly like how I’d tried to teach students to solve it before and it had gone horribly wrong.
I guess what I like best about this method is that students can stick with it for the rest of their mathematical careers, or they can internalize the process and factor out the GCF without this structure. Either way, kids are doing algebra! I’m starting to think of this method as training wheels without the stigma (hopefully!) of training wheels.
I told my class how my students in the past have struggled with this. They couldn’t believe it. Now, I’m hoping that they’ll be more likely to factor out the GCF before beginning to fact otherwise since they think it’s so easy. Fingers Crossed


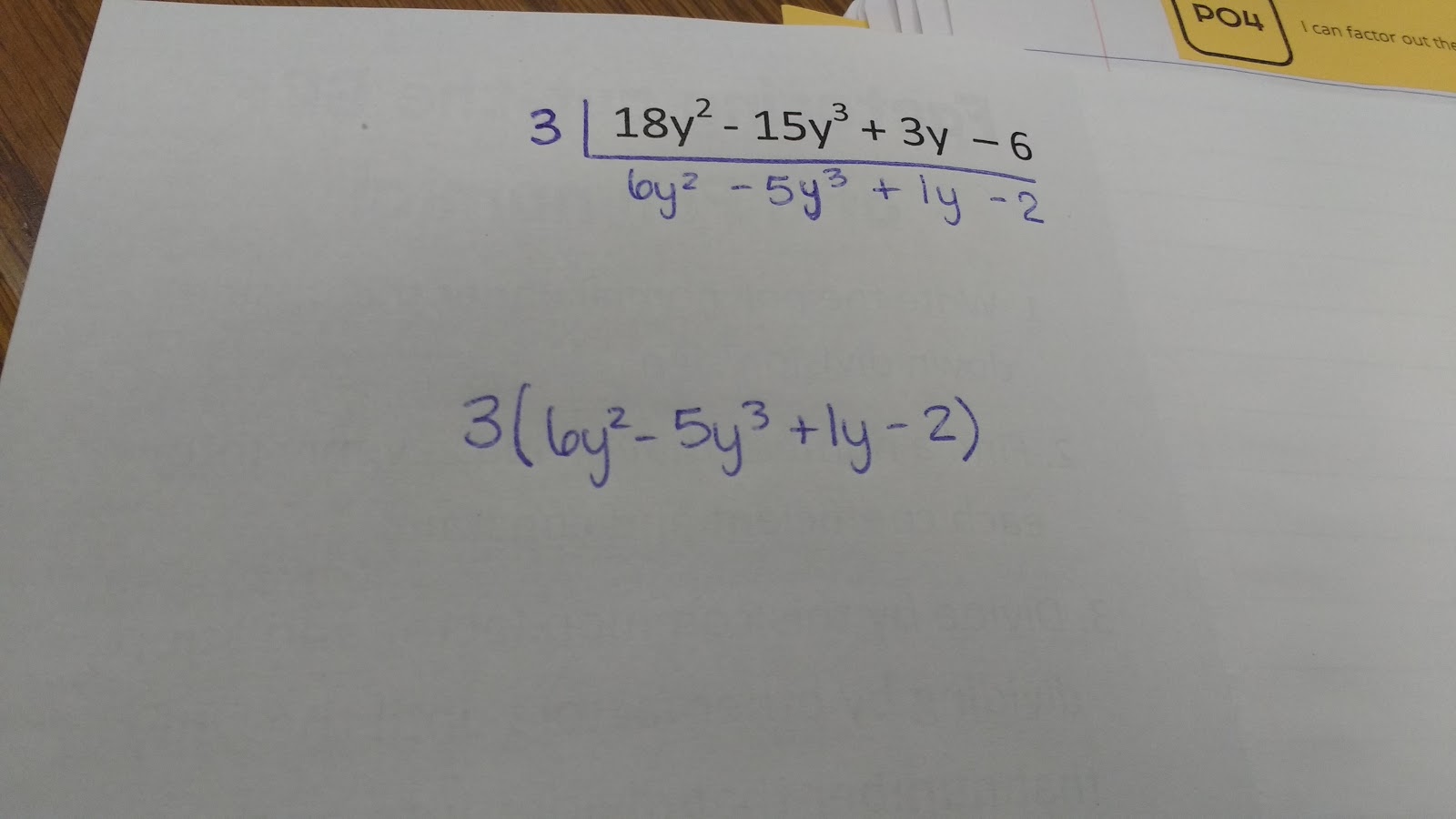
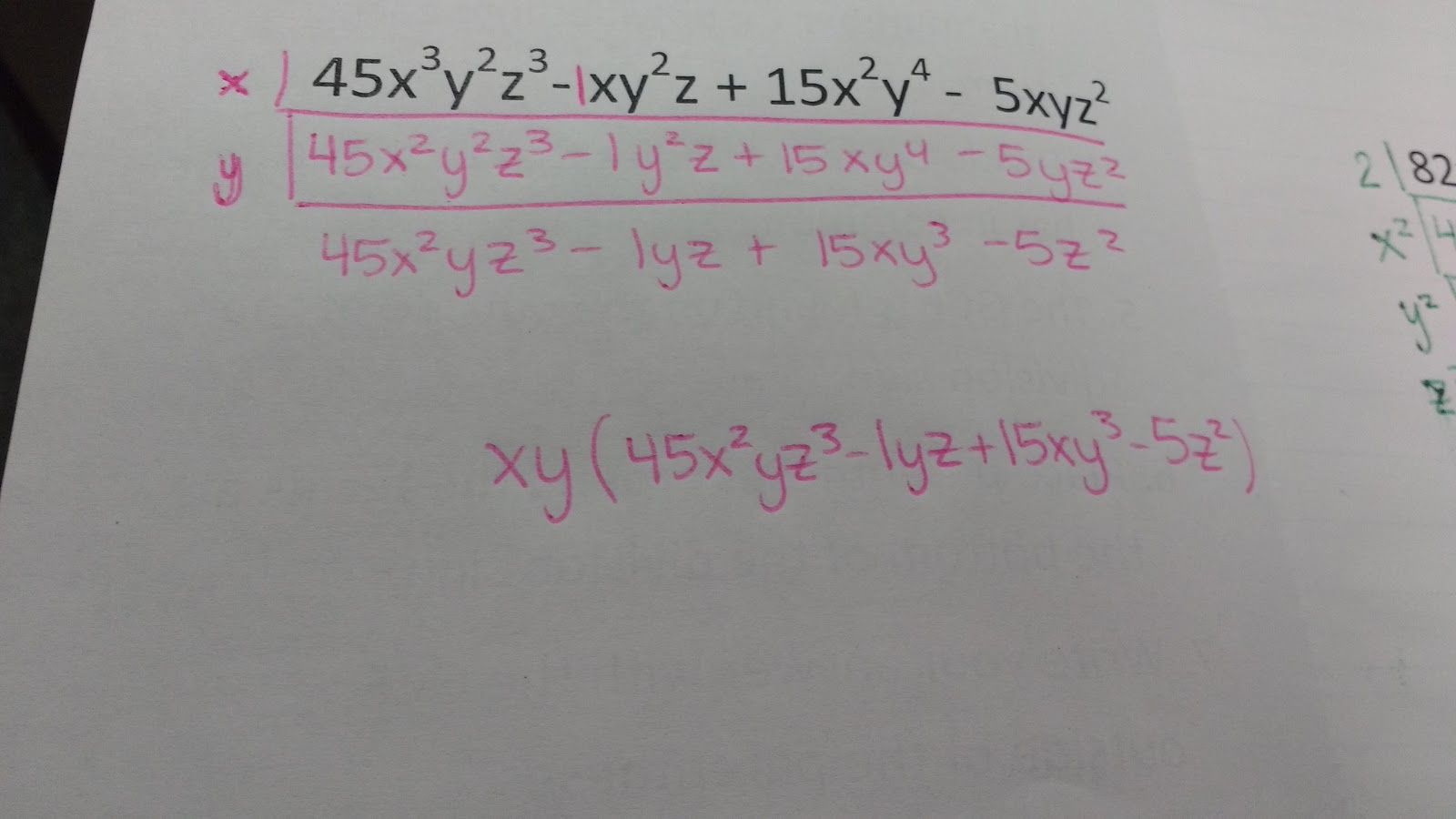
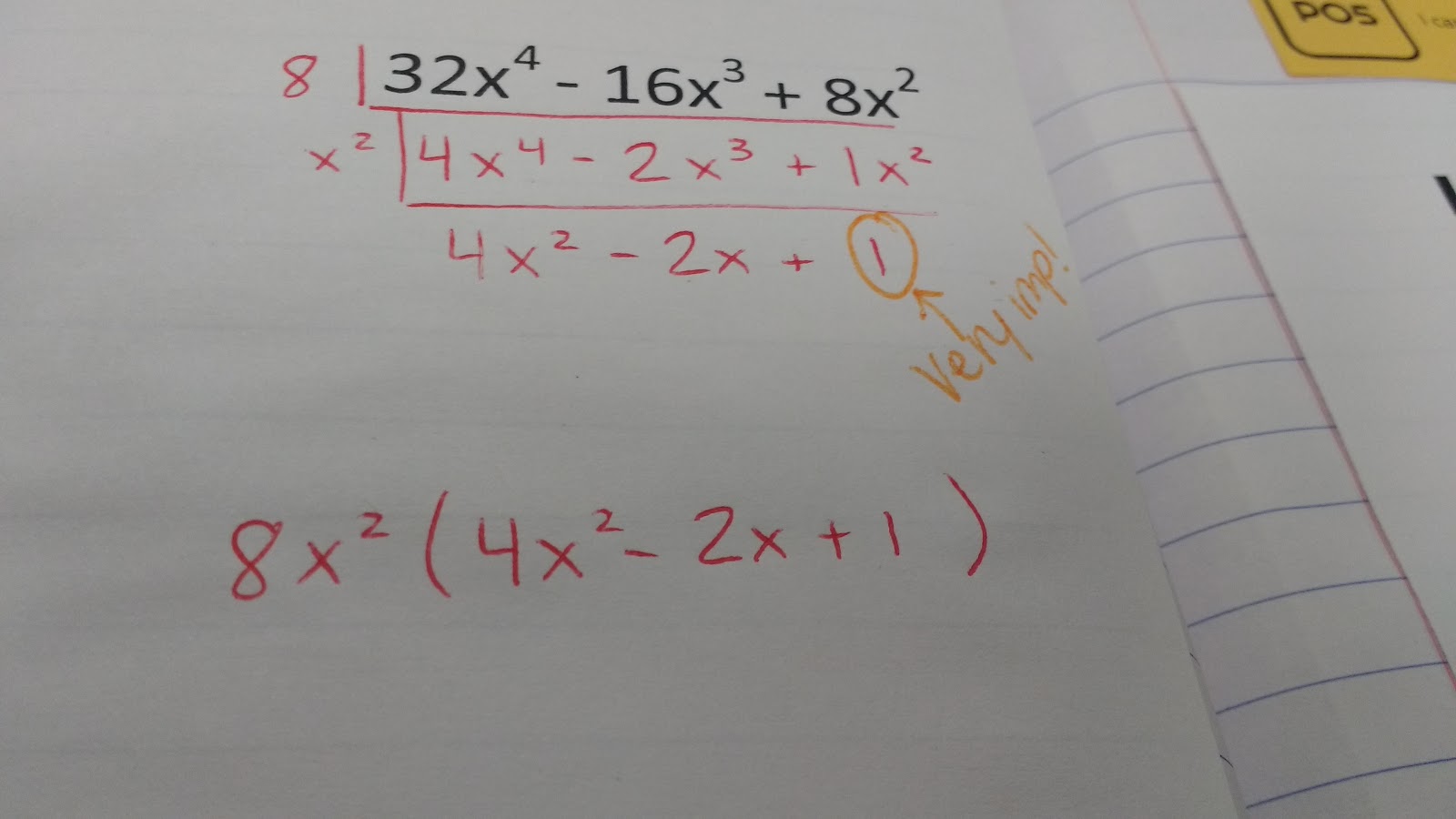
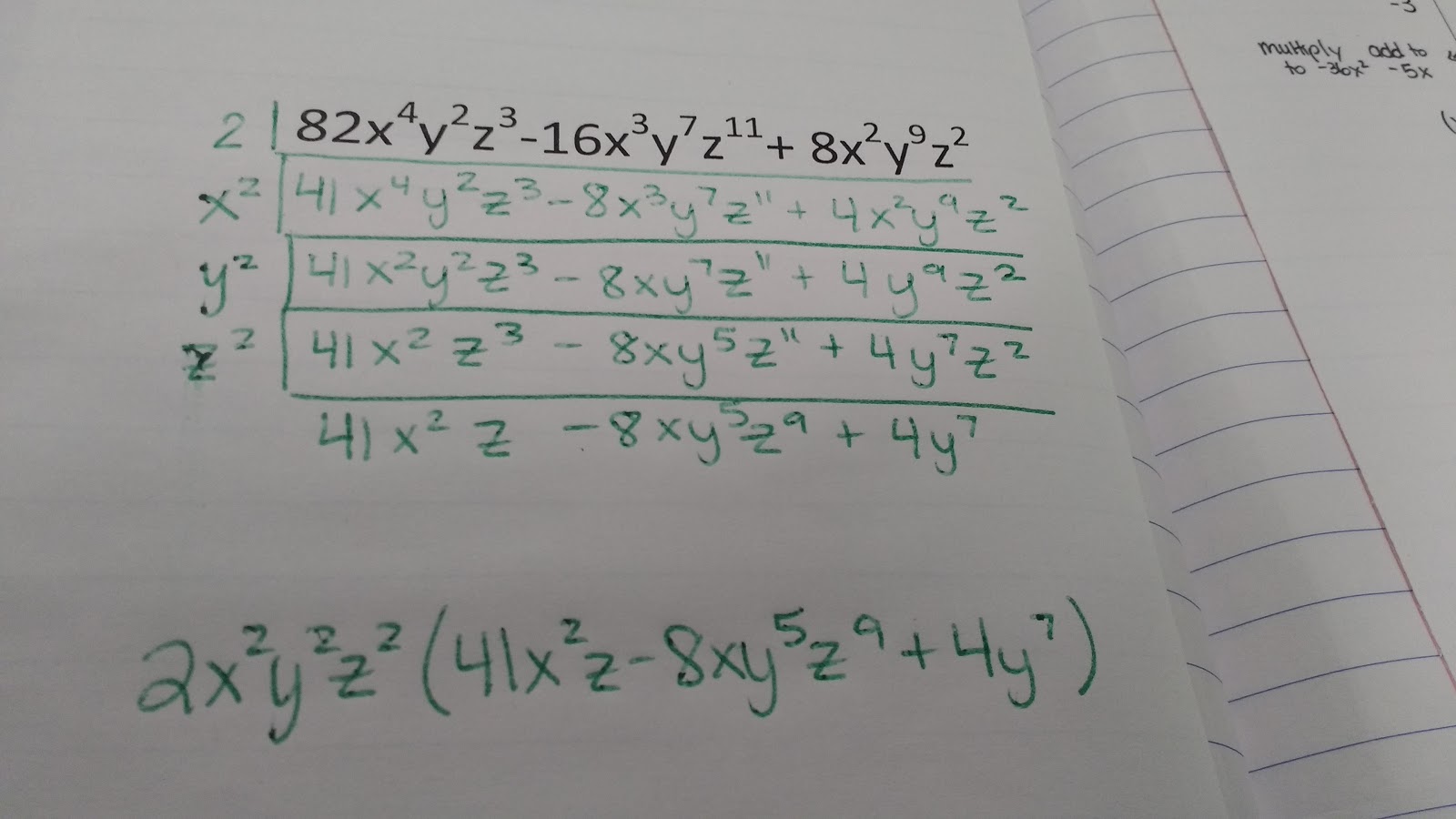
Free Download of Factoring out the GCF of a Polynomial Notes
Click here to Download
Factoring GCF Polynomial Notes (PDF)
1779 downloads – 223.29 KB





This is how I teach this concept, too. Makes more sense than the more traditional method. And you're right – the kids start looking for short cuts. That's always makes me happy!
I think I need to find more ways to have the kids find the shortcuts. I know they'll stick with them longer IF they find them themselves!
Sarah,
You made my day with this post! I'm happy this method worked so well for your kids. My kids find it very easy to understand and I love it when they find the shortcuts too. I'm smiling:)
Seeing kids have such confidence with this usually troublesome topic made my day! Thanks for all that you share!
I used this last week in my sped algebra class. It took a couple days but watching their excitement when they got the correct answer was awesome. Thank you so much for this! Pretty sure I have tried different methods every year but I think this one will stay in the rotation. They loved it!
So happy to read this!
Update – lowest score on the quiz was a 90!!! Doing the happy dance. That NEVER happens. One kid may me grade it right on the spot. When I showed him he was literally bouncing in his seat. Looked at me and said, "I knew I got a hundred". Thrilled.
Yay, yay, yay! Definitely a happy dance moment!
way to much work
Some students need this much structure. If your students can do it in less steps, that is awesome!