Multiplying Radicals Graphic Organizer

30 Comments

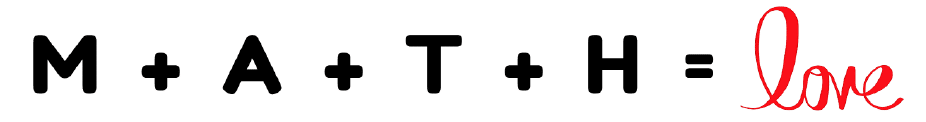
1. I'm enjoying all of your Thanksgiving blogging! I'd love to hear how the SBG experiment goes. Also, how do you grade homework/do you grade homework? My school is moving toward homework being just 10-20% of a student's grade and assessments are 80-90% so that they aren't passing if they haven't mastered the concepts.

   1. Some of my kids love the SBG. Others hate it. I'm loving it, I think. I'm still grading homework. Cheating/Copying homework is becoming a common occurence, though. And, it's frustrating me. I'm thinking of maybe stopping grading homework and only grading quizzes??? I just don't know.

   2. We only grade quizzes and exams where I am at due to cheating being a huge problem on homework. In fact I very rarely assign homework anymore due the huge amount of those not doing it – it was a nightmare for all of us. That doesn't mean I don't have extra practice sheets available for this that want them, I just let the kids choose to do them.

      Btw, I LOVE your blog and have shared it with everyone I talk to! As a first year teacher, it has been a life saver for me!!!

   3. I do not grade homework either. Instead, I treat unfinished homework as a behavioral consequence, ie. detention. We have the option of giving lunch detentions which has been very effective. The lunch detention accomplishes two things: a behavioral consequence and also time for them to correct the behavior, ie. finish the homework!

   4. Thanks for sharing your approach!

2. I'm a lurker and love your blog – sometimes I wonder if we are the same person. We started teaching at the same time, are doing interactive notebooks, and now…trying standards based grading! I also changed because of my unit on factoring. I'm using a 5-10 scale so that the grades in the gradebook pretty accurately reflect their understanding. Mine are also hating that I will give them a 9 for making one mistake. After doing a retest on factoring I think it definitely helped many students. Your blog is such an inspiration! I'm wanting to start blogging soon, in all that extra time we have =).

   1. Hey Anna! I just connected this old comment with your new blog! This is too funny! Though, I have to admit that you are WAY more organized than me! 🙂 I'm so glad that you started blogging.

3. Hi! I just stumbled across your blog and am definitely loving it! I'm a second year High School Math teacher as well and I love some of the things you have here (especially some of your INB materials). I also had factoring trinomial woes with my Algebra II class and was searching, SEARCHING for things I can do better, ways I can help them in the future. I actually found your blog though because I was specifically looking for something about simplifying radicals as you have here. My problem though, is with the absolute value portion of simplifying radicals. For instance, the square root of x^2y^5 would be |x|y^2*sqrt(y). It seems like half the texts and sources I come across just ignore or leave out the absolute value part and make the note: "assume all variables are positive". Did you do that in your class as well? I just don't know if I should bother with the absolute value portion. It's another thing they'll have to remember (i.e. use the absolute value only with even indices, not with odd… and only use the absolute value if the exponent on the variable is odd, not even… ugh, what a nightmare!) and I'm not wholly convinced it is all that useful for them in the world of mathematics. Worse still, I've been using square roots on variables with exponents up until this point without doing any absolute value stuff (like in factoring difference of squares binomials). How did you handle it?

   1. This is going to sound terrible. But, I've totally ignored anything to do with absolute value in regards to radicals. I just don't really remember learning in high school when to use the absolute value bars and when not to. Our state test this year is 100% multiple choice. And, they always put absolute value bars in the answers if needed. I do make my kids aware of this fact.

      This is something I need to do a lot more research on! I need to figure out how Common Core is going to handle this. This is a project for me to look into this summer. It's something I need to do a better job of because the absolute value bars do mean something.

   2. Doesn't sound terrible at all! (Half the resources I've found don't bother with the absolute values, so really, why should we?) And if we get really deeply into this, I'm not completely sold on the definition of a square root being the positive root only. If you're solving x^2 = 16, obviously the answer would be 4 or -4. So why don't we just teach from the start that a square root is the positive AND negative root? It would just make so much more sense to say that x^2 and sqrt(x) are inverses instead of x^2 and +/-sqrt(x). Ugh, I'm going to have to have a chat with the higher-ups about this. 😉

   3. I know this is an old post, but: It's because you eventually will use f(x) = y = sqrt(x) as a function, and functions can only have one value as an output. I don't think this fact was made clear to me in my own high school algebra days, and I had to figure it out on my own later on. Also, the inverse of x^2 depends on what the original domain is: if x is restricted to >=0 then the inverse of f(x) = x^2 would be +sqrt(x). And if x is restricted to <=0 then the inverse of f(x) would be -sqrt(x). It's not really both at the same time.

4. This is my first year using INB, so this has been an experience. The more I use them, the more I like and the students are getting enjoying. I would like to know if other people use these as a review before assessment or as an introductory lesson. What are other teachers doing?

   1. I'm glad to hear that you are enjoying interactive notebooks! I've used them both as a review and as an introduction. I think it just depends on you and your own personal teaching style. I think I tend to use mine more as an introduction. I don't use textbooks with my students, so my students need something to reference while working problems. Therefore, we usually do the page as we learn the concept so students will have that to reference.

5. I love your blogs. As a first year teacher I loved going to your blog and brainstorming ideas as well as searching your blog for your ideas! I am truly grateful that you keep it updated and continue to post your ideas. # Avidfollower:) Last year I did an interactive notebook however was not as organized as I would like to be this upcoming year. Hopefully I will have my website up and running by the beginning of the year. Never realized how hard it was to make your own website!

6. I am so excited to steal this! I tried to teach simplifying radicals yesterday and they did NOT get it at all. This looks awesome!!

7. Sarah – I found your blog after hearing your interview on NPR yesterday. I'm a math loving homeschool mom who also shares your love for the Lord Jesus. Your blog (and your teaching enthusiasm) is marvelous! My current 8th grader, also #8 in our family, is finding some algebra concepts a bit of a challenge. Tomorrow we're going to take a break from our usual program (Jacob's Algebra) and begin working through your radical functions unit to help him firm up his ability to work with radicals. Thank you so much for taking the time to write about your creative approach to teaching math. I'm looking forward to reading and learning more from you!

8. I am in love with your blog! I am currently working to create an interactive notebook for my high school SpEd math classroom NEXT school year. Sometimes the challenges we face in the classroom leave me a little perplexed, so I turn to google. Every time I search something I'm stumped on, it leads me back to you and all your creative ideas! Thank you so much for providing all of your resources on the blog and sharing your ideas with the world!!

   1. THANK YOU! You should totally share your notebook creations, too!

9. I found your blog a month or so ago from a teaching friend in Illinois (I'm in Minnesota) and have been looking at different pages almost daily. I usually end up with 4-5 tabs open from links to previous posts of yours and outside resources. THANK YOU for posting the links to everything including old blog posts!! I'm a first year teacher, so I'm always looking for new ideas on curriculum, classroom set up, and classroom management. By finding ideas here, I feel like I'm not pestering my mentor teacher and doing things exactly the same as her.

   1. Let me know if there's ever anything I can help you with! Hope your first year is going well!

10. Thank you for your time and efforts. I am new to using ISNs with my classes. It is a definite work in progress ;). I have made reference to your blog quite often this school term. Are the PDF links on this topic accessible? I am unable to download them.

11. HI! I just found your blog, and it looks great!
    When I teach simplifying radicals, I tell my students that it's just like their dating life: Pairs go out, singles stay in – Usually I start with index 2, and then move on to groups go out. The students always think it's mean to say that, but I think they remember pretty well 🙂

    1. Thanks for sharing!

12. 23 is a prime number.

    1. It definitely is! Thanks for catching my mistake!

13. This is my first year teaching and am doing 8th Math AND Algebra… your blog has literally saved my teaching live! I almost always use your stuff, so BIG thank you for all your hard work!

14. I stumbled upon your Birthday Cake method last year and my kids loved it so much!!!! I've never had a group to understand simplifying radicals so quickly.

    This year I can't wait to use your notes for adding/subtracting/multiplying radicals. These are awesome. Thanks so much!

15. I love your material…but it's hard to get because I have to have a box account
    🙁 Is there any other way to download it?

16. Ok.. I figured it out 🙂 Thank you for all of your great resources!!!!

17. Thank you for all of your wonderful resources! May I add one thing to your radical unit? I stumbled upon a great method for understanding radicals! Take 3 deck of cards and take out all of the composite numbers, leaving only, 2, 3, 5, 7. Group students by 3's or 4's. Designate a dealer and have them shuffle the cards. Deal each student 10-15 cards each. Instruct the students to make pairs and pile the "books" on the side. Talk about how they were chosen and ask about the cards left over. Do this with books of 3's, 4's and 5's. It reinforces the idea of the index and how many you need to get out from under the radical! I am trying it tomorrow.

Comments are closed.