Solving Word Problems with Ratios and Proportions Foldable

Want to know something exciting?  I taught ratios and proportions in Algebra 1 without once mentioning cross multiplying.  Two kids brought it up as an option, but I quickly told them that there was a way to do these problems without cross multiplication.  Now, I learned to cross multiply in middle school and did just fine.  But, my students have become so attached to cross multiplication that they do it all of the time.  Adding fractions?  Let’s cross multiply.  Multiplying fractions?  Let’s cross multiply.  Dividing fractions?  More cross multiplication.  Ugh…

I’ve decided that the secret to having my students set up proportions correctly is to make them write the units on BOTH sides of the proportion.

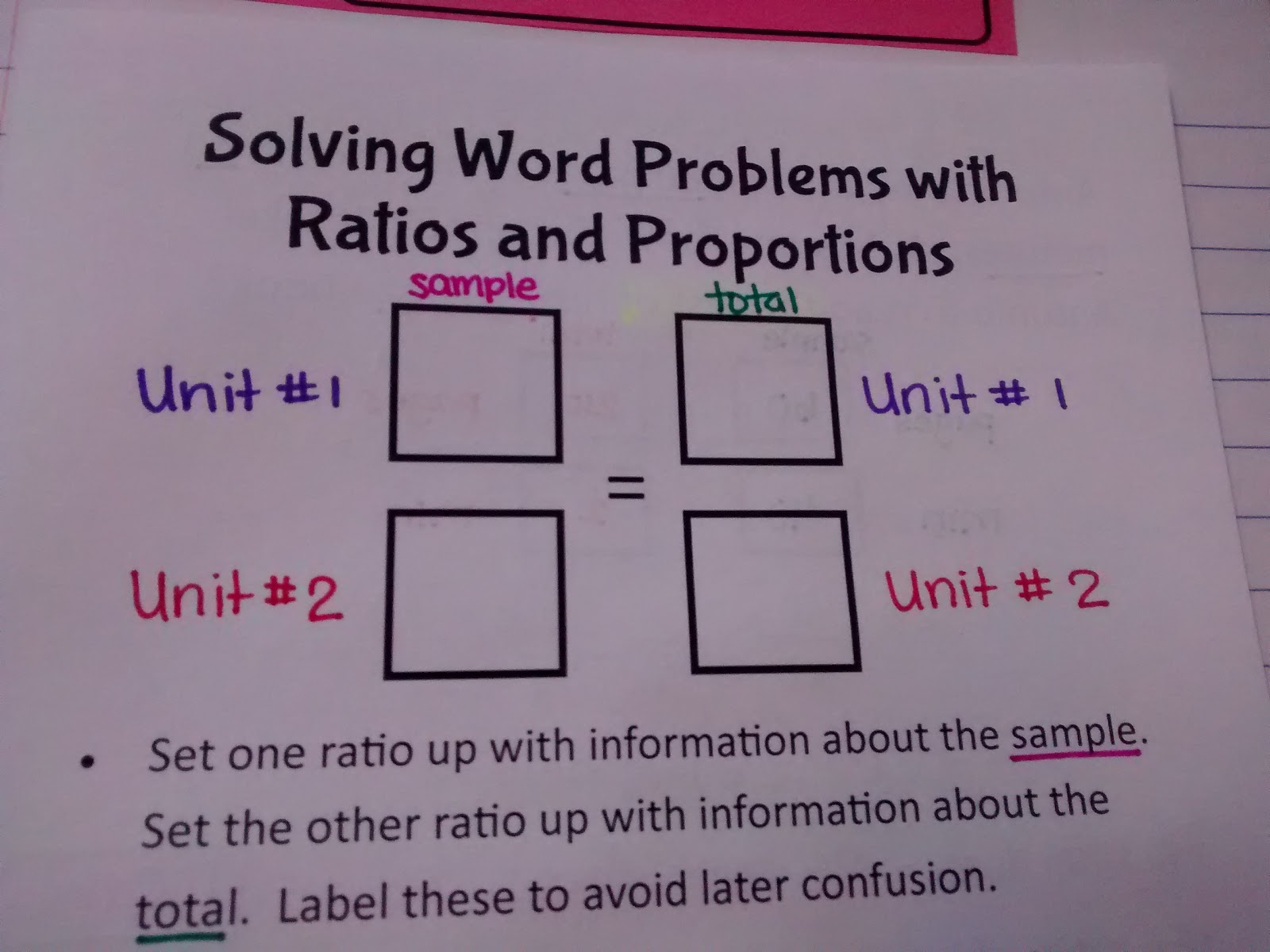
And, to get around cross multiplying, we just take the reciprocal of both sides anytime the variable we are solving for is in the denominator.  Yay for nixing the tricks!  

Here are the 4 practice problems we worked together in class.  The problems are written to mirror the type of questions that may be asked on the end-of-instruction exam.  The past two years, I’ve kinda skipped over this because I believe students should have mastered this type of problem at the middle school level.  But, our middle school math scores have been extremely low for the past several years.  So, I can’t assume that anything was retained from those classes.  I know they’ve retained some things; I just can’t be sure what those things are.

So, this should be largely review for my Algebra 1 students, but I hope it is also helping my students to become more comfortable with word problems which is one of my goals for this year.

Here’s a close-up of the four problems we worked.

My students especially find these problems tricky where they give them the ratio of two types of something and then ask them to find the total number or give them the total number.  On the SMART Board, we started out with 4 boys/5 girls.  We put 90 students/x girls on the other side.  This meant we had to change boys to students and add 4 boys to 5 girls to make students.

After working through this one, most of my students rocked the question like this on the quiz!  In years past, it’s always been one of the trickiest questions for students when we started reviewing for the end-of-instruction exam.

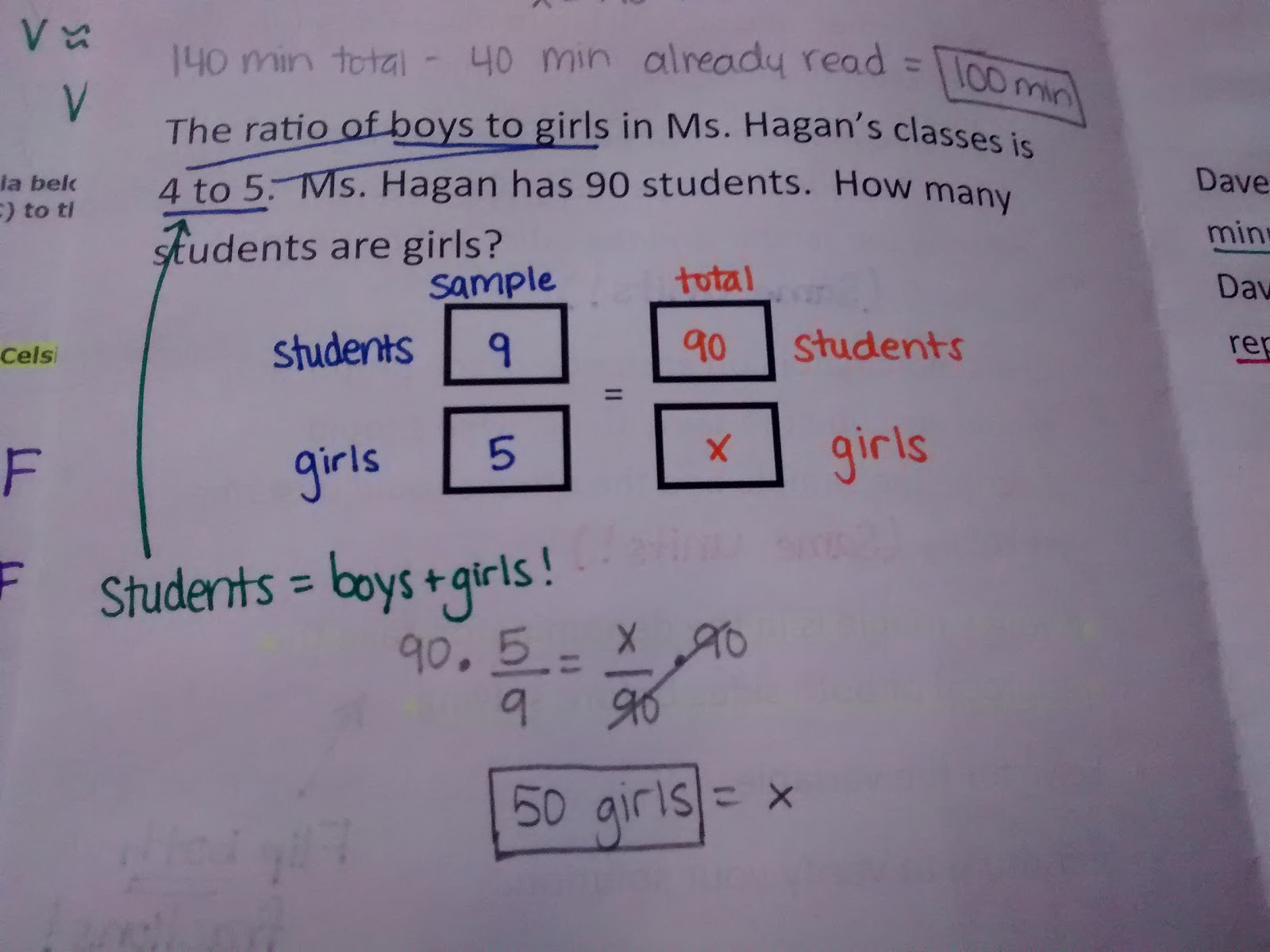
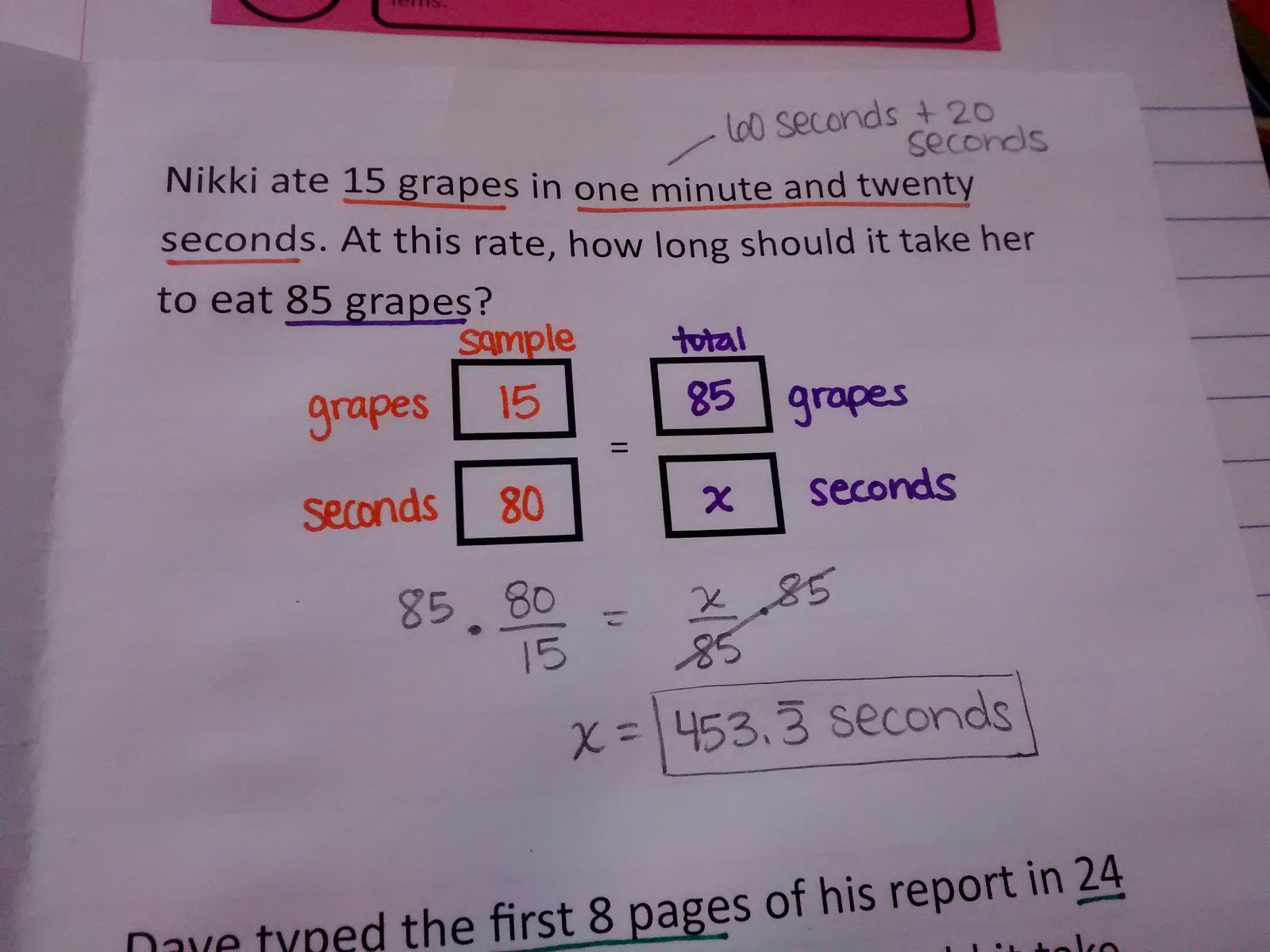
Full disclosure: my students did terribly on this quiz.  But, it was also the last day before Fall Break and a 5-day weekend.  Nobody wanted to be there.  When they came back from Fall Break, we worked through the quiz questions, I reiterated the importance of writing out ALL of our units, and the students re-quizzed the next day with much better results.

In retrospect, I should have just spent Tuesday doing more practice problems instead of making them take the quiz that day.  I had been hoping to wrap up ratios and proportions so we could move on to percents when we got back.