Standard Form of a Linear Equation Foldable
Today I’m sharing a standard form of a linear equation foldable I created for my Algebra 1 classes.
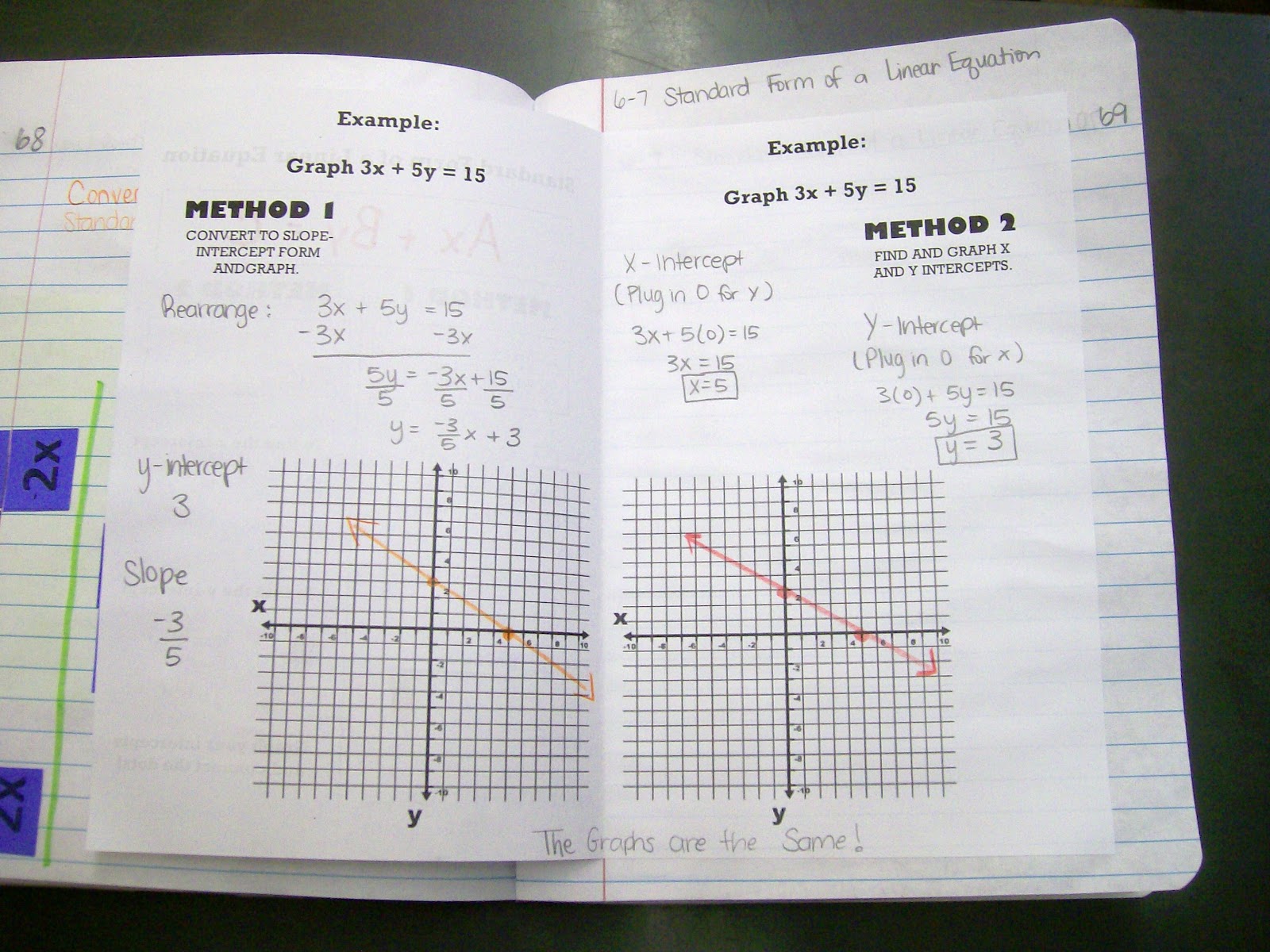
Last week, my Algebra 1 students worked with linear equations in both slope intercept form and standard form. We practiced graphing equations in standard form by converting to slope intercept form and by graphing intercepts. At first, my students did not like graphing intercepts. However, after several problems, that became their method of choice.
I created a foldable to help students organize their notes on standard form. I wanted students to know exactly where to look for the steps in solving and where to find a completed example.
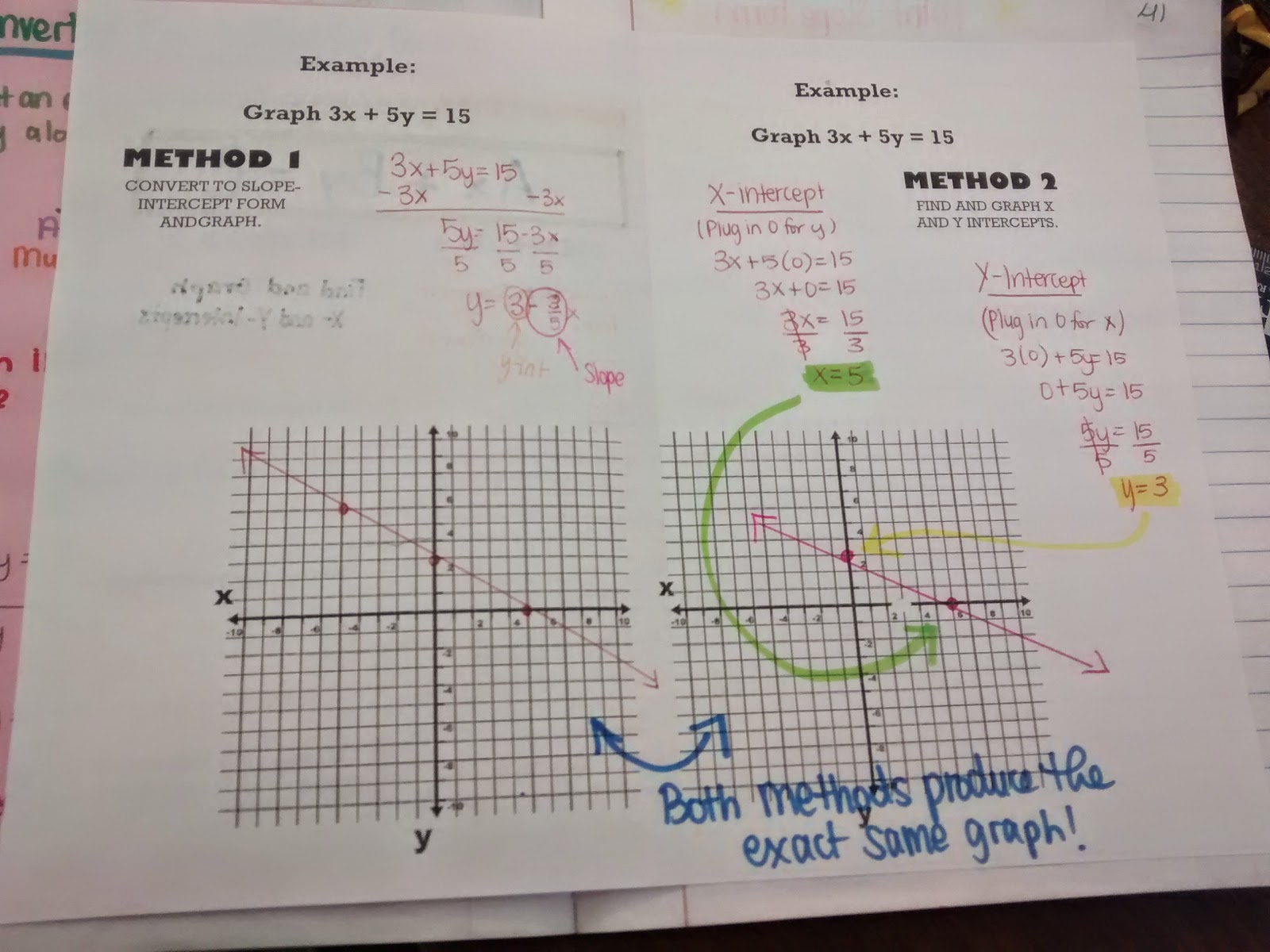
Here is a picture of our completed booklet foldable after being glued in our Algebra 1 interactive notebooks.

On the inside of the foldable, we solved the same problem using both methods.

Free Download of Standard Form of a Linear Equation Foldable
Print it double-sided and have students glue the blank side into their notebooks. I would suggest writing on it before gluing it in your notebook!
Standard Form of a Linear Equation Foldable (PDF) (2356 downloads )
I also created a standard form of a linear equation cut and paste activity for my students to complete that you might be interested in.

More Activities for Teaching Forms of Linear Equations
- Forms of Linear Equations Foldable
- Rearranging Equations for y Foldable
- Converting Equations to Slope Intercept Form Notes
- Point-Slope Form Dice Activity
- Different Forms of Linear Functions Foldable
- Linear Foldable y=a+bx
- Flyswatter Review Game for Different Forms of Linear Equations
- Point-Slope Form Foldable
- Standard Form of a Linear Equation Cut and Paste Activity
- Standard Form of a Linear Equation Foldable
- Slope Intercept Form y=mx+b Foldable









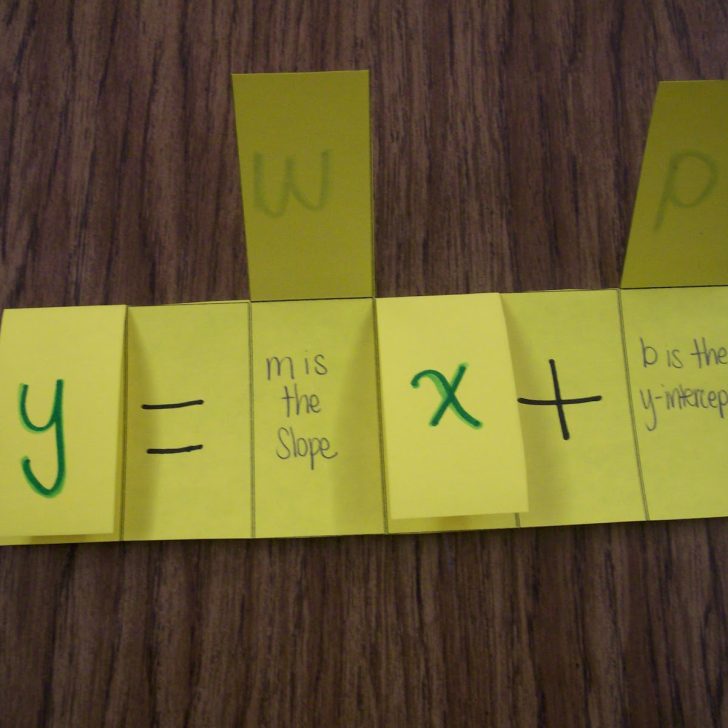



Loved that you shared these resources, your lesson, and reflections. We are working on that same unit. We did a thorough study of slope before beginning equations of lines. Then we worked through slope-intercept, point slope form, and standard form. We ended this week with transformations of lines. Students will be tested next week. But oh my – it does not bode well at this point! They struggle with solving for y; and they are struggling with graphing the lines. I'm looking for review activities – will consider your thoughts before finalizing my plans!
Do you have a link for the PDF? I'm super excited to use this!
I can't find the file in Box. What is it under? The links aren't showing up on this page.
I love this! Do you have a place where I can find the PDFs for your foldable and activity?
I searched all day Thursday and Friday on your blog for this specific link and could not find it anywhere! Today I'm preparing for the coming weeks and stumble upon it! Thank you so much, I love your blog and resources!
Glad you found it 🙂
Is the Standard Form foldable in the link? I didn't see it. . .
Found it on the second link. . . it wouldn't open the first few times. I use all of your ideas by the way. I absolutely love it and so do my students.
Sorry about that! The site that hosts my files is having some issues.
I cannot find your file for the cut out activity to convert from standard form to slope-intercept form. I've looked through you entire box folder.
Can you please share?
I'm really excited to use this on Monday with my students! We are solving systems of equations by graphing, and they are really struggling with remembering how to graph in standard form. I think this will be a great intervention for them. Thanks for sharing 🙂
Glad I could help!
Hi! Can you post another link, the one here do not work. Thanks so much!!!
That the Simplex Algorithm (pivoting) revises the scalars on the “Tableau of Detached Coefficients” in the way one computes them with matrix-vector algebra is verified by experience only! The revision formula for i neq i_{0}
bar{a_{i, j}} = ( a_{i, j}a_{i_{0}, j_{0}} – a_{i, j_{0}}a_{i_{0}, j} ) / a_{i_{0}, j_{0}}
with pivot a_{i_{0}, j_{0}} is not written in any textbook as if it is unnecessary. A “Fundamental Theorem of Simplex Algorithm” is due to be proven. Am I right?
Thank you so much for providing this resource! My son was absent from school today, and this is what his teacher used, so I was able to print it for him and now he will be less behind in class when he returns.