Coterminal Angles Card Sort Activity
I created this coterminal angles card sort activity for my trigonometry students to complete and glue in their interactive notebooks.

Students have to sort the angle cards into groups that are coterminal with one another. Then, they must take a blank square and write an additional angle that was coterminal with the other angles in the group.
This did not go as well as I had hoped. I’m not really sure why.

Free Download of Coterminal Angles Card Sort
New Reflections on Coterminal Angles Card Sort
During the 2016-2017 school year, I reused this card sort. Here are my reflections.
Due to a lack of time to create a new activity, I decided to use the same coterminal angle card sort that I created the last time I taught trig. This was not my original plan because this card sort went HORRIBLY last time I used it.

So, why did I decide to use the same activity that did not go well? Because I’m a different teacher now than I was two years ago. Two years ago, I had my students write notes for how to find coterminal angles. Then, I gave them the card sort and set them free.

That was not my approach. Instead, I gave my students the card sort. I didn’t have them cut apart the pieces YET. Instead, I had them get into groups and get one of our new giant, group sized white boards that I got courtesy of my schools’ foundation which awards grants to teachers.
I asked each group to take the 9 degree measures in the card sort and to sketch the angles on their dry erase boards.
Their work was messy and beautiful at the same time.

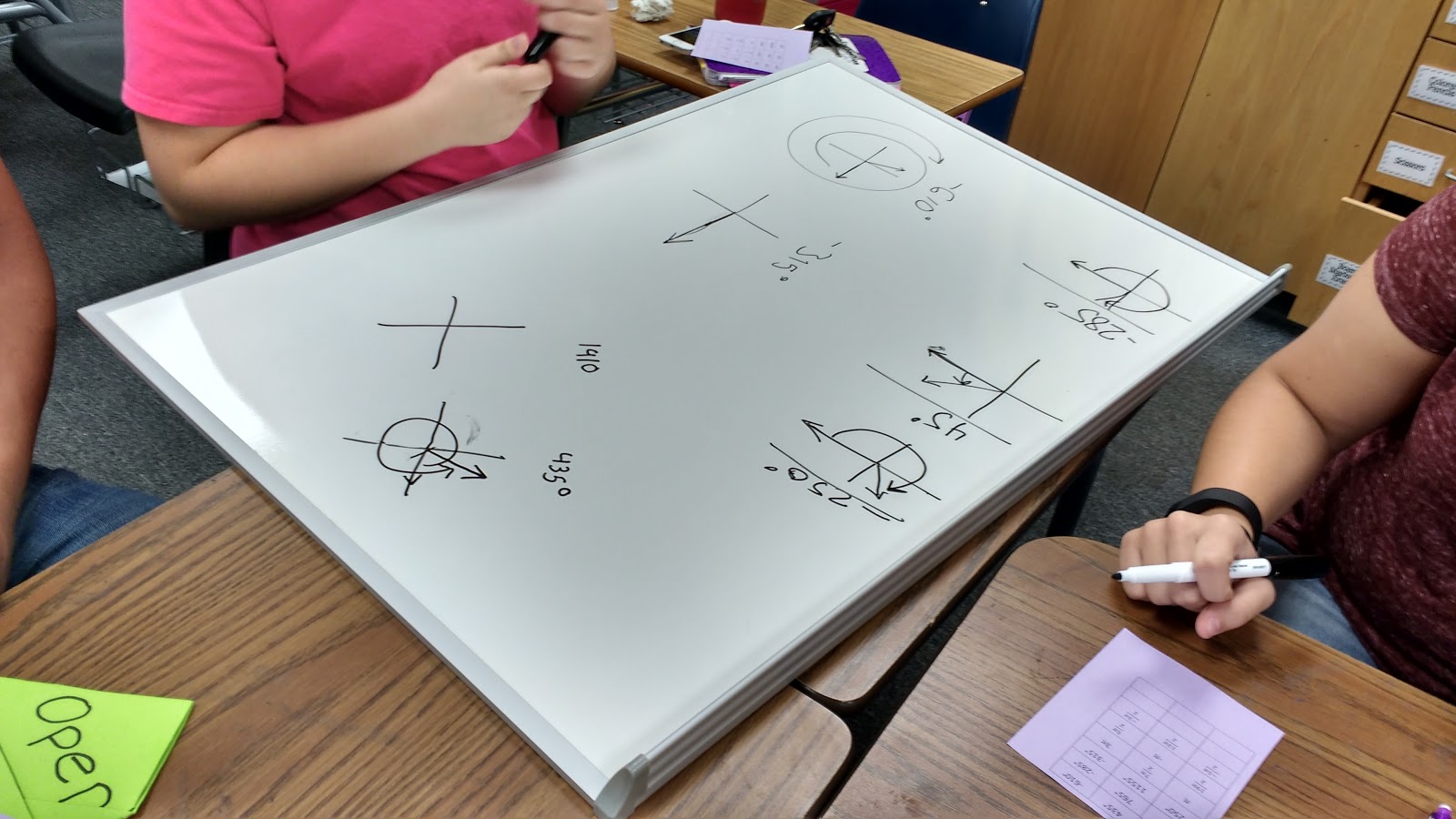
This student decided he wanted a whiteboard all to himself.

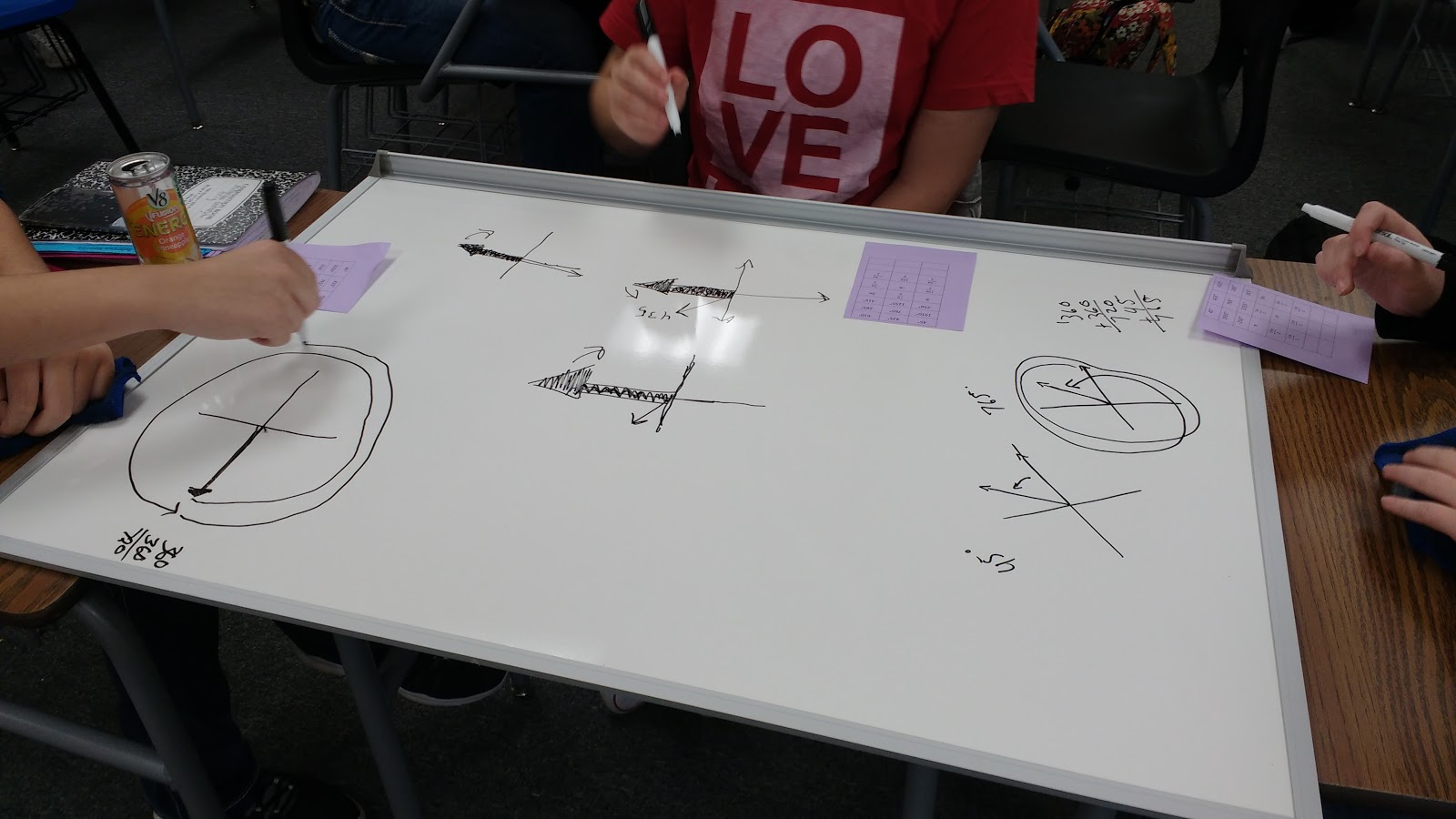
After sketching angles for a while, I asked students if they had noticed any similarities between the angles. They really hadn’t because different students were sketching their angles a bit differently. I gave them the definition for coterminal angles to help them out a bit. Then, I asked them to look at their sketches and determine which angles were coterminal.
I did give them a pretty big hint. There are 9 angle measures. They can be sorted into three groups of three coterminal angles.
With this new information, students kept working. Some groups began to get a bit frustrated when they couldn’t fit their 9 angles into 3 groups.

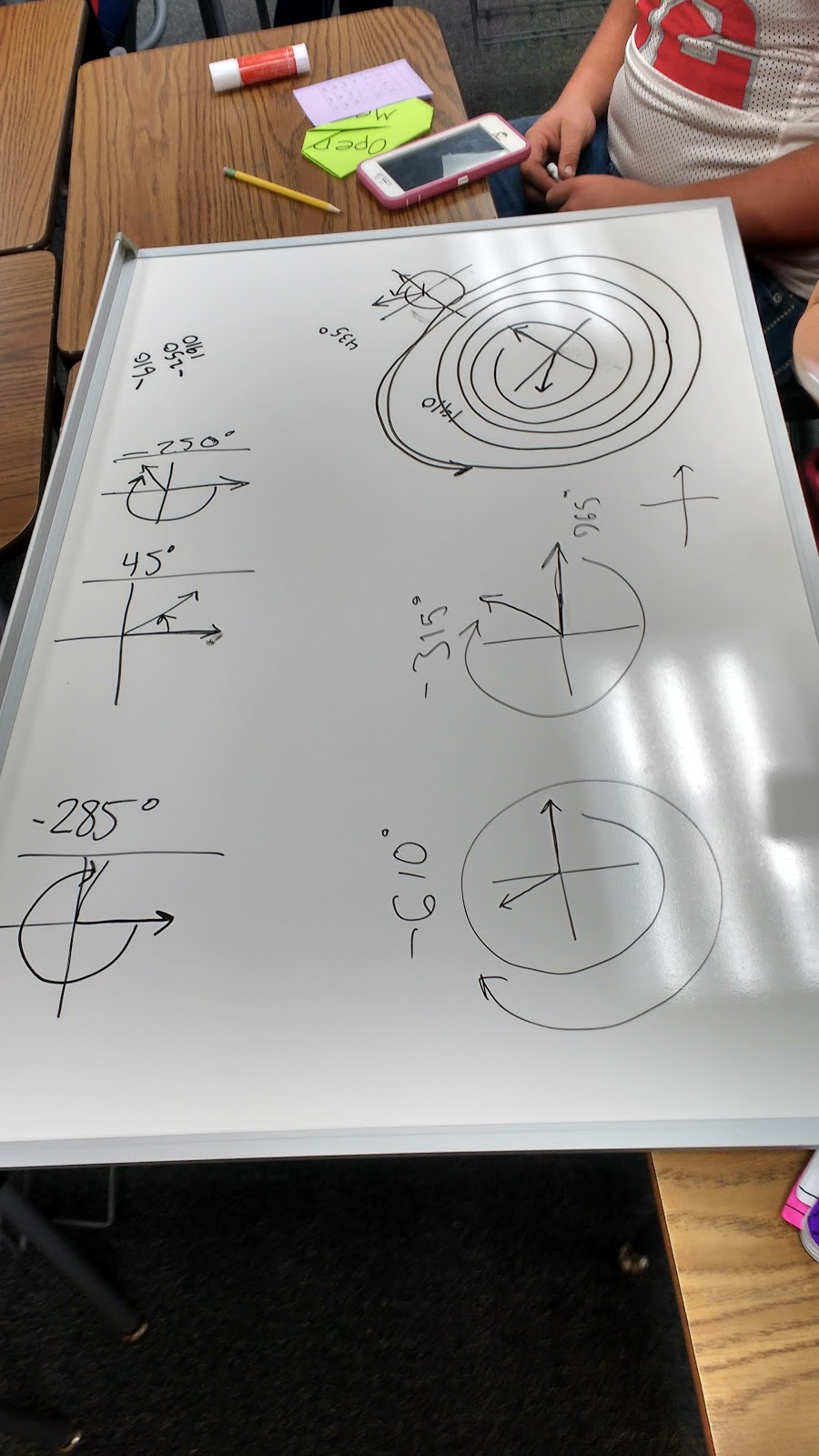
I took hold of this frustration and used it to encourage my students to think about what coterminal angles would have in common. I started by sketching a 20 degree angle on the dry erase board. Then, I asked students to come up with two coterminal angles of that 20 degree angle. They came up with -340 degrees and 380 degrees. Upon this discovery, I asked them how they could tell if two angles were coterminal based on this. One student piped up that coterminal angles were always 360 degrees apart. I challenged this. Are they always exactly 360 degrees apart? Then, a student corrected the statement. Coterminal angles are always multiples of 360 degrees apart.
And, that’s what is making the difference this year. I am not giving my trig students facts to memorize. I am giving them experiences that allow them to discover things for themselves. And, it is making ALL the difference!

When I directed my students to look at the radian measures and find the coterminal angles, they again wanted to convert all of the radians to degrees first. Again, I encouraged them to think about how we could deal with the radians without turning to degrees.
We already know that coterminal angles are multiples of 360 degrees apart. So, how many radians are they apart. 360 degrees is equivalent to 2pi, so coterminal angles are also multiples of 2pi apart. So, we did some review of adding and subtracting fractions, and we were well on our way. No degrees needed!

More Activities for Teaching Trigonometry
- Trigonometry Jokes and Puns
- Paper Plate Angle Spinners for Trigonometry
- Trig Reference Angles Activity: Odd One Out
- Evaluating Trig Functions Tarsia Puzzle
- 27 Hands-On Trigonometry Activities
- 5 Free Printable Trigonometry Posters
- Unit Circle Bingo Game
- Quadrants Unlocked Activity
- Printable Radian Sectors
- Trigonometry Calculator Skills Pop Quiz
- Odd One Out Coterminal Angles Activity
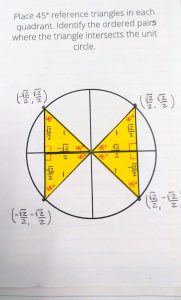
- Deriving the Unit Circle Foldable