Completing the Square Graphic Organizer

I created this completing the square graphic organizer for my Algebra 2 students to glue in their interactive notebooks after we explored completing the square with algebra tiles.

This student obviously did not pay attention when we were completing the square.  I guess he did complete the square, but…

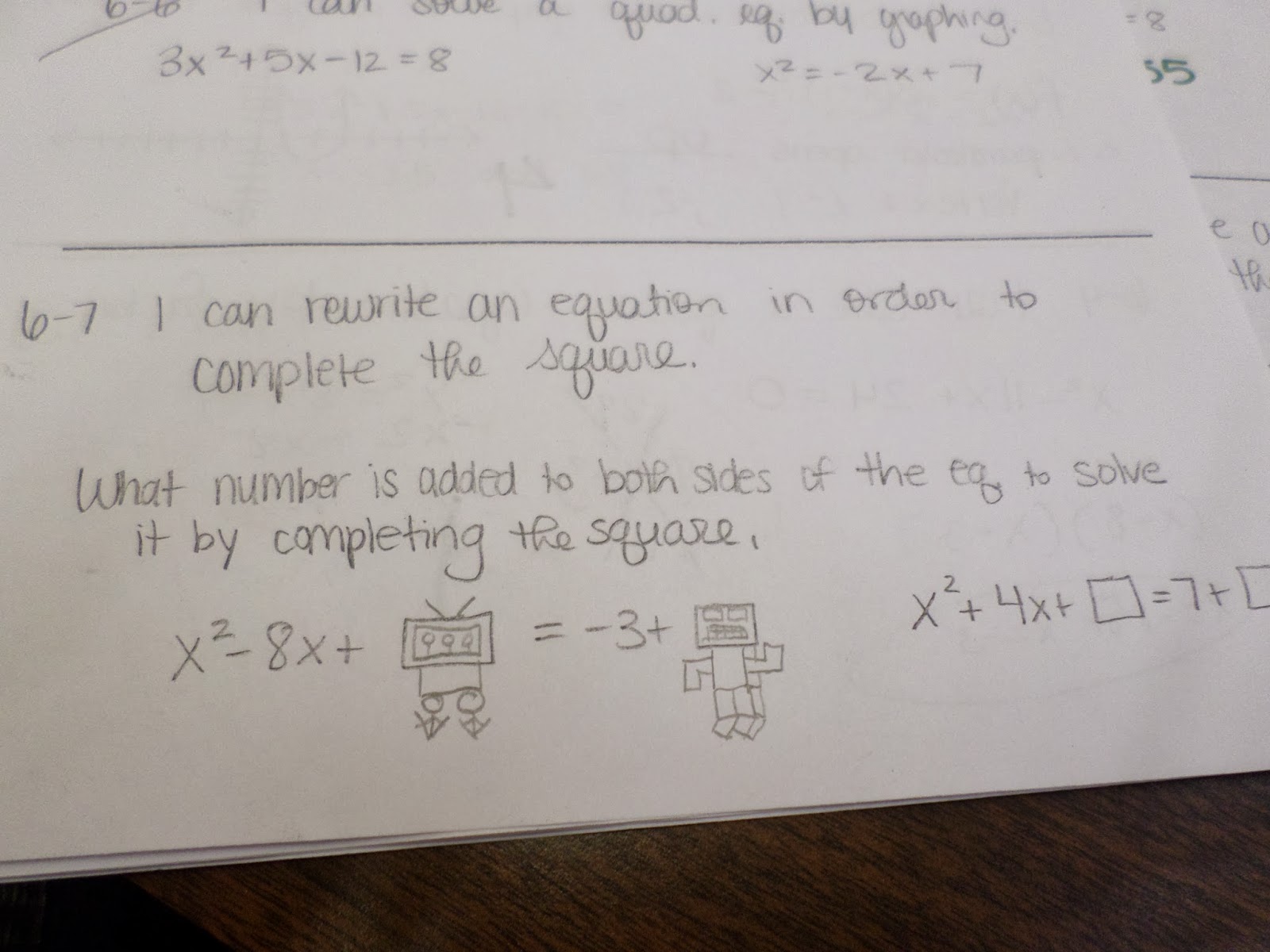
To illustrate completing the square, I got out a set of algebra tiles.  I only have one set of algebra tiles, so I used these under the document camera.  

I began by putting out the blue x squared tile and two green x tiles.  Class, how many yellow tiles are needed to complete the square?  One.

What if I have four or six green tiles?

We kept adding green tiles and determining how many more yellow tiles we would need to add.  Some students could visualize what we were doing.  

Others acted like this was the hardest concept in the world.

As we experimented, I had several students collect data in class.  If we have 2 green tiles, we need 1 yellow tile.  If we have 4 green tiles, we need 4 yellow tiles.  

As I started to run out of tiles, I asked the students to begin generalizing.  How many yellow tiles would I need if I had 26 green tiles?

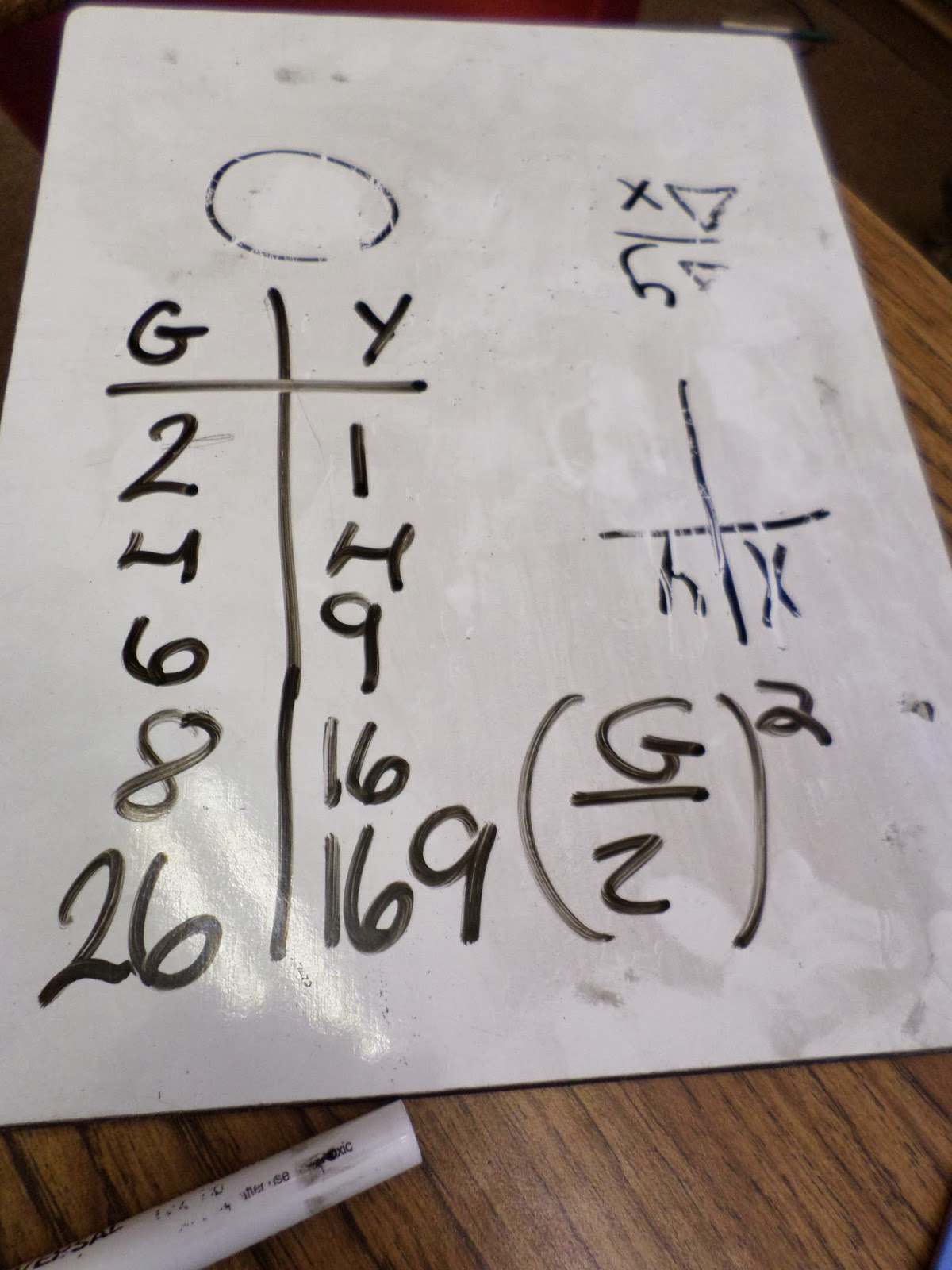
In each class period, one student ended up discovering that you halve the number of green tiles and square the result to find out the number of yellow tiles needed.  

After this discovery, we talked about how the number of green tiles represents the coefficient of the x term in our quadratic.

Only after discovering the formula for determining what to add to each side of the equation to complete the square did I pass out our notes to fill in.

I’m not completely happy with this lesson, but that’s normal.  Every year I strive to teach things better.  I learn by posting my stuff on the Internet for others to modify, tweak, and critique.

This student drew the algebra tiles on the side of their page to remind themselves of this process.  This was not required.  Awesome!