Modeling Function Machines with Flip Chutes Activity

Here’s a hands-on lesson I put together to teach my Algebra 1 students to evaluate and graph functions using function machines made of flip chutes.

Let me set the stage so you can see where this falls in my Algebra 1 curriculum.  At this point in the year, my Algebra 1 kiddos have reviewed the pre-algebra basics of the real number system, integer operations, and the order of operations.  We learned exponent rules and named polynomials.  We’re experts (hopefully) at distributing and undistributing (factoring) expressions.  Equations have been written and solved.  Inequalities have been solved and graphed (in one variable.)  Students have learned the definitions of relations and functions.  We’ve also discussed domain and range and independent and dependent variables.  We can graph points on the coordinate plane.  It’s now time to delve into function notation, expand on the idea of a function machine, and graph functions by making an input/output table.  We haven’t discussed slope or looked at the difference between linear and non-linear functions.  Those will come in the next unit.

When we discuss how to differentiate between a relation that is a function and a relation that is not a function, I introduced the concept of a function machine.  Humans like functional machines.  We like to be able to predict what’s going to happen.  When we put bread in our toasters, we expect toast.  If we put a toaster strudel in our toaster, we expected a warm, toasted toaster strudel.  If we put a bagel in our toaster, we expect a toasted bagel.  Because we know the function of a toaster (to toast things), we can predict the output based on the input.

What if this wasn’t the case?  What if I put in a piece of bread, expecting toast, and a toasted poptart comes out?  What if I sometimes get toast and sometimes get a poptart?  Life would certainly be exciting, but nobody in their right mind would buy that toaster for anything more than novelty purposes.  If I’m eating breakfast and I like poptarts, I might not be too broken-hearted if I put in bread and got out a poptart.  But, what if I’m wanting to make a BLT on toasted bread?  I definitely don’t want to eat my bacon, lettuce, and tomato sandwiched between two strawberry poptarts with lots of icing.  Yuck!  (And, for the record, my BLT would be made with MorningStar Farms Veggie Bacon.  I’ve never actually eaten real bacon.)

After introducing the concept of a toaster as a function machine, I ran across an amazing comment on Sarah Rubin’s Everybody is a Genius blog.  The comment was from Ms. Mac/Mrs. G.  And, she suggested showing students that a toaster allows several inputs with the same output.  But, it doesn’t allow one input to have several outputs.  For example, if I put wheat bread in my toaster, I get out toast.  If I put rye bread in my toaster, I get out toast.  If I put pumpernickel bread in my toaster, I still get out toast.  (I’ve never actually eaten rye bread or pumpernickel bread.  I guess I need to get out more!)  But, if I put in a bagel, there is no way that I could ever get anything but a bagel out of the toaster.  There is zero possibility of getting scrambled eggs or a waffle.  Every input has exactly one output.  I love this addition, and I think it will really help my students.  I’m definitely adding this to my unit next year!

I guess I made a pretty big deal out of my toaster analogy before Christmas.  After Christmas break, I asked the following question without really thinking about the whole toaster thing.

Me: “Guys, I brought some function machines from my house today.  Don’t you have function machines at your house?”
Student: “Did you bring your toaster?”
Me: “No… I guess a toaster is a function machine, but I brought a different type of function machine today.”

Now, remember the flip chutes I made this summer?  They are made out of saltine boxes.  Though, I’m pretty sure I was supposed to make them out of empty juice cartons.  They’ve been sitting in my house for months, just waiting to make their debut in this lesson.

I’m building up to the idea of function notation.  Last year, my Algebra 1 students had a terrible time wrapping their brains around function notation.  The whole idea behind this lesson is to try to avoid the frustration and confusion that seemed to persist last year with my students.  Why is the function notation necessary?  Because humans don’t just like predictable things.  They like things with names.  Here’s what I told my kids:

Me: “Humans love to name things.  We have an obsession with naming the things around us.  We name our children.  We name our pets.  We name our cards.”
Student: “We name our guns.” (That’s news to me.  Of course, I don’t actually own a gun.)
Another Student: “We name our shoes.”  (Yeah, I don’t do that either.)
A Third Student: “I give names to my favorite t-shirts.”  (That is yet another thing I don’t name.)
A Fourth Student: “I named my straightener.”

So, apparently, humans like to name things even more than I realized!  Mathematicians like to name things, too.  After all, they are humans.  Mathematicians are also fans of parsimony.  If they name something, they want to name it in the easiest and shortest way possible.  Therefore, usually the name of a function is notated by a single letter of the alphabet.  The word function starts with f, so a lot of times, mathematicians simply call a function f.

I have to function machines, so I named one f and the other g.  To further emphasize that f and g are just the name of the function, I gave them more traditional names, too.  Francine.  And George.  After I gave them these names, I realized that these are both the names of characters on Arthur.  I loved to watch Arthur when I was growing up.  I can remember being so scared of going to the third grade.  I mean, what if my teacher ended up being as mean as Mr. Ratburn?  Okay, enough with the reminiscing.

Once I realized that I was channeling Arthur with my names, I made a comment about it to my students.

Me: “I guess I’m channeling Arthur today.”
Student 1: “Who?”
Me: “You know!  Arthur, the aardvark.”
Student 1: “What?”
Me: “Have you really never seen that show on television?”
Student 2: “Oh, I know what show you’re talking about!  What did you say he was again?”
Me: “Arthur was an aardvark.”
Student 2: “He was an aardvark?!?  I always thought he was a bear!”

I didn’t realize that giving my functions names was going to lead to so many issues.  My 6th period class decided to rename George as Georgeio.  Another student came in at lunch to give me her opinion on the names.  “The function machines should be named George and Francisco.  Then, they can be gay, Italian lovers.  Italians make the best lovers.  I know this.”  I didn’t even respond to that comment.  I did not want any more details.

And, let’s not forget to mention the fact that Francine is taller than George.  One of my classes assumed that George and Francine were dating.  And, Francine is taller than George.  The girl is taller than the guy.  Oh, what outrage!

Next, it was time to take some notes over function notation.  I have shared this Function Machines and Function Notation Foldable on my blog as well.

These notes were heavily influenced by (read: stolen from) Everybody is a Genius.  We labeled each part of a function in function notation.  And, then we practiced evaluating functions using a function machine.

I’m going to be really honest.  After going over the parts of a function, my Algebra 1 kids were VERY confused.  But, after we worked through the two examples with the function machines at the bottom, light bulbs started going off.  “Oh, that’s what that means!”

Inside the foldable, students were given two new functions to evaluate for various inputs.

I included some problems where students added functions and found the composition of functions.  Normally, I would have skipped over these because they are not tested in Algebra 1, but I’m slowly starting to work in increasing the rigor of my Algebra 1 class in preparation for Common Core.  I also included two problems at the bottom where students had to evaluate the function for a different variable.

On the right side of the inside of the page, I include 3 sample EOI questions for students to solve.  I want my students to be familiar with how the questions will be phrased on their end-of-instruction exams.

This took probably 2/3 of our 50-minute class period.  For the last third of class, we started a hands-on activity using my shower curtain coordinate plane and the function machines.

Before class, I prepared five pairs of functions.  Each pair of functions f and g were written on a post-it note.  Since I have a limited domain and range on my shower curtain, I prepared cards for each ordered pair of the function that fit my restricted domain and range.

Here’s a close-up of the cards in one bag.  The post-it note is a reminder for me.  It tells me what functions to write on the SMART Board.  One one side of the cards, students are told what to solve for.  For example, if a student picks up a g(2) card, they know that they are finding the output that results from putting 2 into g.  The resulting output is written on the other side of the card.

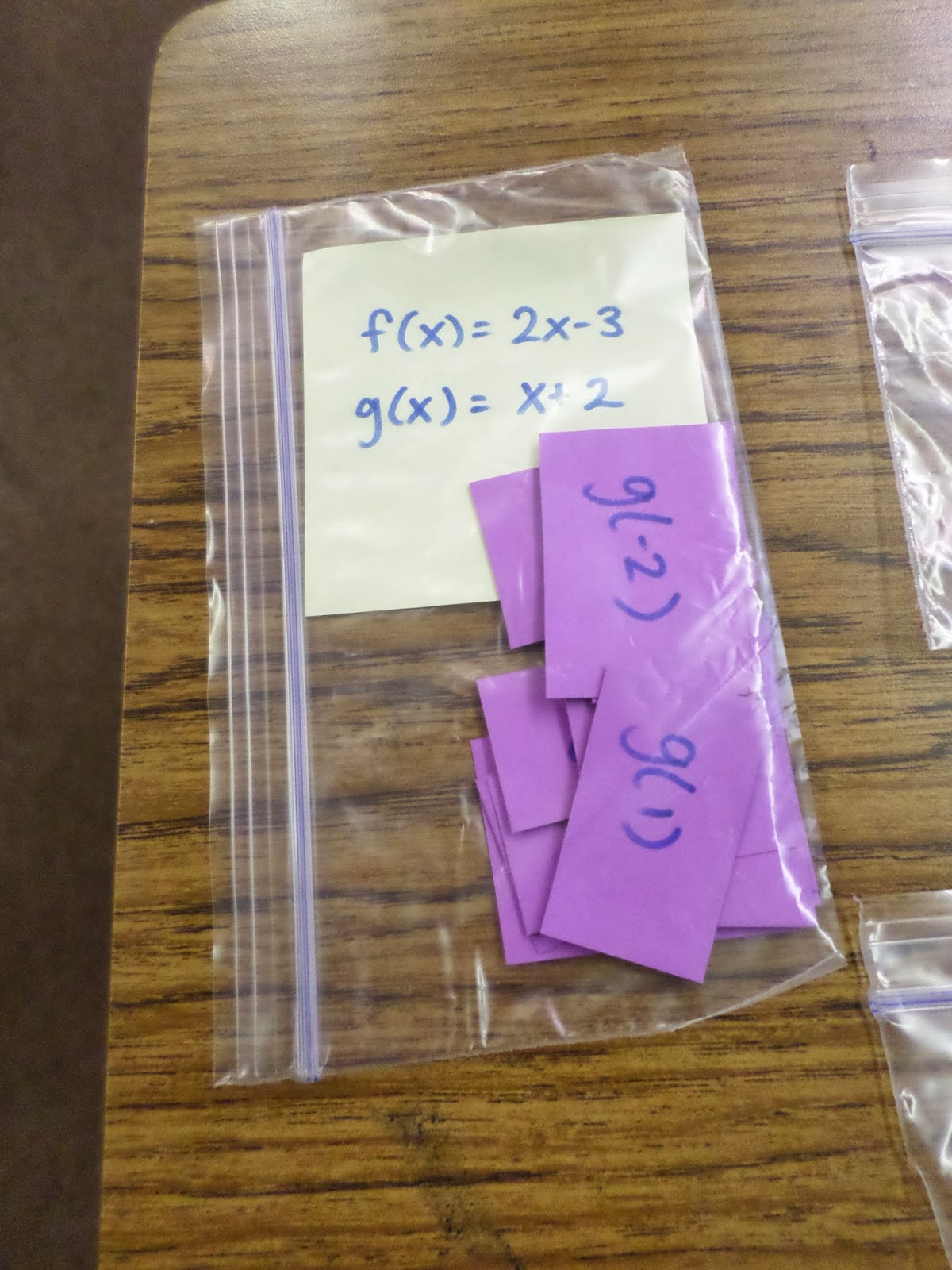
To give students an element of choice, I laid out all of the cards on the desk.  Students were instructed to pick a card up off the desk and return to their seat.  At their seats, they have calculators, dry erase boards, markers, and erasers.  The students were to evaluate the correct function for the given value of x.

If a student picked up the f(3) card, they would return to their seats and substitute 3 in for x in the function f(x) = 2x-3.  They should get an output value of 2(3)-3 = 6-3 = 3 if all their work was done correctly.  Once they have an answer, they must go back to the function machine and feed the problem to the function machine.  This is their input.  They feed the input into Francine because they were asked to plug the 3 into f.

This is where things get cool.  Upon placing the f(3) card in the function machine, the function machine will flip the card over so that it comes out reading 3.  To the students, it is MAGIC!

I would LOVE to set up a video camera to capture my students’ faces the first time they put a card in the function machine.  Their expressions are priceless!  Of course, they soon realize that the answer is written on the back of the card.  And, all the function machine does is flip the card over.  Even after discovering how it works, they still seem to love it.  I might have seen one or two kids all day forgo feeding their cards into the function machine and just flip it over to check their answer instead.

I like that this got my students checking their answer, and I hope that it reinforced the idea of inputs and outputs. After checking their answer, students now had to graph their input and output as an ordered pair on the coordinate plane.  My giant coordinate plane was put in the floor for this activity.

To plot the points, I created points out of some giant foam stars that my sister had given me.  She had used part of them for an art project.

To further emphasize function notation, I labeled the stars with generic ordered pairs.  (1, f(1))  or (5, g(5)).

I was hoping that students would make a connection between the fact that f(0) means the output of f when the input is 0.  I guess I didn’t do the best job of explaining this on Day 1 because my students did really well until we got to the graphing part.

Instead of nice linear functions, our attempts usually ended up looking a little something like this.

After graphing each point, students picked up a new card and repeated the process. They placed the cards that had been graphed on top of the function machines to avoid further confusion.  Once all the ordered pairs had been found and graphed, we had a class discussion.

What stars look like they are in the wrong place to you?  A student would pick a star that they believed was incorrect.  And, as a class, we would evaluate the function for that value and determine the correct place for it to go.  Sometimes the star had been placed correctly.  Most of the time, however, students made the exact same mistake.  (3, f(3)) would be placed on (3, 3).  (-2, g(-2)) would be placed at (-2, -2).  Students were seeing the input of the function and were confusing that with the output.

Here’s an example of some mis-placed stars.

Eventually, after some hard work, we concluded that all the stars were now in their right places.

Students were shocked to discover that the points formed two lines!  Will this always happen?  Students were convinced that sometimes they would make lines.  Other times they would make X’s.  After graphing one pair of functions, time was up.

I felt like we had made some progress, but I knew we had so much more to go.

Enter Day 2.  We started off class by watching the Meat-A-Morphosis: An Introduction to Functions video from YouTube.

If you haven’t seen this video before, take seven and a half minutes and just do it!  I told my students that we were going to watch a movie, and they were instantly excited. I show lots of math songs and short youtube clips, but I tell my students that I don’t believe in movies.  They think that we should be watching feature films before every single holiday.  Ummm….no.  I have way too many exciting mathematical things to share with them.  I don’t have time for us to watch Finding Nemo.

They soon realize that we are watching another math video, so their excitement fades.  When the music starts, the complaints start up again.  “How old is this movie you’re making us watch?!?”  “I don’t know.  Just watch and see.”  The girls ooh and aah over how cute the little chickens are.  The class collectively gasps when the (spoiler alert) chickens are chopped up to make chicken nuggets.  “Why are you showing us this?”  “Wait!  You’re a vegetarian.  Why are you showing us a video about meat?”  “Guys!  I think she’s trying to turn us into vegetarians!”  No, I’m trying to turn you into mathematicians.  At the end of the video, one particularly opinionated student said, “Some of the things I see in here scare me.”

At this point, I’m still frustrated over my students’ struggle with function notation from the previous day.  How do I fix this?  I know!  We’ll do an example problem, and I’ll force them to use function notation an obnoxious number of times!

Graphing Functions on the Coordinate Plane Graphic Organizer.

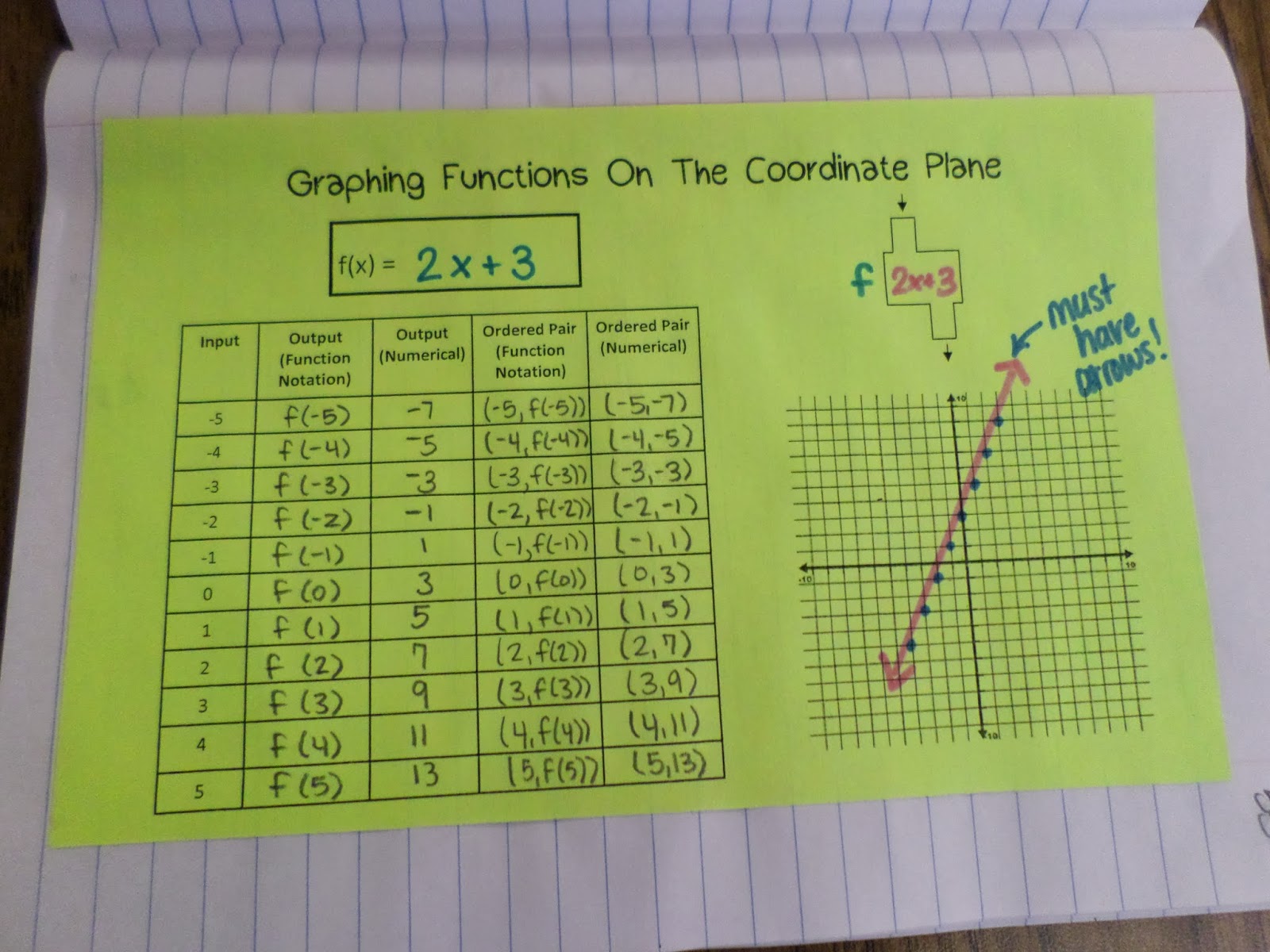
I gave the class a function to graph in function notation.  And, I also gave them their inputs, the integers from -5 to 5.  Students had to write the output in function notation, the output as a number, the ordered pair in function notation, and the ordered pair using only numbers.  We did the first two lines of the table.  Then, I gave students several minutes to work.  We would check their work, and they would continue on.  It was time-consuming, but I think it was a positive learning experience.

It was awesome to see students start to make connections.  Some realized they could very easily fill in the function notation columns.  Others noticed that the numerical output increased by two every time.  I walked around the room, pointing at student work, congratulating them on finding patterns.  We graphed the ordered pairs, and they formed a line!

With about fifteen to twenty minutes in class, we once again tried graphing functions using the function machines, cards, stars, and shower curtain coordinate plane.  When students looked confused, I reminded them of the function notation we had just used earlier that day in our notebook.  That seemed to help some.  But, I still had some very frustrated kiddos who could not figure out how to pick out which star to use or where to place it on the coordinate plane.

I was starting to write off this whole exercise as a failure.  Maybe I am just terrible at teaching function notation.  Maybe my kids are just doomed to never understand this.  I wasn’t about to give up, though.  My students were going to understand function notation one way or another!

The next day, I decided we were going to spend our entire 50-minute period graphing functions.  If we continually graphed, checked our work, discussed discrepancies, and tried again, they were bound to have to get it!  I had students open their notebooks to our pages on function machines and function notation to use as a reference.

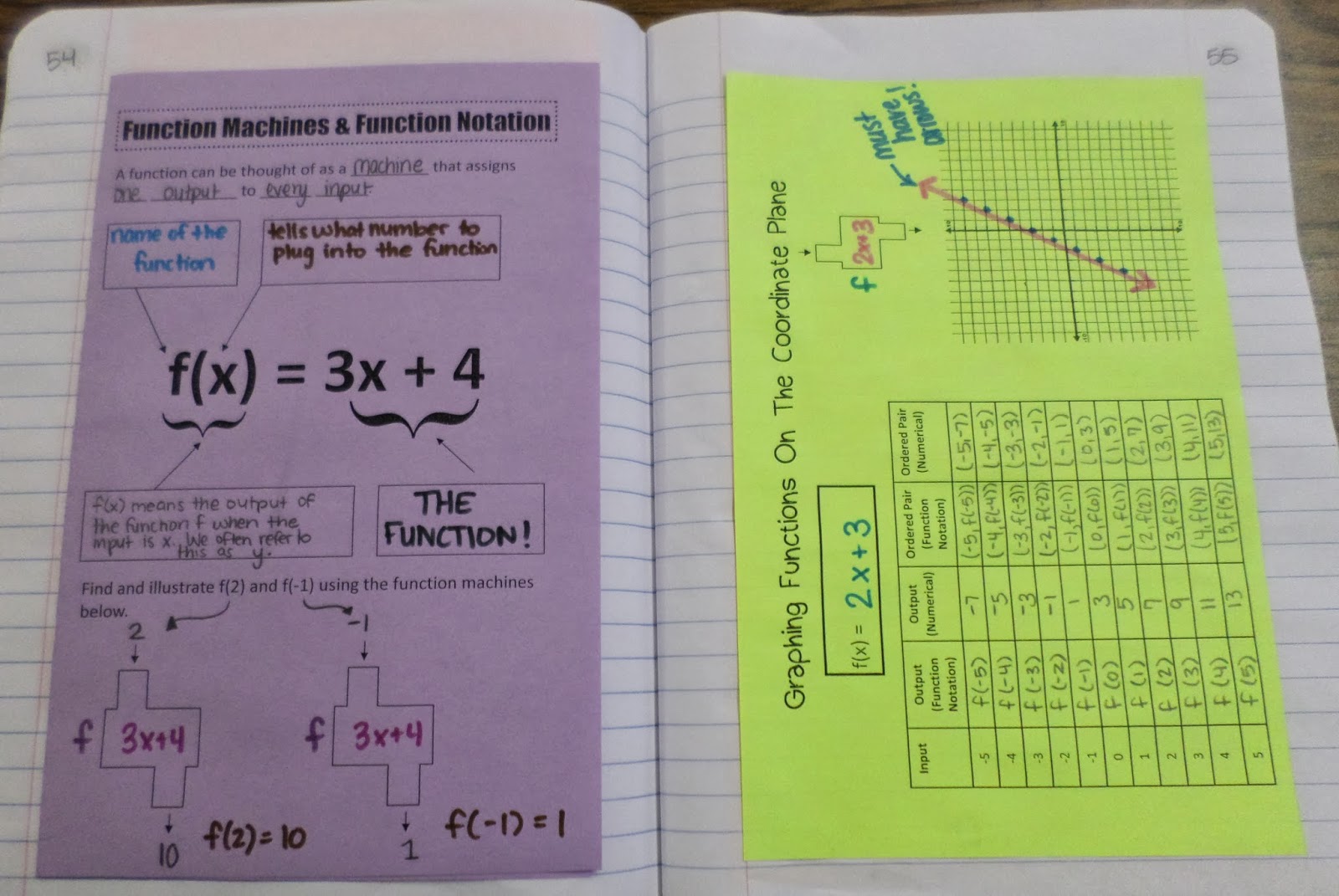
My students were rocking the process of evaluating the functions.  They were checking their answers using the function machines.  Life was good.  Well, life was good until they got to the stars.  I decided to just position myself by the stars and help students with the graphing process.  They were going to get this!

After helping student after student find their correct star, I had an epiphany.  They already have the card in their hand that has the output written in function notation on one side and the output written in numerical notation on the other side.  Why don’t I have them use this card to graph their ordered pairs?!

My conversation with students went something like this.

Student: “I can’t figure out which star I need!”
Me: “Well, what was your input?”
Student: “My input was 2, and my output was 1.  But, I don’t see a star labeled (2,1).”
Me: “Do you remember how we had two different ways of writing the output in our notes?”
Student: “Yes.”
Me: “Well, if your card says f(2), you need to find a star that also has f(2) in the ordered pair.”

Problem solved.  Find the star that matches the card.

This was great except for the fact that they still wanted to put the (2, f(2)) star on (2, 2).  Every.  Single.  Time.

It was time for a second epiphany.

Me: “So, your output was f(2)?”
Student: “Yes.”
Me: “And, what was the numerical output that you got when you plugged 2 into the function?”
Student: “When I plugged in 2, I got 1.”
Me: “So, f(2) is 1?”
Student: “Yes, I just said that.”
Me: “So, you’re saying that f(2) is equal to 1?”
Student: “Yes. f(2) equals 1.”
Me: “If f(2) equals 1, then I can replace the f(2) with 1.  And, that will tell me where to graph the ordered pair.”

At this point, I made a show of flipping the card over several times.  I would show them that (2, f(2)) was the exact same as (2, 1).  After all, they had just told me that both sides of the card meant the same thing.

All of a sudden, my students were graphing points like nobody’s business.  They didn’t need my help to find their stars.  And, they certainly didn’t need my help to graph their ordered pairs.  It was so fun to watch them match the cards with the stars and then lay the cards on top of the stars.  They would flip the card over just like I had shown them in order to graph their ordered pair.  Success!

My students were able to successfully graph horizontal lines and quadratic functions using the function machines as well.  We ended up calling f(x) = 3 the Spam equation.  No matter what our input, 3 (spam) always comes out.  (If you’re confused by this, you should really go back and watch the Meat-A-Morphosis video.  I promise; you’ll be much less confused!)

So, why do I love this lesson so much?

It’s hands-on.  It got my kids out of their seats.  It was self-checking.  It was a safe environment to make mistakes.  When students point out that they think (3, f(3)) is in the wrong place, nobody knows who graphed that point unless the student announces that it was their star.  Each student worked at their own pace.  It was discussion-provoking.  Students were craving vocabulary words like slope and y-intercept that we had yet to learn.  They were asking questions, making predictions.  “I bet this one makes a line, too!”  After, we graphed a quadratic, one student wanted to know how he could tell from the equation if the graph would make a straight line or a parabola.  I also felt like I could differentiate this activity for my students.  If f(x) was a quadratic and g(x) was linear, I could push my advanced students toward solving the f(x) cards, and my students who needed more support could be further practicing linear functions with the g(x) cards.

Basically, I want this to be what my classroom is like every single day.