Prime Factorization Graphic Organizer
I created this prime factorization graphic organizer for my Algebra 1 students to summarize two different methods for finding prime factorization: the factor tree method and the birthday cake method.

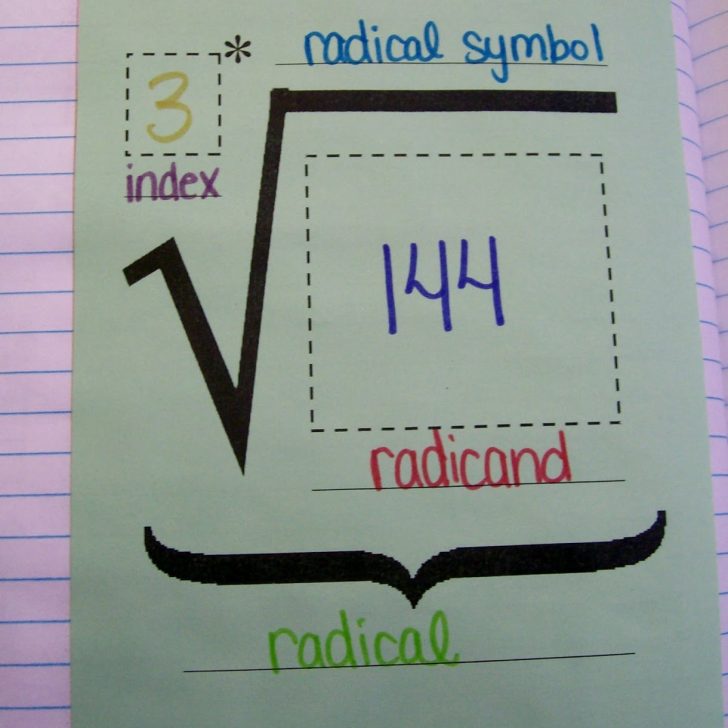
I teach my Algebra 1 students to simplify radicals through prime factorization because it works no matter what the index of the radical is. This means we need to do a quick review of prime factorization since it’s been awhile since they’ve seen this.

Most of my students learned prime factorization with the factor tree method. This is how I learned it as well.

When I was student teaching, I was introduced to the birthday cake method. I find that my students make WAY less mistakes when they use this method. There’s just something about the fact that the prime factors are arranged linearly that helps them make sure they didn’t miss a factor.
Of course, I let my students choose which method they prefer. In each class, there are students who are devoted fans of each method. When I do problems myself, I actually find myself switching between methods depending on which seems easier for that problem.
Many students prefer the factor tree method because you can start with ANY two numbers that multiply to the given number. Then, you proceed with finding factors until all of the factors are prime.

The reason I try to steer students away from the factor tree method is that it can get messy. I have seen too many students do a factor tree like the problem above and write the prime factorization as 2^2 * 3 * 5 instead of 2^3 * 3 * 5.
The birthday cake method can take a bit longer to get started because you must find a prime number that divides into the given number. You can start with any prime number that divides into the number, but many of my students choose to use 2, 3, 5, 7, etc in that order.

I love that the birthday cake method is so streamlined. Instead of searching for all of my prime factors in a tree, my prime factors are all lined up nicely for me.
Free Download of Prime Factorization Graphic Organizer
Prime Factorization Graphic Organizer (PDF) (1375 downloads )
Prime Factorization Graphic Organizer (Editable Publisher File ZIP) (895 downloads )
More Activities for Teaching Prime Factorization
- Free Printable Factors Chart 1-100
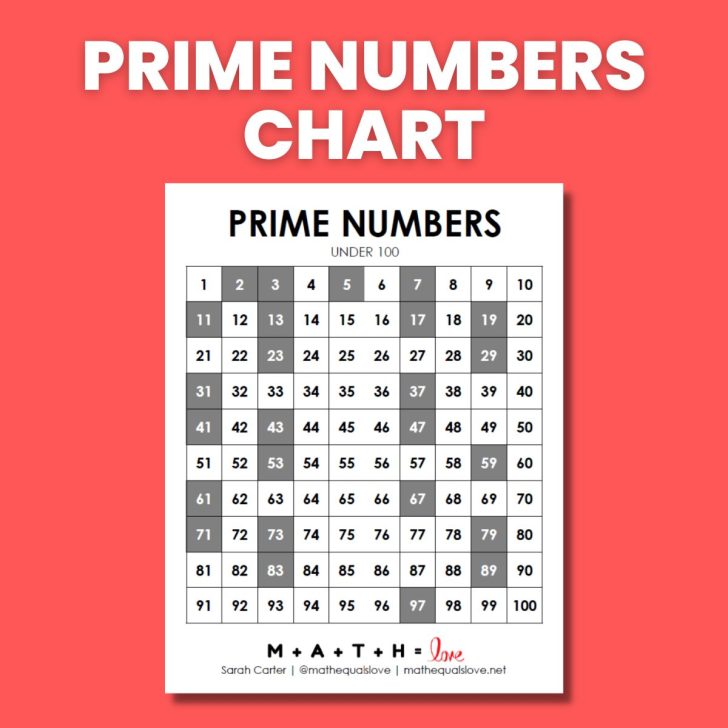
- Prime Numbers Chart
- Factors Race Activity
- Prime Factorization Foldable
- Prime Factorization Graphic Organizer
- Factor Tree Puzzles Inspired by Dr. Harold Reiter
- Prime Numbers Below 100 Chart
- Prime Factorization Practice Booklet
- Prime Numbers Poster
- Prime and Composite Numbers Chart
- Prime Factorization using the Birthday Cake Method
More Activities for Teaching Radicals
- Prime Numbers Chart
- Radicals Task: Which is the Smallest?
- Like Radicals Card Sort Activity
- Parts of a Radical Poster
- Prime Factorization Foldable
- Prime Factorization Graphic Organizer
- Prime Numbers Below 100 Chart
- Simplifying Radicals Puzzle
- Rationalizing the Denominator Practice Book
- Operations with Radicals Question Stack Activity
- Conjugates INB Page
- The Constant Chair Regression Activity
- Prime and Composite Numbers Chart
- Multiplying Radicals Graphic Organizer
- Vocabulary Knowledge Rating Chart
- Parts of a Radical Graphic Organizer
- Radical Clock Makeover
- Dice Activity for Reviewing Square Roots