Reviewing One Variable Inequalities

On Friday, my Algebra 1 students started to review inequalities.  It was so refreshing to see them realize that this was something they had studied last year in 8th grade.  A few students mentioned that they had never figured out how to do these problems last year, and they asked lots of awesome questions.

Including the “not equal to” symbol provided all of my students with a challenge since that’s something they most definitely did not see in 8th grade math.  Seeing light bulbs go off as they realized that we would need to shade BOTH ways was priceless!

We did a quick foldable that I created and blogged about back in 2013.  This is one of the few foldables that I seem to use year after year after year without editing it.

I have a different student volunteer to make an example statement for each symbol for us to graph on our number lines.  Most kiddos like to pick a variable that corresponds with the first letter of their name.

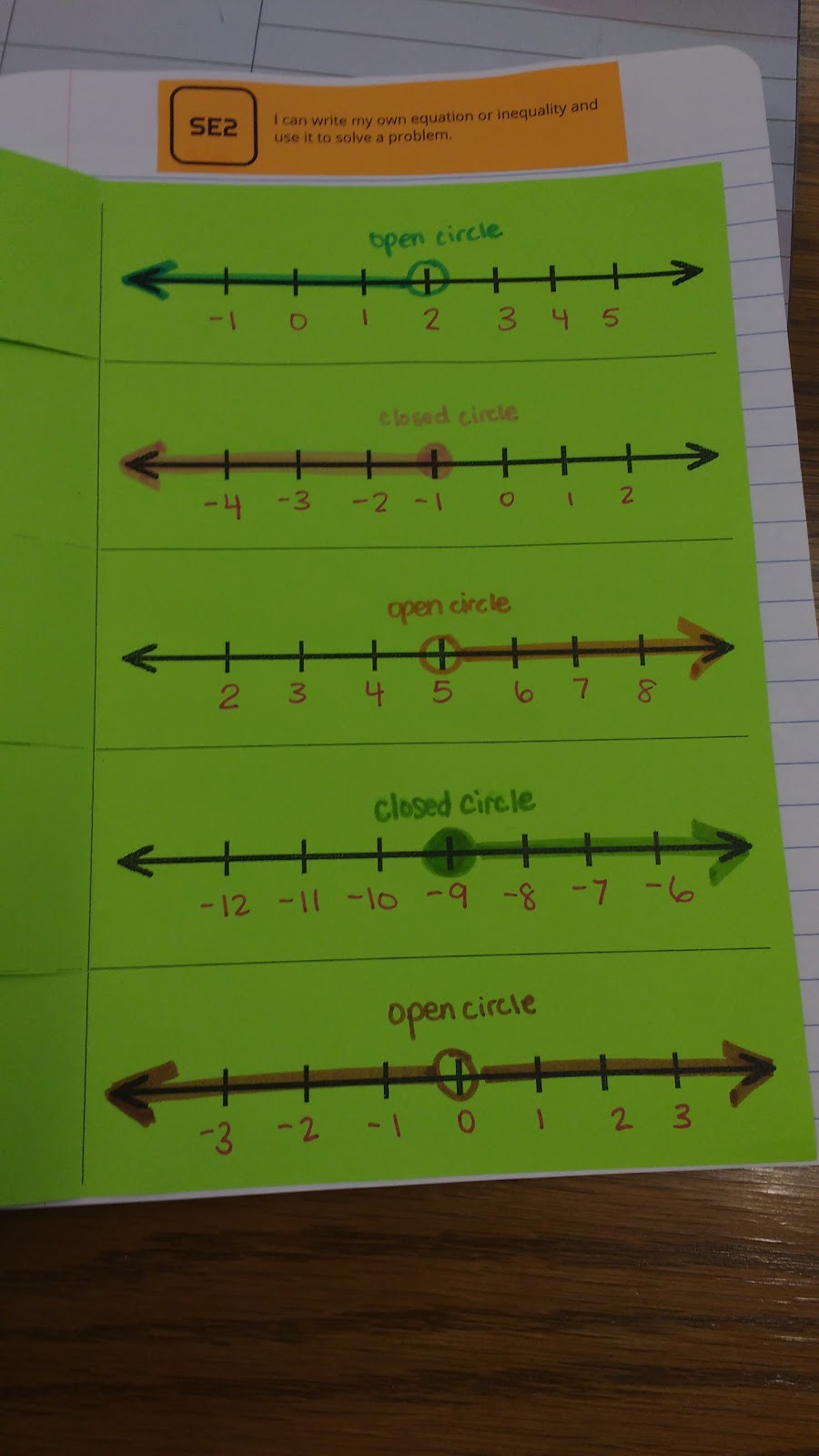
After reviewing the various inequality symbols and discussing how to graph them, we did the “Toe the Line” investigation from Discovering Algebra.

I used the snipping tool on my computer to cut out the table and paste it in a Publisher file to make an interactive notebook page.

With my first period, I had two students stand in front of the appropriate places of my number line and walk through the activity.  It went TERRIBLY.  (On a happy note, you can find out more about my classroom decorations here.)

With my next two classes, I had them use their imagination to pretend there are two people walking along the number line.  This worked SO much better!  In both classes, one student told the class that the symbol was always going to be “less than.”  With each line on the table, they became more and more adamant that it was always “less than.”  After writing 7 less than symbols in a row, they were even more convinced.  Then, we multiplied both sides of the inequality by a negative number, and there were audible gasps in the room.I made my students take their marker or highlighter and circle each of the steps that made the inequality symbol change.  Some of my students claimed that multiplying and dividing is what changed the symbol.  Other students recognized the need for multiplying or dividing by a NEGATIVE number.

The one problem I have with this activity is that it never asked my students to divide by a positive number.  This activity is a definite keeper, but I want to make my own table for next year.  I’m disappointed that it worked better as a sit and write activity than a get up and move around activity.

The last thing I did with my students to review inequalities was to run a quick session of “Graphs of Inequalities Speed Dating.”  It was so hard to put these black boxes on my precious students’ faces because they were all smiling.  They were doing math AND enjoying it!

I wish I had files for this activity to share, but I don’t because they are just handwritten on index cards.  The front of each card has the graph of an inequality.  The back of the card has the inequality written in words.  For example, the back of the card might say “x is greater than or equal to 7.”  This lets students

Tomorrow, we’ll be starting to write our own inequalities based on story problems.  It’ll be interesting to see how that goes!

More Activities for Teaching One Variable Inequalities

• 
  Solving Equations/Inequalities with Variables on Both Sides Graphic Organizers
• 
  Compound Inequalities Graphic Organizers
• 
  Solving Equations/Inequalities with Variables On One Side Graphic Organizers
• 
  Inequalities Investigation
• 
  Graphing Solutions on a Number Line Speed Dating Activity
• 
  One Variable Inequalities Card Sort Activity
• 
  Compound Inequalities Foldable
• 
  Reviewing One Variable Inequalities
• 
  One Variable Inequalities Square Puzzle Activity
• 
  Graphing Inequalities Foldable
• 
  Inequalities Foldables