Real Number System Graphic Organizer
This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.
While looking for inspiration, I found a lot of creative illustrations of the real number system. But, I was looking for something a little different. I wanted my students to add the information.
And, for my older students, I wanted them to even discover some of the information themselves before we added it to the graphic organizer as a class.
So, I created my own real number system graphic organizer that would meet all my needs.

For my Algebra 2 students, I plan to give my students strips of numbers. Each strip will correspond to one of the subsets of the real numbers. It will not be labeled however. I want them to take these numbers and try to figure out how they nest on to the graphic organizer.
I’m hoping that they will discover for themselves that every natural number is a whole number, every whole number is an integer, etc.
I ran across this in a pile of math resources I was given. Something to think about:

I am using interactive notebooks with my Algebra 1 and Algebra 2 students. So, I plan to have students glue the real number system graphic organizer in their INBs.
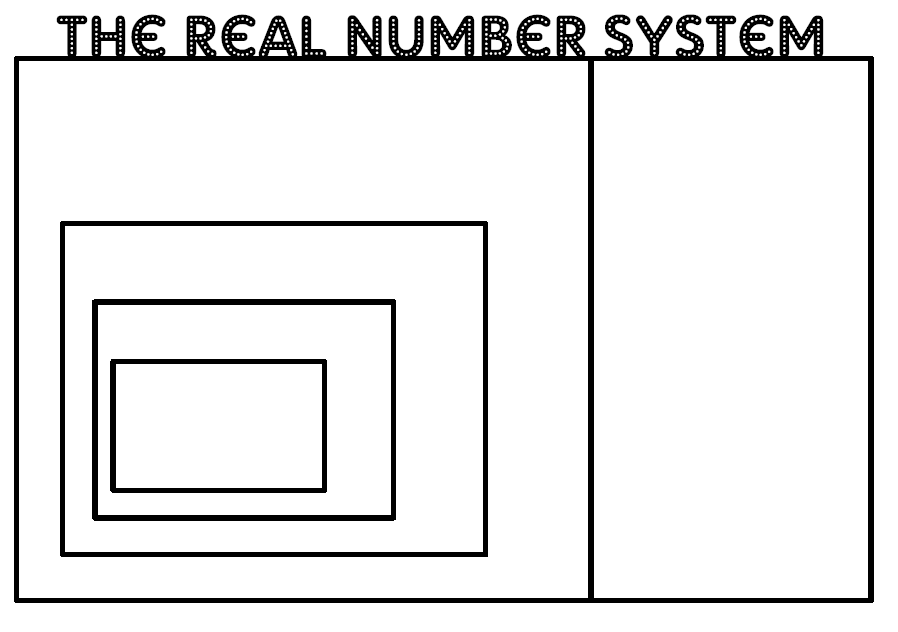
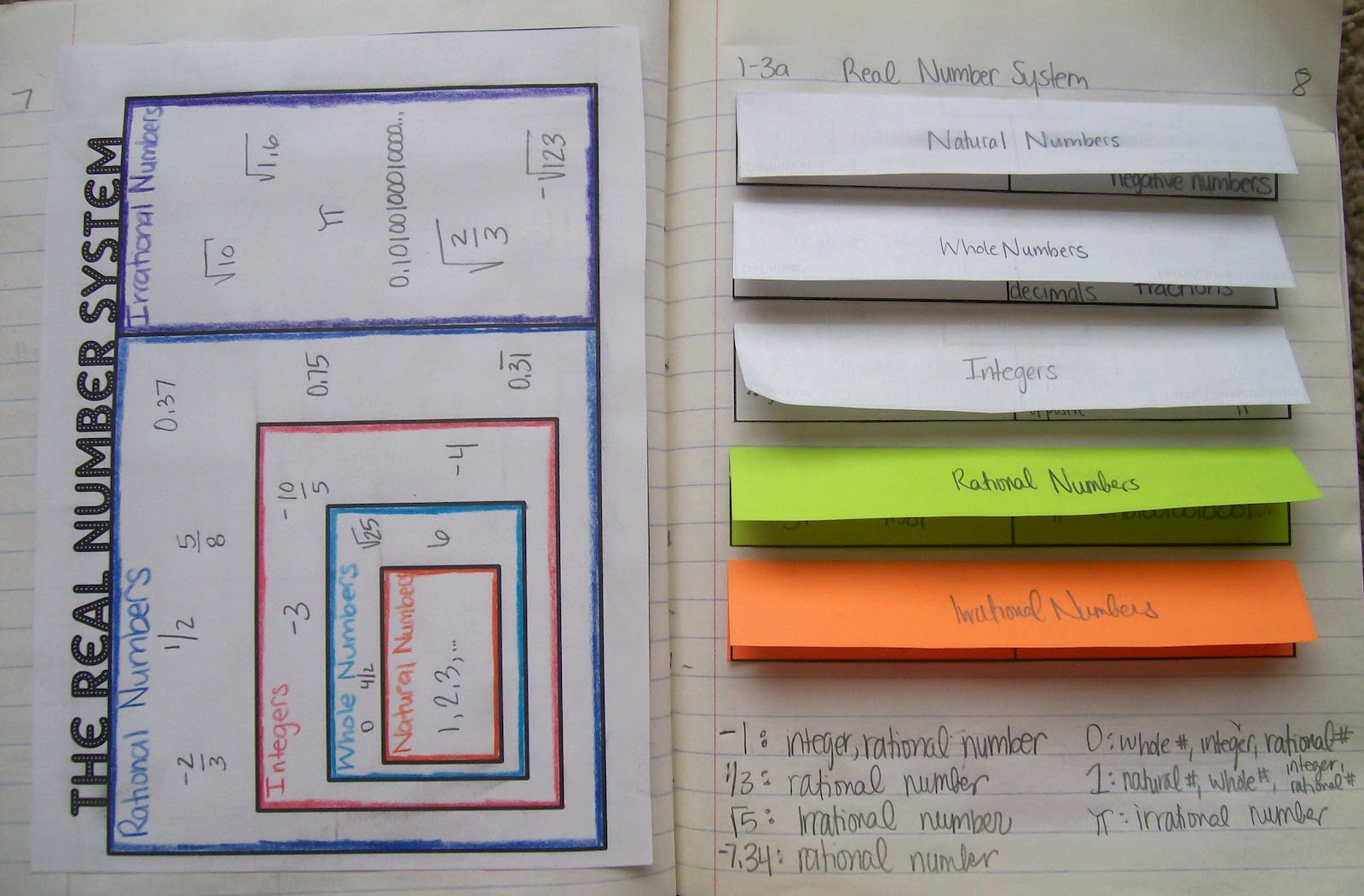

I want the students to outline the boxes with colored pencils to emphasize the fact that everything inside the red box is an integer, even the whole numbers and natural numbers.

So far, I just have definitions (Frayer Model) and a few examples. Obviously, my final draft and sample notebook will be neater. And, the rational numbers and irrational numbers are only a different color because I already had some printed on colored paper.
In real life, they would either be all white or all different colors. Trying to overcome my perfectionism here…
In 2013, I used the same graphic organizer for the real number system, but we filled it out slightly differently. It felt good to be able to reuse something from last year instead of creating something entirely new from scratch!
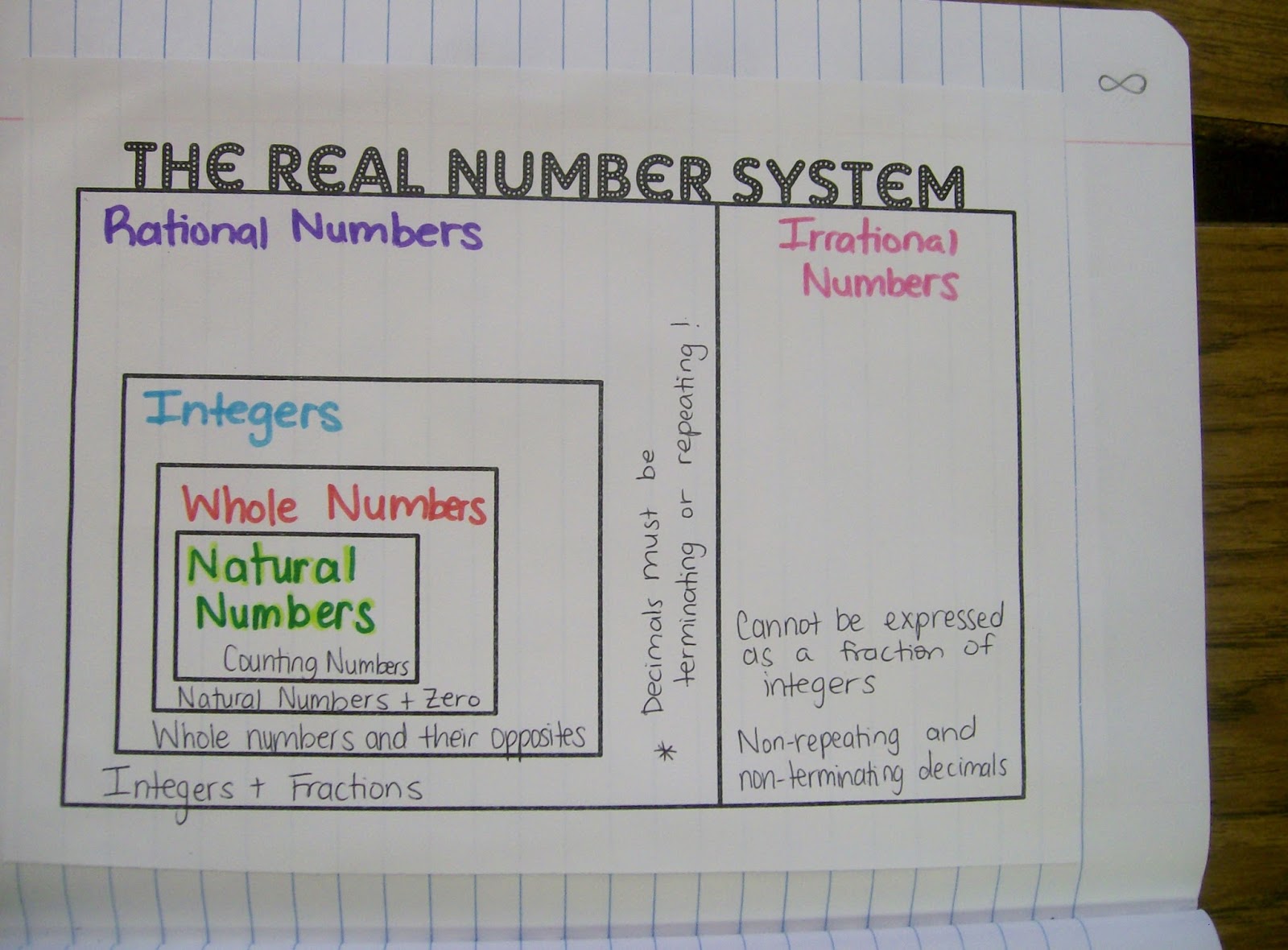
I ended up creating another version of the real number system graphic organizer.
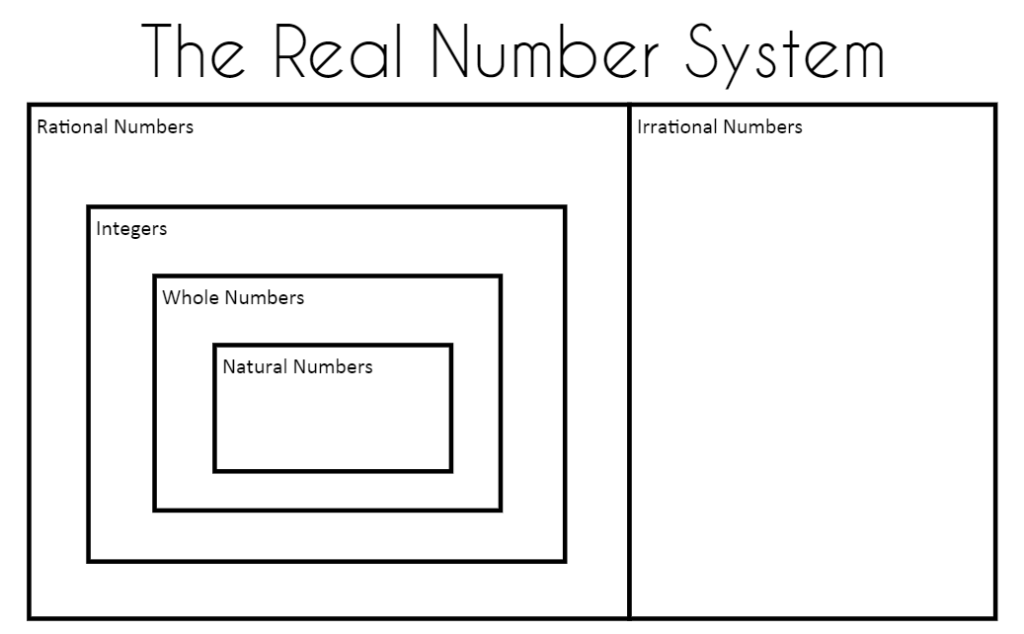
Free Download of Real Number System Graphic Organizer
Real Number System Graphic Organizer (PDF) (8034 downloads )
Real Number System Graphic Organizer 2.0 (PDF) (5748 downloads )
Real Number System Graphic Organizer 2.0 (Editable Publisher File ZIP) (3379 downloads )
Free Download of Frayer Models (6 to a Page)
You might also be interested in a graphic organizer I created for the subsets of the real numbers.
More Activities for Teaching the Real Number System
- Real Number System Activities
- Real Number System Card Activity
- Always Sometimes Never Dice Activity for Real Number System
- Rational and Irrational Numbers Exploration Activity
- Real Number System Nesting Boxes
- Real Number Line Project
- Subsets of the Real Numbers Graphic Organizer
- Properties of Real Numbers Foldable
- Properties of Real Numbers Graphic Organizer
- Real Number System Graphic Organizer
















So nice looking! What if you coordinated the frayer model to the color it is being outlined in on the graphic organizer?
I just wanted to make sure you are aware that your recent efforts are very much appreciated; I'm constantly starring your posts in Google Reader (subscribed to 150+ math/science ed blogs) as quality stuff I want to be able to refer to again later. The nested set diagram may be fairly standard, but your overall presentation of the real number system in the INB is something I plan to mimic during the first week or two of school!
Thank you so much! I feel like I've stolen so many ideas from other teachers for so long. It feels good to create something of my own and share it with the world. 🙂
I thought I saw a link to where you have the frayer model template that you are using, but now I can't seem to locate it. We would love to use this for our INBs this year! Thanks for you help! ~Laura
thats was a great organizer…
btw i want to share about irrational number
https://web.archive.org/web/20110610052612/http://www.math-worksheets.co.uk:80/048-tmd-what-are-irrational-numbers/
I have one slight problem with this though…the square root of 25 is 5 or -5 which means that it would be an integer and NOT a Whole Number, plus 6 and 4/2 should also be natural numbers…the only number that you can really put in whole numbers that isn't a natural number is zero.
If the sign is not given in front of the radical sign, then the answer is the principle root, which is positive. When you have a quadratic equation to solve and you need to take the square root of the number, then you use both roots…5 and -5.
If you notice the way this is set up, natural numbers are a subset of whole, integers, and rational numbers. Whole numbers are a subset of integers and whole numbers. When you look at it that way the square root of 25 is both a whole number AND an integer.
Actually it would be a natural number not a whole number AND an integer if you want to put it in two places, the ONLY number that can strictly be put in whole numbers is zero because every other whole number is Natural.
It is my understanding……
Square root of 25 is the principal root only, 5. We only include the -5 as a solution to square root 25 when you are solving for a variable….x^2 = 25….then square root x = square root 25, which then has two answers, 5 or -5.
I am unable to find the second page of your interactive notebook. I would like the page that has the foldable for vocabulary and examples. I love this! Thanks for your help.
So would I…
🙂
Great visuals. I teach 6th and have had some trouble using the Frayer models. The kids always have a really hard time with the Facts & Characteristics box. (And honestly, I do too…should I be admitting that?) Anyway, I wondered if you would share a pic of the inside of any of these models. Thanks! s.woodruff@snet.net
I so love this thank you!!!
You're welcome!
I absolutely love you! Thank you so much for sharing all your great resources.
You're very welcome, Kelly!
You are inspiring. I
Thanks!