Weird Analogies: The Halloween Candy Tax
This blog post contains Amazon affiliate links. As an Amazon Associate, I earn a small commission from qualifying purchases.
Want to check out my favorite Amazon items for the classroom? Check out my Amazon favorites page!
If you spend much time in my classroom at all, you will quickly realize that I use lots of weird analogies. Some analogies I use once and forget about. Other times I start analogies without really thinking about them and end up regretting my decision. And, sometimes, my analogies actually work and I end up being able to use them more than once.

I don’t remember the first time I used this analogy, but I think it must have been during my first year of teaching. My students were struggling with factoring the GCF out of an expression. We were looking at problems like this:
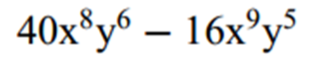
It didn’t take much convincing that we should factor an 8 out of both terms. But, my students were insistent that we could only factor out one x and one y. Once I convinced them that it was okay to factor out more than a single variable, many of them defaulted to wanting to factor out the number of variables from the first term. So, in this example, they would want to factor out x to the eighth and y to the sixth. Telling them that we wanted to factor out the greatest number of things they had in common didn’t really seem to help.

So, today, the class is confused. Frustrated. Ready to give up. Fixed mindset statements are being uttered at every turn. And, I’m pretty sure most of my students would describe themselves as being in the panic zone. I sit on top of an empty student desk, and I look around at my students. Eventually they seem to sense that I have something to say:
Okay, everyone. Listen up. From walking around and listening to your conversations, I can tell that we’re struggling. I’m going to tell you a story. Maybe it will help. Maybe it won’t. Maybe you’ll go home tonight and tell your parents what a crazy math teacher you have. But, maybe, just maybe, it will help to shed some light on the problems we’ve been attempting to work.
Some day you will have children. [This statement usually gets their attention!] And, every year you and your children will participate in this crazy tradition. October will roll around, and you will dress up your little ones in adorable or spooky costumes. Then, you’ll go from door to door with cute, colorful pumpkin pails. The simple act of uttering three little words will result in candy being placed in your kids’ pails. After visiting a number of houses, pumpkin pails will be overflowing, and you and your children will return home, excited to sort through the candy that has been amassed.
At this point, you explain to your children that there are certain things in life that…well…may not seem fair. But, life goes on, and things like taxes must be paid. To help your children learn about the tax system, a Halloween Candy Tax (HCT) will be applied to the night’s acquisitions. But, your children needn’t worry too much because you will be very fair in collecting the tax.
The HCT requires that the candy must first be sorted by type. Tootsie Rolls are placed with Tootsie Rolls. Butterfingers with Butterfingers. Twizzlers with Twizzlers. I think you get the idea. The main idea behind the tax is that the same number of each kind of candy will be taken from each of your children. If one child has 5 lollipops and and your other child has 7 lollipops, the most lollipops you can take will be 5 lollipops because that is the most that you can take from BOTH of your children. And, because you are greedy and jealous that you are now definitely too old to go trick or treating yourself, you will always take the greatest possible number of candies from all of your children. Sure, you could just take two lollipops from each child, but your greed will cause you to take 5 lollipops from both children.
[At this point in the story, my students are outraged. The one poor child now has zero lollipops. Insert lots of comments about the injustice of the situation and what a terrible person I am. My hope is that if they’re engaged in the story, they’ll be engaged in how it relates to the problem we’re trying to solve.]
Imagine you have two kids. Billy and Sally.
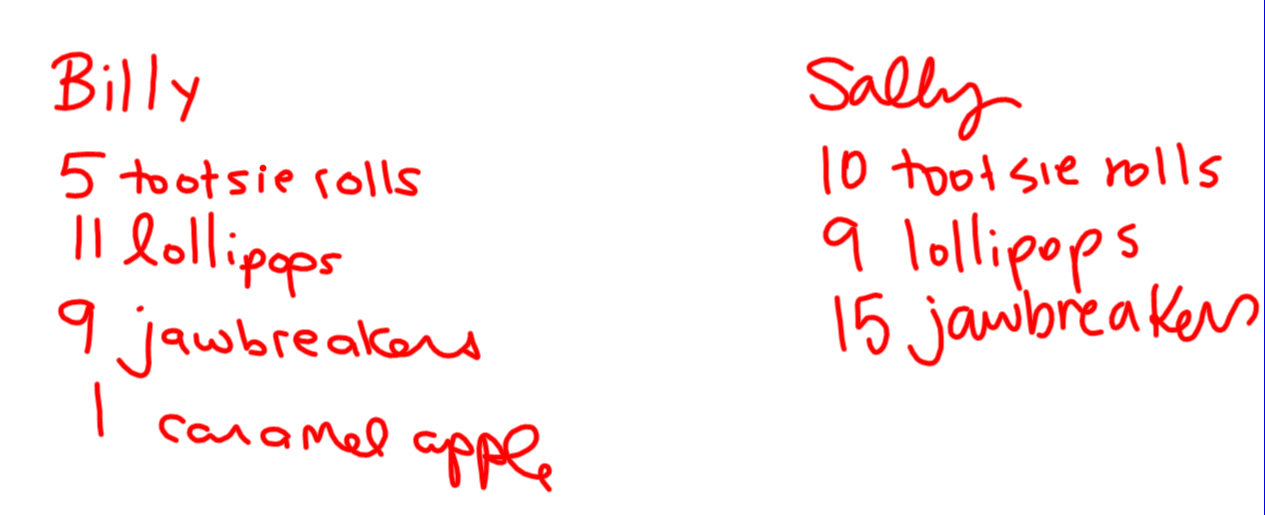
Billy and Sally dump out their pumpkin pails to find tootsie rolls, lollipops, jawbreakers, and a caramel apple. How many tootsie rolls will you tax your children if you want to be fair but greedy? What about lollipops? Jawbreakers? What about that lone caramel apple? Who gets it?
Eventually, you end up with this:
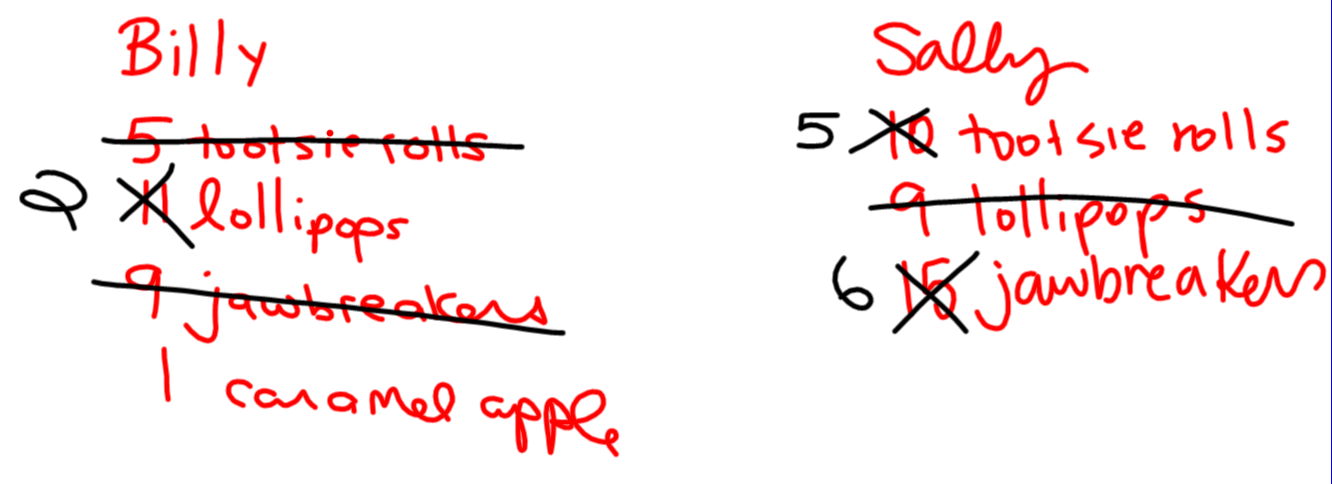
The class decides that Billy really didn’t end up well in this deal. Of course, they word it a bit more crudely than that.
Back to the problem:
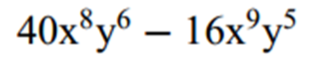
We decide to let the x’s represent starbursts and the y’s represent smarties. If one child has 8 starburts and the other child has 9 starbursts, a greedy but fair parent will take 8 starbursts from each child. And, the maximum number of smarties that can be taken from both children would be 5. All of a sudden, lightbulbs start to come on. Why didn’t you explain it this way in the first place?
Does every student need this analogy? I don’t think so. Students who already understand the concept of finding the GCF will likely find the story annoying and pointless. Why would you need to think about Halloween candy? But, I’ve found that this analogy makes factoring a bit more tangible for my students who have traditionally struggled with math.
And, for the record, I don’t tax my own children’s Halloween candy. I’d kinda need children to be able to do that. And, according to my students, this would be a totally unfair policy. So, I guess when I do have kids of my own one day, I’ll just have to buy my own Halloween candy…
More Activities for Teaching Polynomials
- X Puzzles Factoring Review Game
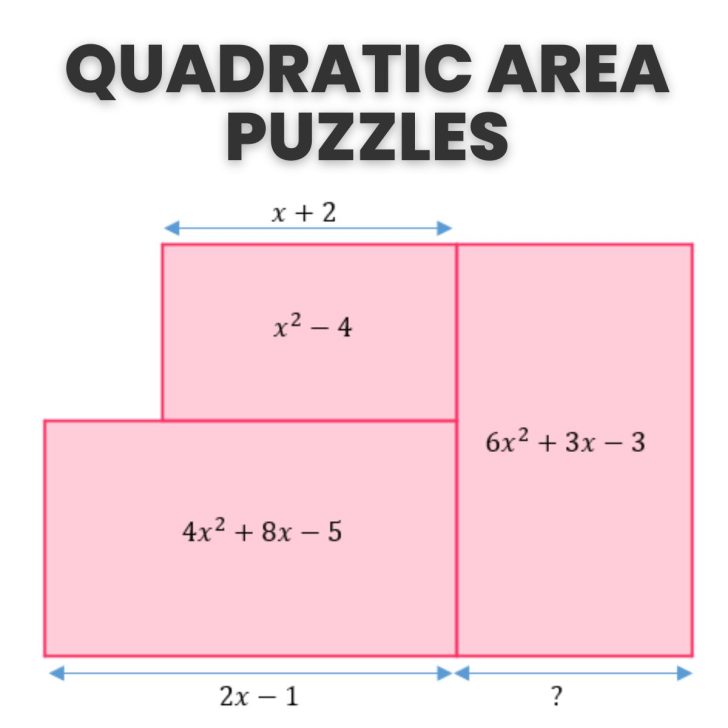
- Quadratic Area Puzzles
- Shared Factors – A Quadratics Puzzle
- Naming Polynomials Poster
- “Polly”nomial
- Naming Polynomials Speed Dating Activity
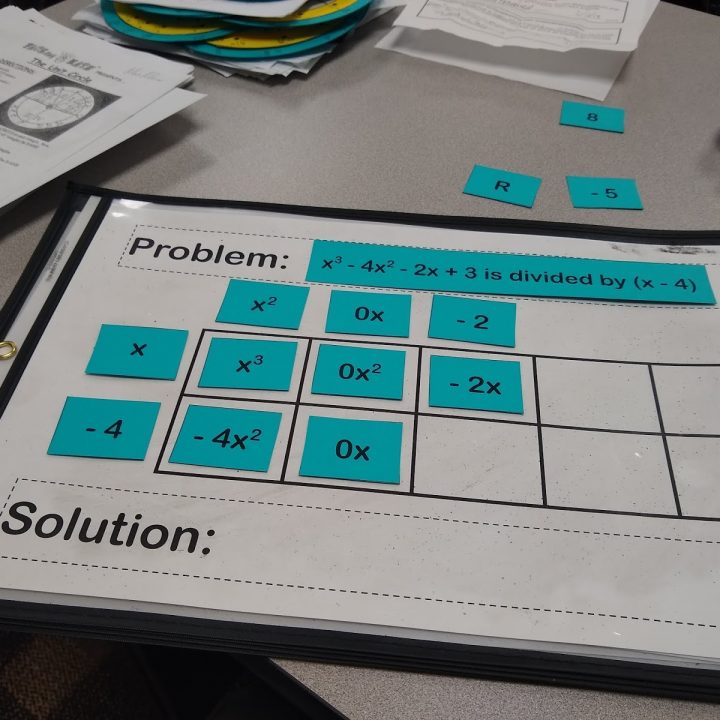
- Dividing Polynomials Using the Box Method Puzzles
- Area Model Puzzles from Christie Bradshaw
- Adding and Subtracting Polynomials Graphic Organizer
- Writing Polynomials in Standard Form Foldable
- Factoring Quadratics Foldable
- Multiplying Polynomials Foldable
- Naming Polynomials Practice Sheet
- Polynomial or Not Color Coding Activity
- Polynomial Frayer Model Template
- Roots Solutions Zeros X-Intercepts Posters
- Multiplying Polynomials Egg Hunt Activity
- Human Polynomials Activity
- Introducing Algebra Tiles to Students
- Building and Naming Polynomials Activity
- Factoring Trinomials with GCFs Question Stack Activity
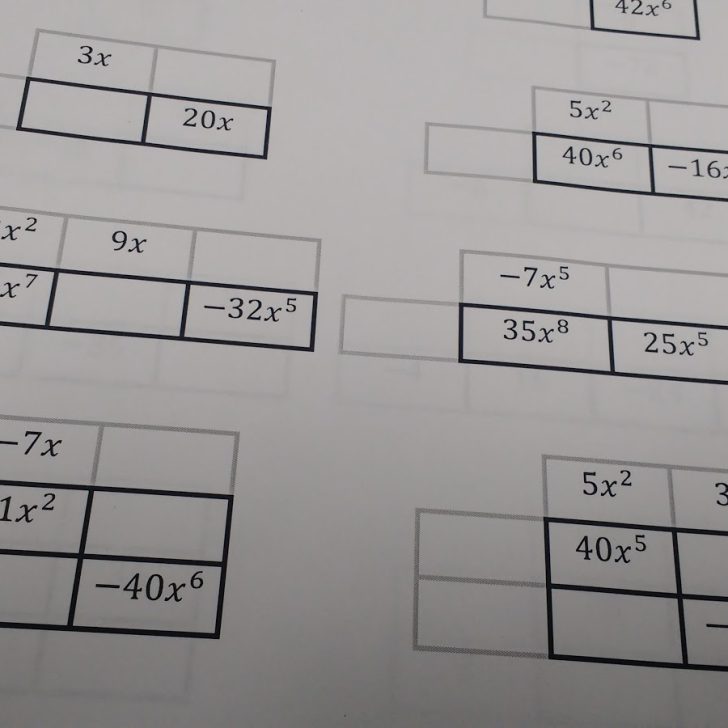
- Factoring Polynomials Using the Box Method Directions
- Looking for Patterns in Factoring Quadratics
- Factoring Quadratics Question Stack Activity
- Dividing Polynomials Using the Box Method Activity
- Dividing Polynomials Using the Box Method Foldable
- Multiplying Polynomials Using the Box Method Foldable
- Adding and Subtracting Polynomials Notes
- Parts of a Polynomial Practice Book
- Standard Form of a Polynomial Interactive Notebook Page
- Factoring out the GCF of a Polynomial Foldable
- Factoring vs Distributing Card Sort Activity
- Factoring Quadratics Using the Box Method Foldable
- Naming Polynomials Graphic Organizer
- Factoring Quadratics Graphic Organizers
- Adding and Subtracting Polynomials Activity






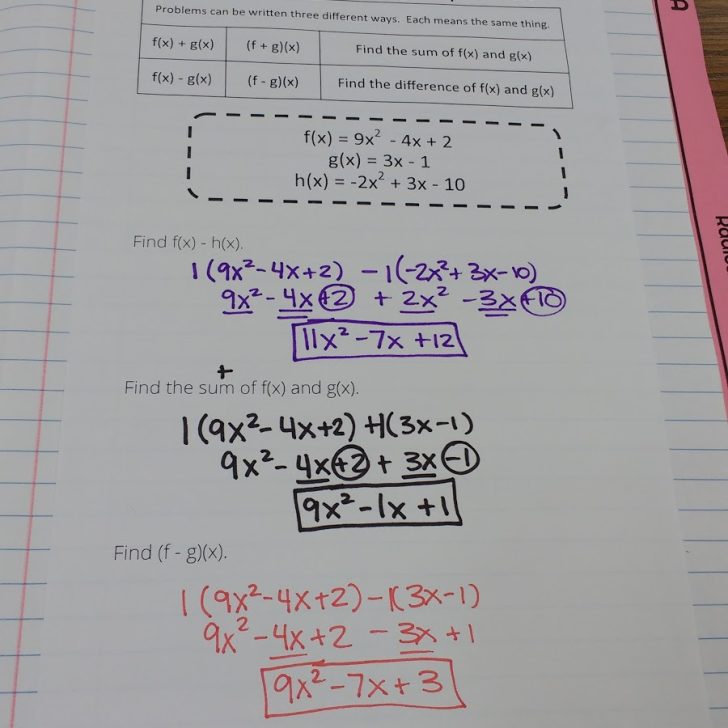

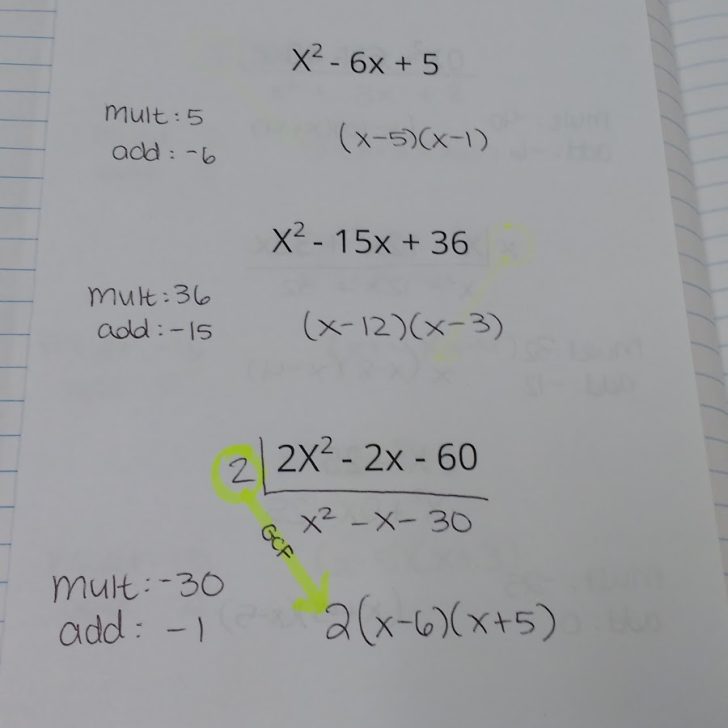

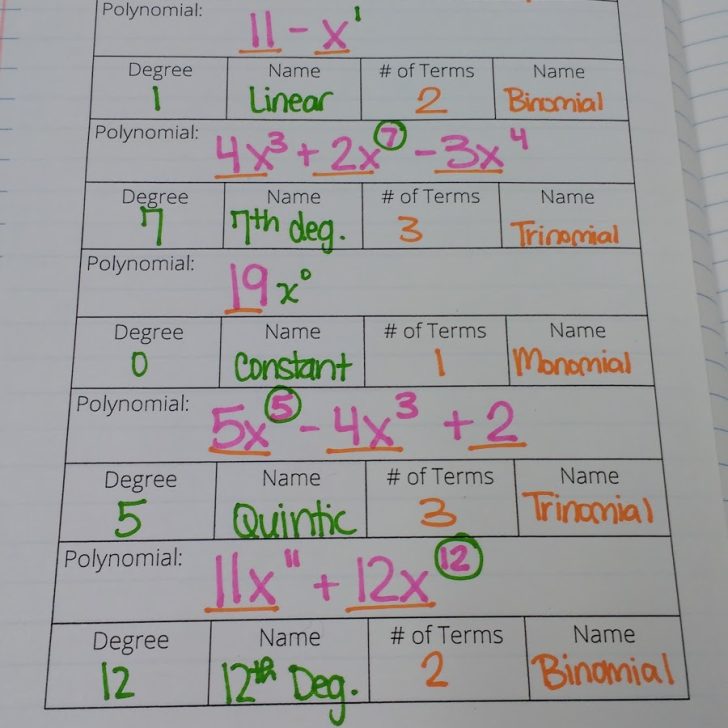








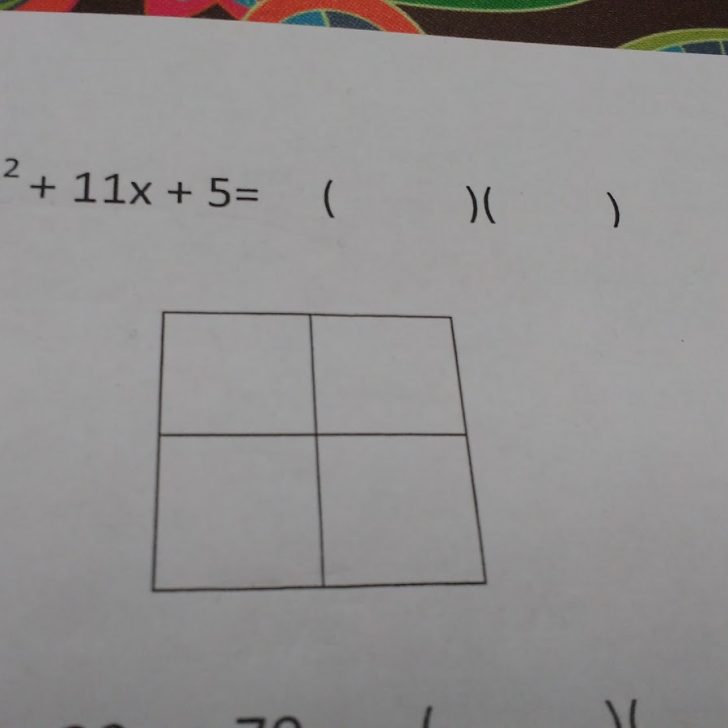



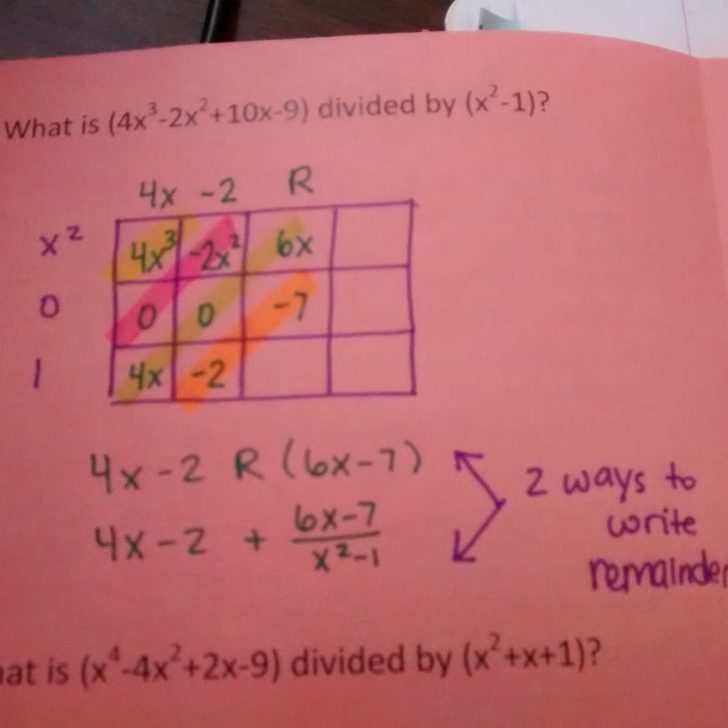












Thanks so much for the post! I'm actually just about up to factoring with my algebra II class and after our winter vacation we're going to be looking at GCF. Thanks for the analogy! I don't know if I'll need it, but if I do, I have it in my back pocket!
Good luck! Teaching factoring the GCF can be tough. Hope it went well!
Great analogy! It gives students a concrete mental picture to go with the variables.
Thanks Nancy!
Nice, Sarah. Concrete analogies to somewhat abstract mathematical concepts are very useful. Adding this one to the toolbox.
Thanks Brian!