Dividing Polynomials Using the Box Method Foldable
I want to share this dividing polynomials using the box method foldable that I created for my Algebra 2 students to work through and glue in their interactive notebooks.
I’m excited to talk about one of my favorite things in the world with you here on my blog: dividing polynomials.

I used to dread teaching dividing polynomials because it meant teaching polynomial long division. My Algebra 2 students couldn’t even remember how to do regular long division.
As a high school student, I remember being taught synthetic division, but that method only works if the polynomial you are dividing by meets certain requirements.
Then, my teaching life was changed when I was introduced to the box method.
If you’re not familiar with the box method, you should probably start with this post on multiplying polynomials.
Here’s the steps I wrote out for my students in case they forgot the process. They’re not perfect. But, considering the fact that I didn’t give my students any written out steps last year, they are a vast improvement over nothing. Feel free to tweak them and make them better!

Then, we did four example problems together. The kids gave me grief for not printing this on white copy paper. Apparently peach paper and highlighting don’t go well together. Note to self: use white paper next year!
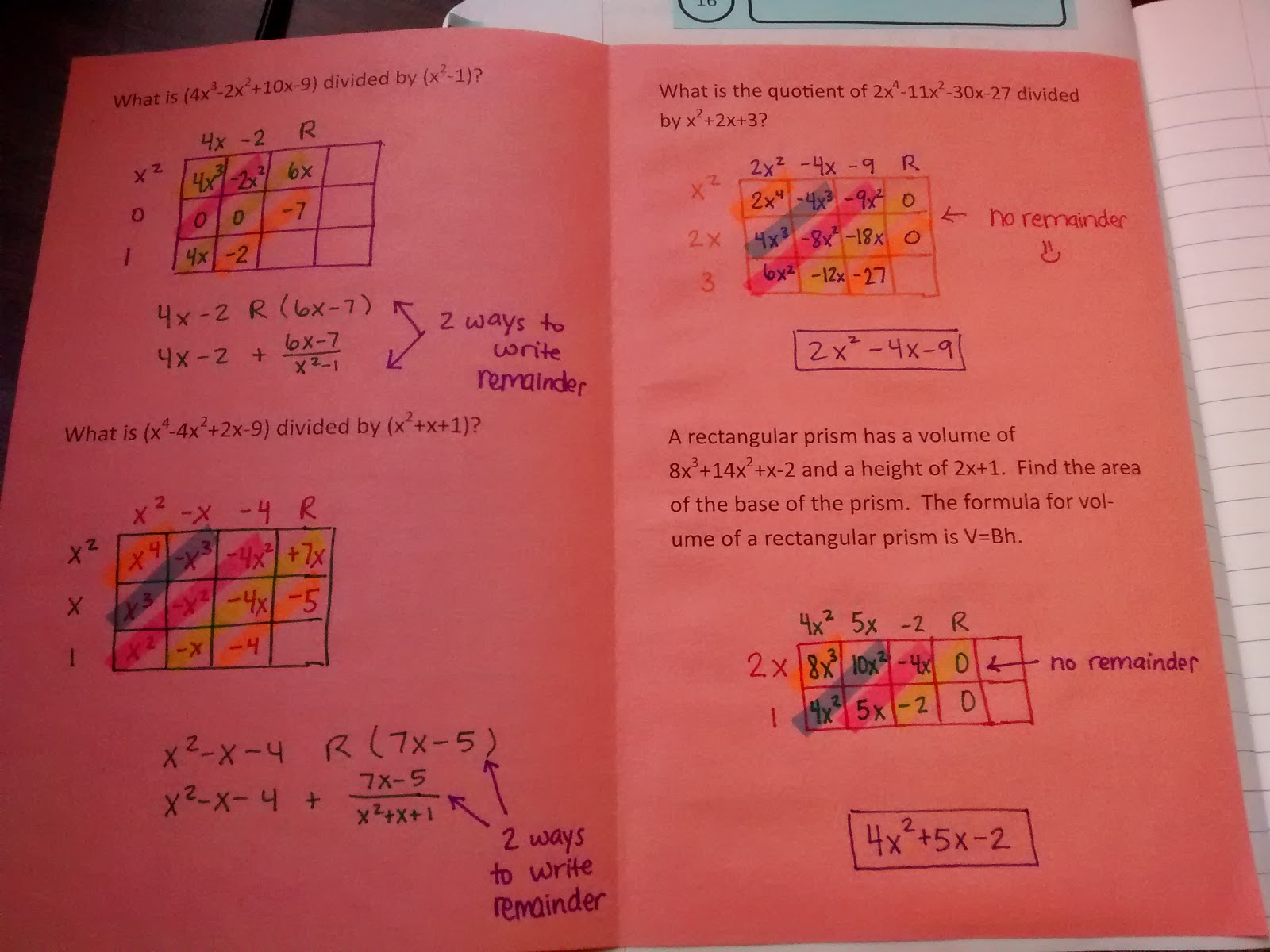
And, here’s a close-up of each problem.

I made sure I gave them two problems with remainders and two without.
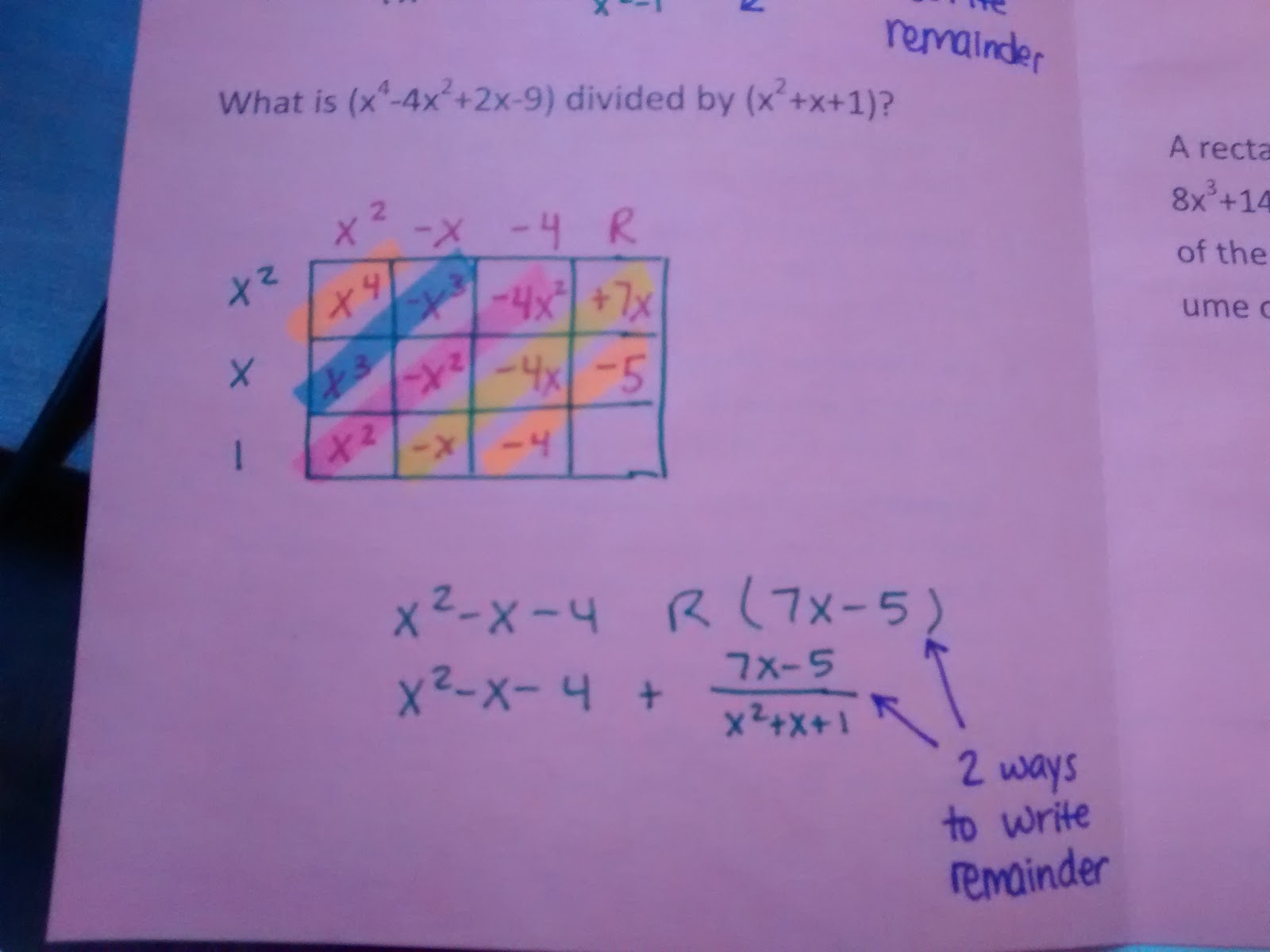
See how I have them write an R in the space following the constant in the answer? This is a trick I learned from a student last year. She invented that strategy on her own.
As soon as I saw it, I knew I was going to steal it and implement it the next year. I did, and I’m so glad I did!
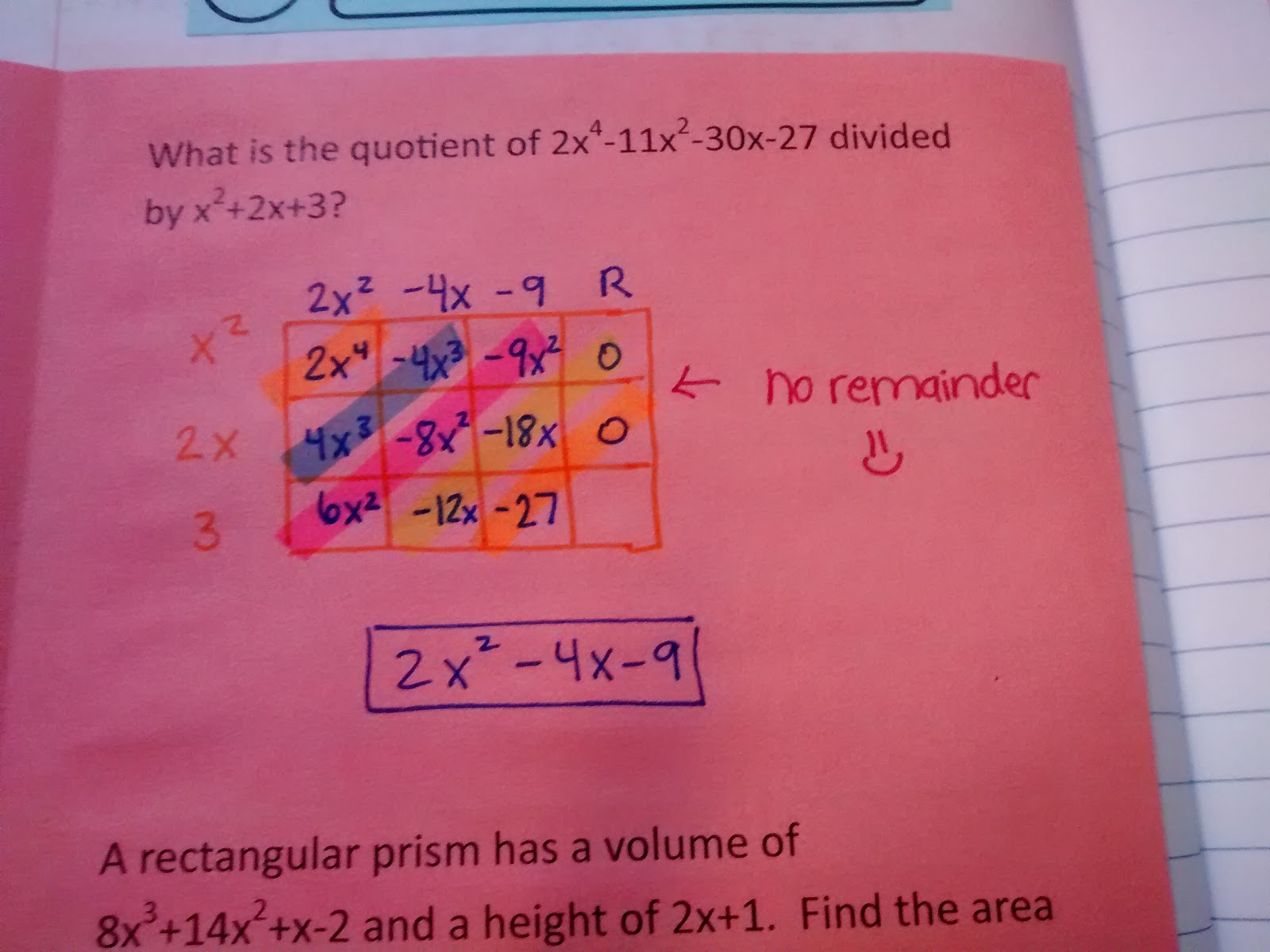
I also made sure I exposed to them to an “application” problem that they might see on their end-of-instruction exam.
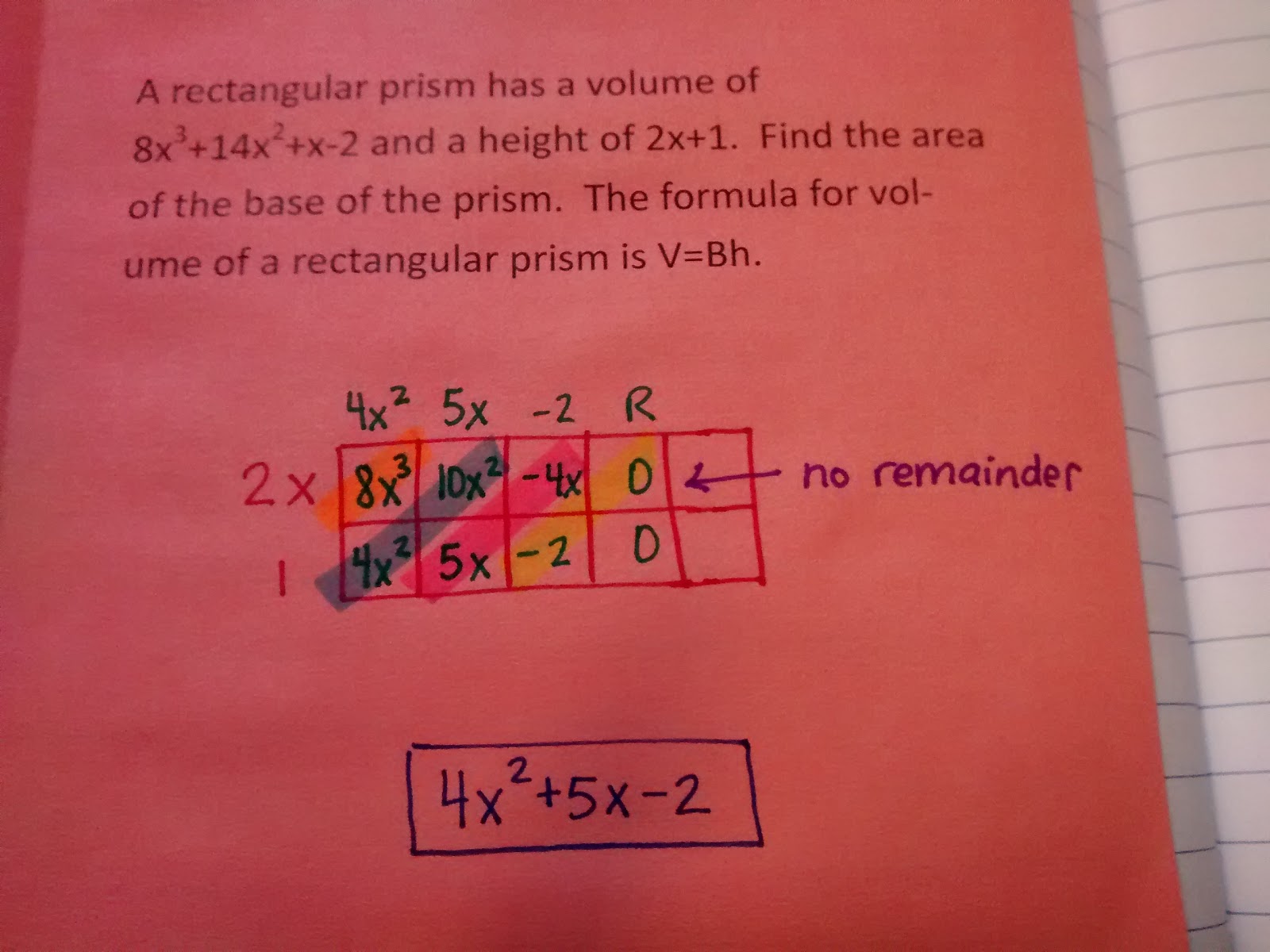
After doing 4 example problems together, I could tell that they were really frustrated. I tried explaining that this was the easy method. But, they didn’t believe me. So, I decided to devise some dividing polynomial jigsaw puzzles for my students to put together.
Free Download of Dividing Polynomials Using the Box Method Foldable
Box Method for Dividing Polynomials Foldable (PDF) (1216 downloads )
Box Method for Dividing Polynomials Foldable (Editable Publisher File ZIP) (889 downloads )
More Activities for Teaching Polynomials
- X Puzzles Factoring Review Game
- Quadratic Area Puzzles
- Shared Factors – A Quadratics Puzzle
- Naming Polynomials Poster
- “Polly”nomial
- Naming Polynomials Speed Dating Activity
- Dividing Polynomials Using the Box Method Puzzles
- Area Model Puzzles from Christie Bradshaw
- Adding and Subtracting Polynomials Graphic Organizer
- Writing Polynomials in Standard Form Foldable
- Factoring Quadratics Foldable
- Multiplying Polynomials Foldable
- Naming Polynomials Practice Sheet
- Polynomial or Not Color Coding Activity
- Polynomial Frayer Model Template
- Roots Solutions Zeros X-Intercepts Posters
- Multiplying Polynomials Egg Hunt Activity
- Human Polynomials Activity
- Introducing Algebra Tiles to Students
- Building and Naming Polynomials Activity
- Factoring Trinomials with GCFs Question Stack Activity
- Factoring Polynomials Using the Box Method Directions
- Looking for Patterns in Factoring Quadratics
- Factoring Quadratics Question Stack Activity
- Dividing Polynomials Using the Box Method Activity
- Dividing Polynomials Using the Box Method Foldable
- Multiplying Polynomials Using the Box Method Foldable
- Adding and Subtracting Polynomials Notes
- Parts of a Polynomial Practice Book
- Standard Form of a Polynomial Interactive Notebook Page
- Factoring out the GCF of a Polynomial Foldable
- Factoring vs Distributing Card Sort Activity
- Factoring Quadratics Using the Box Method Foldable
- Naming Polynomials Graphic Organizer
- Factoring Quadratics Graphic Organizers
- Adding and Subtracting Polynomials Activity






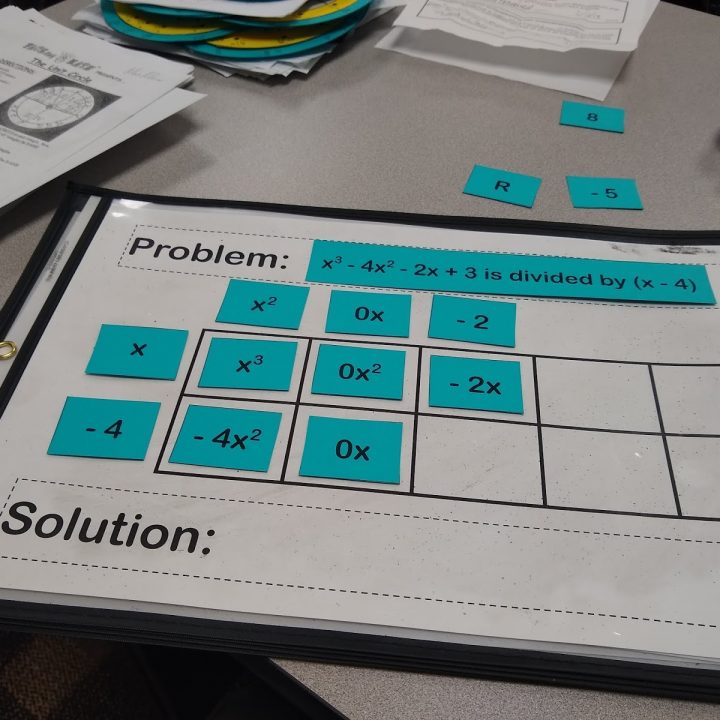

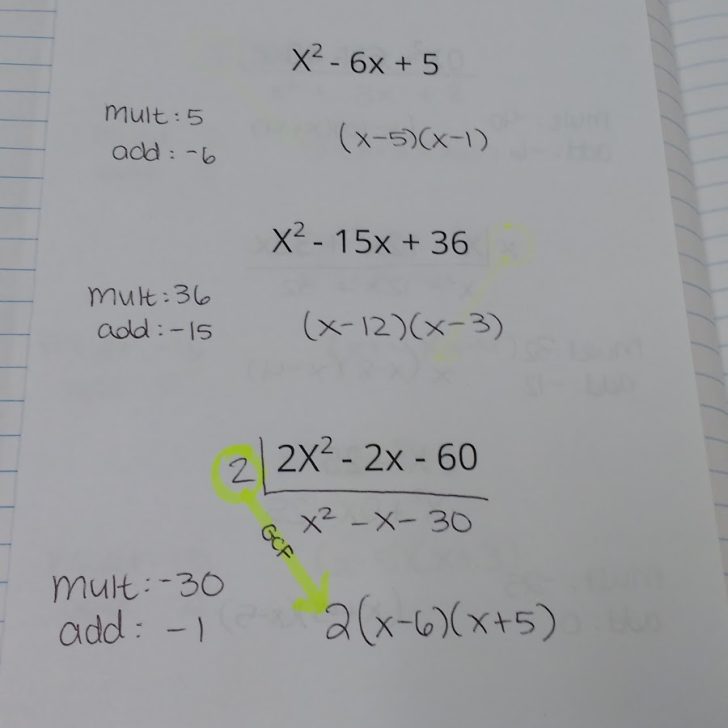

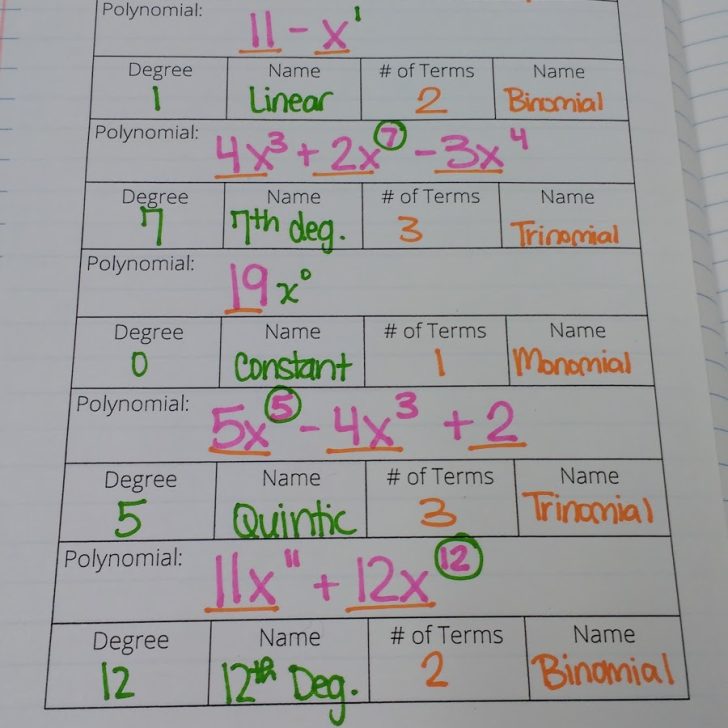











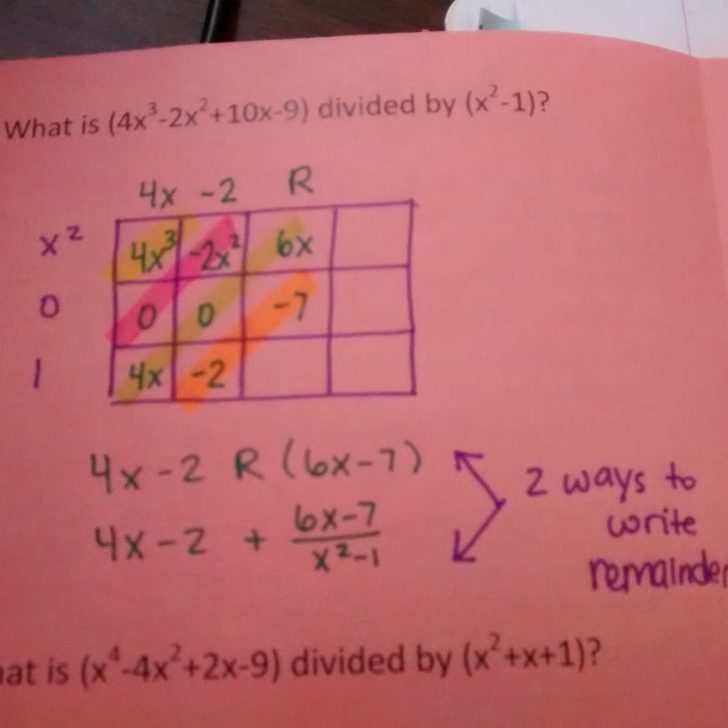












you could also not use the index cards for anything except the original problem and have them use expo makers (for ones that don't need cards). Expo wipes off desks incredibly easily.
Great idea!
Ahh – thank you for the step-by-step photos!
Actually… I had an Algebra 2 student transfer to my school in Missouri last year, and one day I was looking for some foldables on your website, not realizing that your blog was showing on the Smartboard. As I scrolled and your picture showed, the student said, "Hey, that's my teacher from Oklahoma!" My students made fun of me for the entire year because I went crazy telling him about how his previous math teacher is a famous blogger 🙂
Anyway, he showed me the box method that you taught toward the end of the year, but I didn't take the time to really get to know it well enough to teach it. Now I know! Thank you!! And thanks for everything you do – your blog has inspired me to do so much more in my classroom!
That is too crazy!
Thank you for this! I love it. What great low-tech ideas. I have always struggled with finding a creative way to get students to understand this concept. It's a dry topic, and these strategies give it life!
I had the students make Google Slide presentations showing the step-by-step process for solving.
Thanks for sharing!
I like that idea!
On the problem on the top left of the notes, along the left side of the box you put a positive one at the bottom and the problem says negative one? Do you always change the sign?
I was wondering the same thing. Looking at the other examples, to me, it should be a negative one on the side – which changes many of the boxes and the remainder.
First, I must say, you are amazing.
Second, thank you for sharing your lessons. I am using your posts for past 3 years.
Third, THANK YOU again!
P.S. Your post “Dividing Polynomials Using the Box Method” has a mistake in first example. It starts in first column last row: 4x times -1 is -4x and it continues in second column last row: -2 times -1 is 2. Which changes the remainder to 14x-11.
Thanks for catching my mistake, and thanks for reading my blog!